倍增算法讲解 + 例题：AcWing 1273. 天才的记忆（RMQ问题的ST算法）

倍增，意思就是 “成倍增长”。

在进行递推时，如果 状态空间很大，通常的 线性递推 无法满足时间与 空间复杂度 的要求，那么我们可以通过 成倍增长 的方式，只递推 状态空间 中在 2 的整数次幂位置上的值 作为代表。

当需要 其他位置上 的值时，我们通过 “任意整数可以表示成若干个 2 的次幂项的和” 这一性质，使用 之前求出的代表值 拼成 所需的值。

所以使用 倍增算法 的一个基本要求：递推问题 的状态空间 关于 2 的次幂 具有 可划分性。

“倍增” 与 “二进制划分” 两个思想 互相结合，降低了求解很多问题的时间与 空间复杂度。

之前学习的 快速幂 其实就是 “倍增” 与 “二进制划分” 思想的一种体现。

在本篇中，我们研究 序列上的倍增问题，包括 求解RMQ(区间最值）问题 的 ST算法。

关于 求解最近公共祖先（LCA）等在树上的倍增应用，将在后续进行分析。

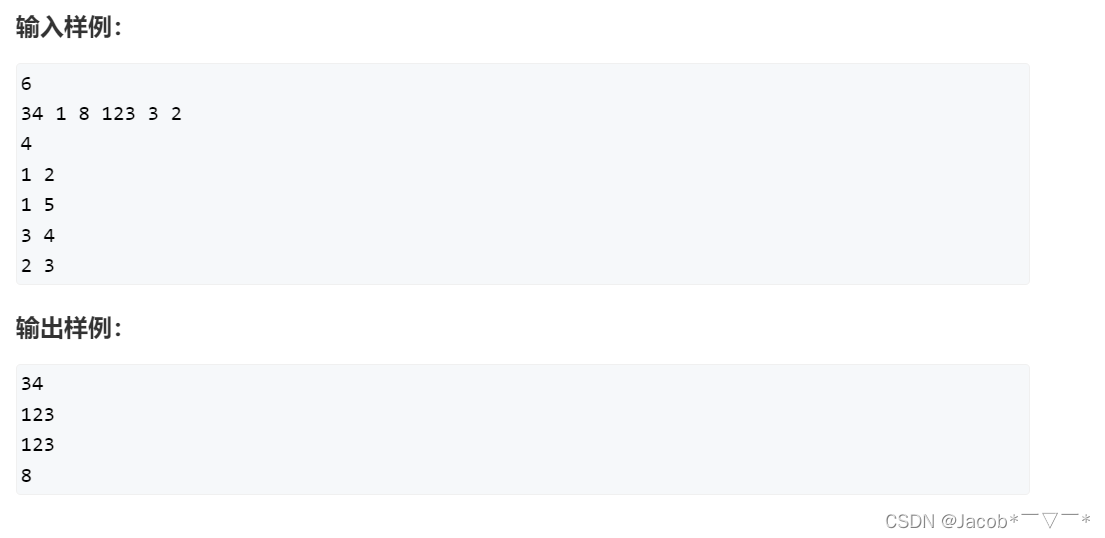
在这里插入图片描述

题意：

给定一长串数列，发出一系列询问：区间 [l，r] 中的 最大值，并输出结果。

数列中 素个数范围<=2e5，询问个数<=1e4，显然不可以暴力求解。

思路：

对于这种 询问区间最大值 问题，当然做法可以有多种，比如之前探讨过的线段树，

不过本题如果用线段树求解，其代码不免显得过于冗长了，

对于此类问题我们有一个专门的应对利器，那就是 RMQ算法（用于解决 区间最大值问题），其 代码短小，而且常用。

首先要明确的一点是：RMQ算法 其本质其实是 动态规划，它还有其它的称谓：ST表、跳表。

其 总体思想 就是：先 倍增预处理，之后进行 快速查询。（缺点：是一个 静态算法，不支持修改）

接下来进行 dp分析：

`f[i, j]`状态表示：

从 i 开始，且长度为 2 ^ j 的区间中最大值是多少。

举个例子就很清晰了，

求 区间 [i, j] 中的最大值，显然可以将此区间均分为 左右两区间，答案显然为 从两半区间的最大值之中取 max 。

对于 左半边区间，根据定义可得：f[i, j - 1]，右半边也易得：f[i + 2 ^ (j - 1), j - 1]。

最终得到 状态转移方程：f[i, j] = max(f[i, j - 1], f[i + 2 ^ (j - 1), j - 1])。（f[i][j] = max(f[i][j-1], f[i+(1<<(j-1))][j-1]);）

查询：

对于查询 区间 [l, r] 中 的 最大值，设区间 [l, r] 的长度为 len，先找到 <=len 的 2 的最大整次幂 k，意味着，2 * 2 ^ k 一定 满足 > len，因此 严格覆盖整段 [l, r] 区间最多需要两段长度为 2 ^ k 的区间。

因此对于 查询区间 [l, r] 中的最大值，我们可以 分为两部分最大值取 max 进行分析：

从 l 开始，长度为 2 ^ k 的区间最大值：f[l, k]
从 r - 2 ^ k + 1 开始，长度为 2 ^ k 的区间最大值：f[r - 2 ^ k + 1, k]

以O(1)的时间复杂度 进行查询：max(f[l, k], f[r - 2 ^ k + 1, k])。（max(f[l][k], f[r - (1 << k) + 1][k]);）

对于上面说到的 k ，我们也可以进行 预处理，或者 直接使用 math库函数log(x)（此函数 以10为底），由于 k = log(2, len)（向下取整），根据 换底公式 可得 log(2, len) = log(10, len) / log(10, 2)（向下取整）

时间复杂度：

O(nlogn + q)

代码：

#include<bits/stdc++.h> using namespace std; const int N = 2e5+10, M = 18; int n, q; int a[N]; int st[N][M]; void init() { for(int j=0; j<M; ++j) { for(int i=1; i+(1<<j)-1<=n; ++i) { if(!j) st[i][j] = a[i];//当区间长度为 1 的时候直接赋值 else st[i][j] = max(st[i][j-1], st[i+(1<<(j-1))][j-1]); } } } int ask(int l, int r) { int len = r - l + 1; int k = log(len) / log(2); return max(st[l][k], st[r - (1 << k) + 1][k]); } int main() { cin>>n; for(int i=1; i<=n; ++i) scanf("%d", &a[i]); init(); cin>>q; while(q--) { int l, r; scanf("%d%d", &l, &r); printf("%d\n", ask(l, r)); } return 0; }

关于 st表，我最近在牛客上做了一道好题，详情请戳炸鸡块君与FIFA22。

今天的文章倍增算法讲解 + 例题：AcWing 1273. 天才的记忆（RMQ问题的ST算法）分享到此就结束了，感谢您的阅读。

倍增算法讲解 + 例题：AcWing 1273. 天才的记忆（RMQ问题的ST算法）

题意：

思路：

f[i, j]状态表示：

查询：

时间复杂度：

代码：

相关推荐

`f[i, j]`状态表示：