DECL

DECL结构是比较通用的来表示几何的数据结构
主要包括三种数据结构：
1.点 vertex
2.半边 edge
3.面 face

点

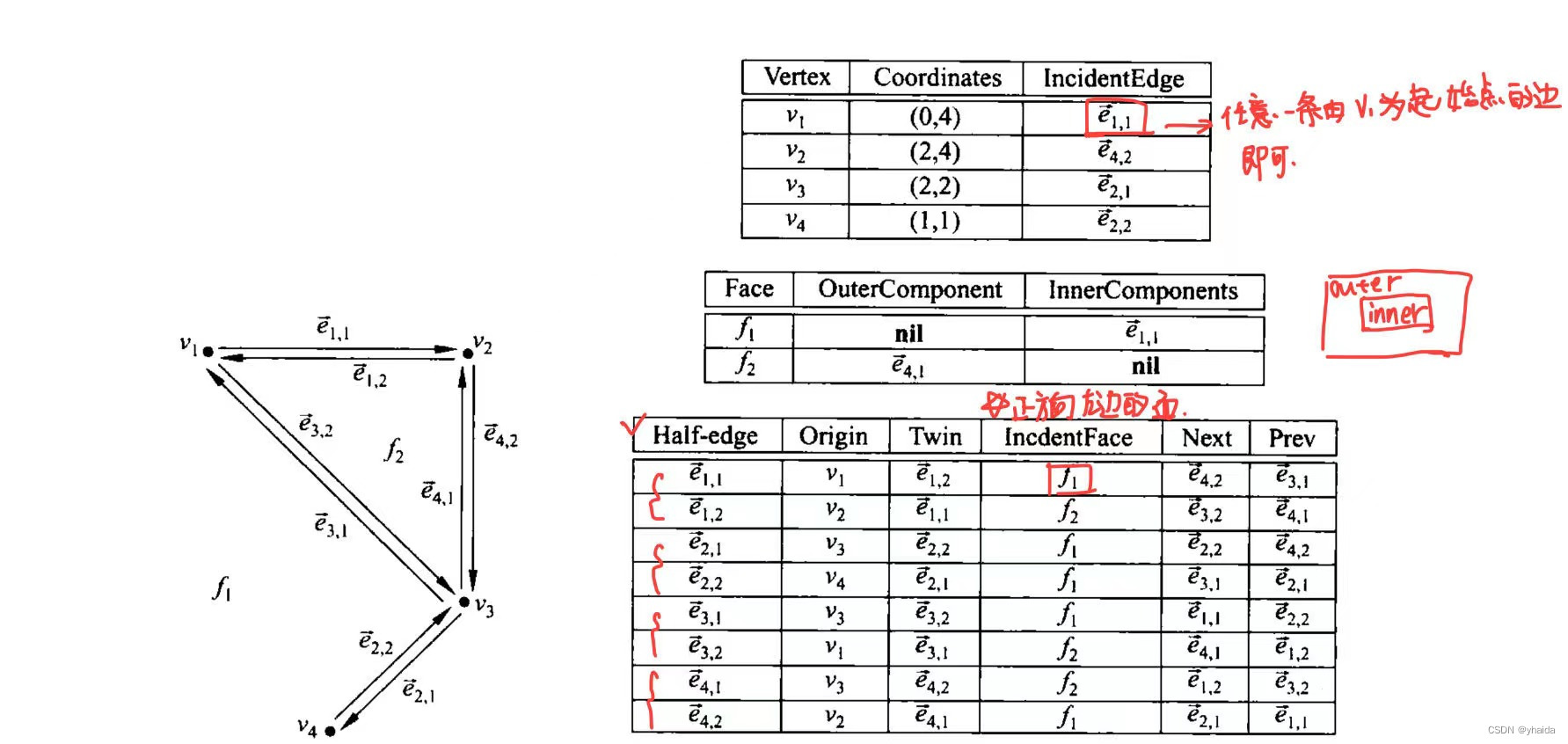
存储点的位置以及任意一条由该点为起点向量的半边

半边

其中几何边由两条半边组成

这也是一种表示方式

面

存储一个面的外边界和内边界，如果外边界或者内边界不存在那么直接等于nullptr

像下面这种情况内部空洞需要用一个vector来存储了

通用的表达方式

数据结构简单实现（不包括具体操作）

template<typename type = float, size_t dim = DIM3> struct VertexDCEL { 
    Vector<float, dim> point;// 1.Coordinates EdgeDCEL<type, dim>* incident_edge = nullptr;// 2.以point任意为起点的半边 VertexDCEL(Vector<type, dim>& _point) :point(_point) { 
   } //...... }; template<typename type = float, size_t dim = DIM3> struct EdgeDCEL { 
    //1.起始点 VertexDCEL<type, dim>* origin = nullptr; //2.与该半边相关联的三条半边 EdgeDCEL<type, dim>* twin = nullptr; EdgeDCEL<type, dim>* next = nullptr; EdgeDCEL<type, dim>* prev = nullptr; //3.该半边对应的面 FaceDCEL<type, dim>* incident_face = nullptr; int id = -1; EdgeDCEL() :id(-1) { 
   } EdgeDCEL(VertexDCEL<type, dim>* _origin) :origin(_origin) { 
    id++; } VertexDCEL<type, dim>* destination() { 
    return twin->origin; } //...... }; template<typename type = float, size_t dim = DIM3> struct FaceDCEL { 
    EdgeDCEL<type, dim>* outer = nullptr; std::vector< EdgeDCEL<type, dim>*>inner;//可能会有空洞 void print()//只输出外边界 { 
    if (outer) { 
    auto edge_ptr = outer; auto next_ptr = outer->next; edge_ptr->origin->print(); while (next_ptr != edge_ptr) { 
    next_ptr->origin->print(); next_ptr = next_ptr->next; } } } //...... }; template<typename type, size_t dim = DIM3> class PolygonDCEL { 
    typedef Vector<type, dim> VetorNf; std::vector< VertexDCEL<type, dim>* > vertex_list; std::vector< EdgeDCEL<type, dim>* > edge_list; std::vector< FaceDCEL<type, dim>* > face_list; //保存空的边，没有组成面->边集合 EdgeDCEL<type, dim>* empty_edge = new EdgeDCEL<type, dim>(); public: explicit PolygonDCEL(std::vector< VetorNf>&); bool split(VertexDCEL<type, dim>* _v1, VertexDCEL<type, dim>* _v2); bool join(VertexDCEL<type, dim>* _v1, VertexDCEL<type, dim>* _v2); std::vector<VertexDCEL<type, dim>*> getVertexList(); std::vector<FaceDCEL<type, dim>*> getFaceList(); std::vector<EdgeDCEL<type, dim>*> getEdgeList(); VertexDCEL<type, dim>* getVertex(VectorNf&); void getEdgesWithSamefaceAndGivenOrigins(VertexDCEL<type, dim>* _v1, VertexDCEL<type, dim>* _v2, EdgeDCEL<type, dim>** edge_leaving_v1, EdgeDCEL<type, dim>** edge_leaving_v2); }; 

构造简单多边形的函数

template<typename type, size_t dim> inline PolygonDCEL<type, dim>::PolygonDCEL(std::vector<VetorNf>& _points) { 
    int size = _points.size(); if (size < 3) return; //1.根据所给点，创建vertex for (size_t y = 0; i < _points.size(); ++i) { 
    vertex_list.push_back(new VertexDCEL<type, dim>(_points[i])); } //2.根据创建vertex，创建半边 for (size_t i = 0; i <= vertex_list.size() - 2; ++i) { 
    auto hfedge = new EdgeDCEL<type, dim>(vertex_list[i]); vertex_list[i]->incident_dege = hfedge; auto edge_twin = new EdgeDCEL<type, dim>(vertex_list[i + 1]); hfedge->twin = edge_twin; edge_twin->twin = hfedge; edge_list.push_back(hfedge); edge_list.push_back(edge_twin); } //最后一条边 auto hfedge = new EdgeDCEL<type, dim>(vertex_list.back()); vertex_list[vertex_list.size() - 1]->incident_dege = hfedge; auto edge_twin = new EdgeDCEL<type, dim>(vertex_list.front()); hfedge->twin = edge_twin; edge_twin->twin = hfedge; edge_list.push_back(hfedge); edge_list.push_back(edge_twin); //设置next，prev指针 //edge_list里面是根据半边的顺序存储,所以注意是每隔2个处理一次 for (size_t i = 2; i <= edge_list.size() - 3; ++i) { 
    if (i % 2 == 0)//设置半边 { 
    edge_list[i]->prev = edge_list[i - 2]; edge_list[i]->next = edge_list[i + 2]; } else//设置twin半边 { 
    edge_list[i]->prev = edge_list[i + 2]; edge_list[i]->next = edge_list[i - 2]; } } edge_list[0]->prev = edge_list[edge_list.size() - 2]; edge_list[0]->next = edge_list[2]; edge_list[1]->prev = edge_list[3]; edge_list[1]->next = edge_list[edge_list.size() - 1]; edge_list[edge_list.size() - 2]->prev = edge_list[edge_list.size() - 4]; edge_list[edge_list.size() - 2]->next = edge_list[0]; edge_list[edge_list.size() - 1]->prev = edge_list[1]; edge_list[edge_list.size() - 1]->next = edge_list[edge_list.size() - 3]; //3.新建face FaceDCEL<type, dim>* f1 = new FaceDCEL<type, dim>();//简单多边形的内半边 FaceDCEL<type, dim>* f2 = new FaceDCEL<type, dim>();//简单多边形的外半边 f1->outer = edge_list[0]; f2->inner.push_back(edge_list[1]); //设置整个内部face f1外边界的半边对应incident_face f1->outer->incident_face = f1; EdgeDCEL<type, dim>* edge = f1->outer->next; while (edge!= f1->outer) { 
    edge->incident_face = f1; edge = edge->next; } //设置整个外部face f2内边界的半边对应incident_face f2->inner[0]->incident_face = f2; edge = f2->inner[0]->next; while (edge != f2->inner[0]) { 
    edge->incident_face = f2; edge = edge->next; } } 

重要操作一 找到一个vertex的所有出度边

template<typename type, size_t dim> inline void PolygonDCEL<type, dim>::getEdgesWithSamefaceAndGivenOrigins(VertexDCEL<type, dim>* _v1, VertexDCEL<type, dim>* _v2, EdgeDCEL<type, dim>** edge_leaving_v1, EdgeDCEL<type, dim>** edge_leaving_v2) { 
    std::vector<EdgeDCEL<type, dim>*> edges_with_v1_ori, edges_with_v2_ori; auto v1_inci_edge = _v1->incident_edge; edges_with_v1_ori.push_back(v1_inci_edge); auto next_edge = v1_inci_edge->twin->next; while (next_edge != v1_inci_edge) { 
    edges_with_v1_ori.push_back(next_edge); next_edge = next_edge->twin->next; } auto v2_inci_edge = _v2->incident_edge; edges_with_v2_ori.push_back(v2_inci_edge); auto next_edge = v2_inci_edge->twin->next; while (next_edge != v2_inci_edge) { 
    edges_with_v2_ori.push_back(next_edge); next_edge = next_edge->twin->next; } //edges_with_v1_ori与edges_with_v2_ori里面存的半边对应的incident_face是不一样的 for (auto& ev1 : edges_with_v1_ori) { 
    for (auto& ev2 : edges_with_v2_ori) { 
    if (ev1->incident_face->outer != nullptr) { 
   //找内部的面 if (ev1->incident_face == ev2->incident_face) { 
   //找相同的内部面 //这两条半边必定是相反的方向！！！！可以根据其遍历两个部分 **edge_leaving_v1 = ev1; *edge_leaving_v2 = ev2; return; } } } } } 

重要操作二 split

template<typename type, size_t dim> inline bool PolygonDCEL<type, dim>::split(VertexDCEL<type, dim>* _v1, VertexDCEL<type, dim>* _v2) { 
    EdgeDCEL<type, dim>* edge_oriV1; EdgeDCEL<type, dim>* edge_oriV2; getEdgesWithSamefaceAndGivenOrigins(_v1, _v2, &edge_oriV1, &edge_oriV2); if (edge_oriV1->id == -1 || edge_oriV2->id == -1) return false; //判断是否是邻边 if (edge_oriV1->next->origin == _v2 || edge_oriV1->prev->origin == _v2) return false; //创建新对边 auto half_edge1 = new EdgeDCEL<type, dim>(_v1); auto half_edge2 = new EdgeDCEL<type, dim>(_v2); //设置新半边 half_edge1->twin = half_edge2; half_edge2->twin = half_edge1; half_edge1->next = edge_oriV2; half_edge2->next = edge_oriV1; half_edge1->next->prev = half_edge1; half_edge2->next->prev = half_edge2; half_edge1->prev = edge_oriV1->prev; half_edge2->prev = edge_oriV2->prev; half_edge1->prev->next = half_edge1; half_edge2->prev->next = half_edge2; //新建两个面，并删除旧的面，设置面 FaceDCEL<type, dim>* new_face1 = new FaceDCEL<type, dim>(); new_face1->outer = half_edge1; half_edge1->incident_face = new_face1; auto temp_edge = half_edge1->next; while (temp_edge != half_edge1) { 
    temp_edge->incident_face = new_face1; temp_edge = temp_edge->next; } FaceDCEL<type, dim>* new_face2 = new FaceDCEL<type, dim>(); new_face2->outer = half_edge2; half_edge2->incident_face = new_face2; temp_edge = half_edge2->next; while (temp_edge != half_edge2) { 
    temp_edge->incident_face = new_face2; temp_edge = temp_edge->next; } face_list.push_back(new_face1); face_list.push_back(new_face2); //删除原先的面 FaceDCEL<type, dim>* previous_face = edge_oriV1->incident_face; auto itr = std::find(face_list.begin(), face_list.end(), previous_face); if (itr != face_list.end()) { 
    face_list.erase(itr); delete previous_face; } return true; } 

单调多边形

正例

反例

单调多边形拆分

vertex种类

1.开始顶点
2.结束顶点
3.普通顶点
4.分裂顶点
5.合并顶点

开始顶点与结束顶点是一对，面向多边形内部的角度是锐角

普通顶点，两个端点是上下一侧

分裂顶点和合并顶点是需要实际操作的，单调多边形拆分主要是拆这两个顶点

分裂顶点是与多边形上边内部点相连内对角线，进行拆分。
合并顶点是与多边形下 边内部点相连内对角线，进行拆分。

Plane sweep algorithm

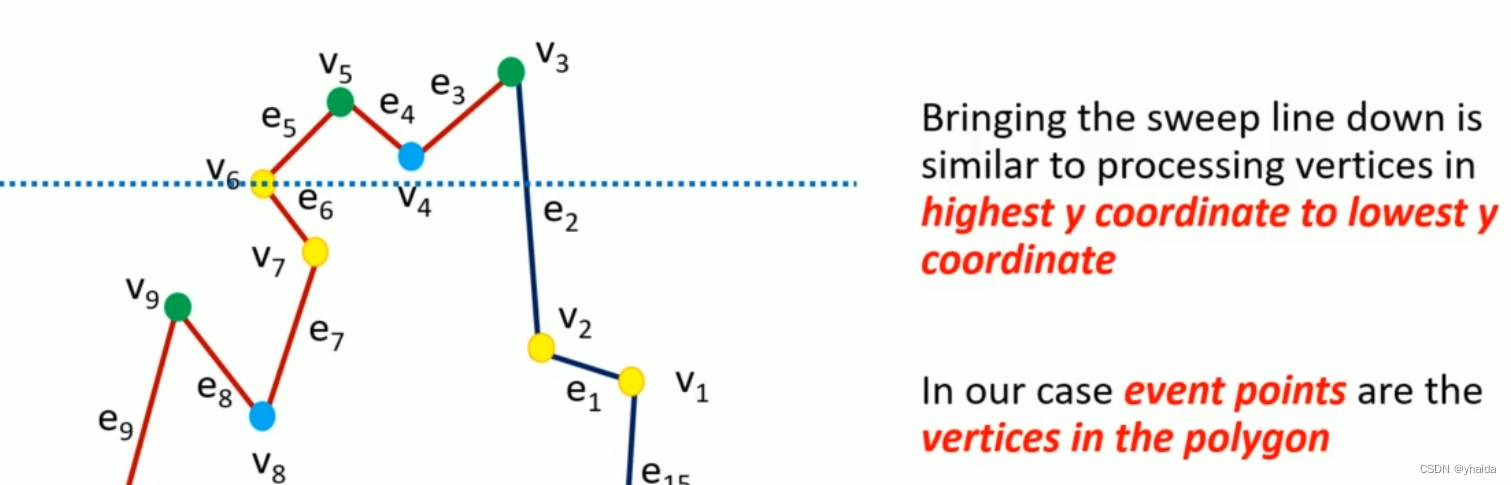
伪代码

辅助顶点

如何去决定内对角线应该和谁相连呢？

对于不同vertex不同的操作

start vertex

end顶点

翻译：
如果边的辅助点的类别在这个顶点结束是一个归并顶点（helper(ei)->merge vertex)，那么我们可以在这个辅助点和当前顶点之间添加一条对角线
从T中删除顶点的端点

分裂顶点

合并顶点

普通顶点