1、时域(时间域)——自变量是时间,即横轴是时间,纵轴是信号的变化。其动态信号x(t)是描述信号在不同时刻取值的函数。
2、频域(频率域)——自变量是频率,即横轴是频率,纵轴是该频率信号的幅度(电压mV,可转为声压dB),也就是通常说的频谱图。
下面是图文讲解:

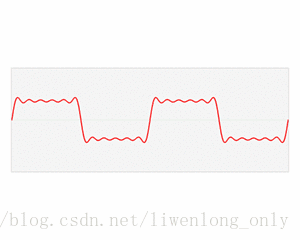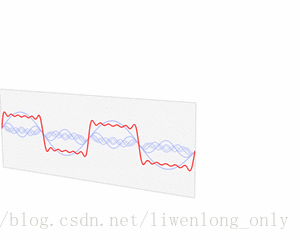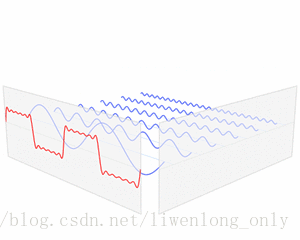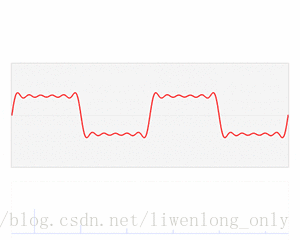
图1是正弦波的时域图,示出了振幅与时间的关系。
在时域图中,横轴是时间,纵轴是振幅。
时域图显示振幅随时间的变化,可以看出峰值振幅为5V,可以算出频率f=6 Hz。

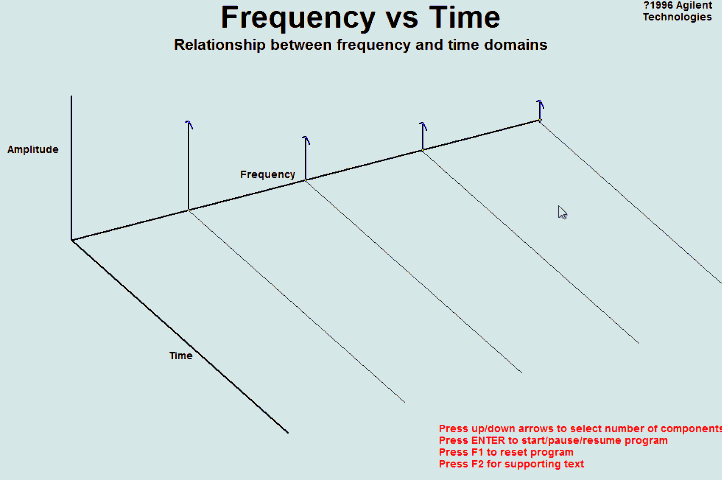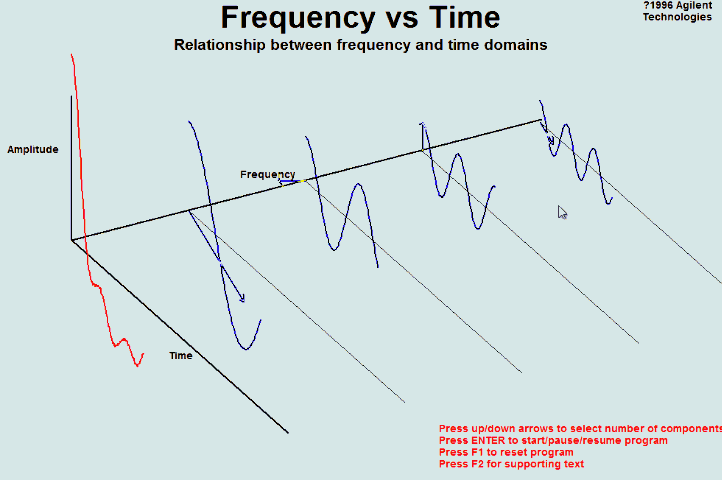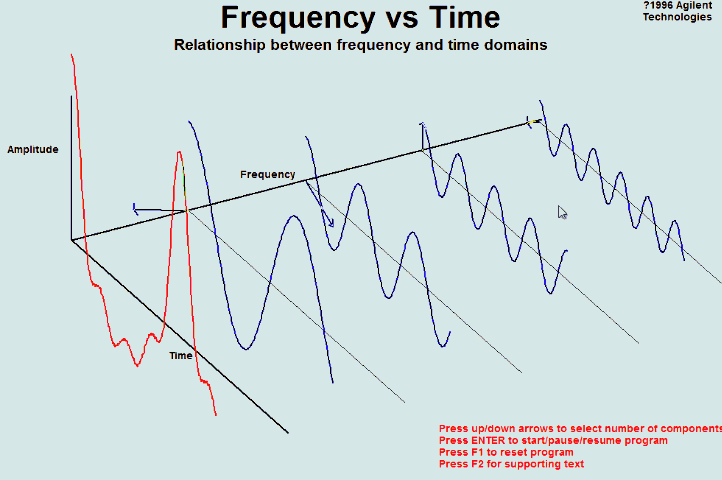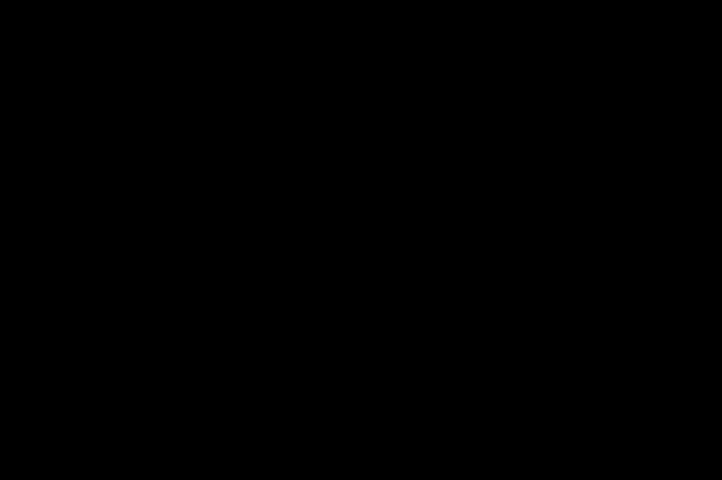
图2是图1中正弦波的频域图
在频域图中,横轴是频率,纵轴是峰值振幅。
频域图仅仅示出峰值振幅与频率,而不显示振幅随时间的变化。
从频域图可以看出,正弦波的频率为6Hz,这个6Hz的正弦波的峰值振幅为5V 。
频域图的优点是,从频域图中,可以一眼看出正弦波的频率和峰值振幅
整个正弦波在频域图上只是一个立柱
立柱的位置显示了正弦波的频率
立柱的高度显示了正弦波的峰值振幅
傅里叶变换(FFT)物理意义:用傅里叶变换将声波变换成频谱和幅度,可以将一个信号变换到频域。有些信号在时域上是很难看出什么特征的,但是如果变换到频域之后,就很容易看出特征了。这就是很多信号分析采用FFT变换的原因。
时域(时间域-time domain)
——自变量是时间,即横轴是时间,纵轴是信号的变化(振幅)。其动态信号x(t)是描述信号在不同时刻取值的函数。
频域(频率域- frequency domain)
——自变量是频率,即横轴是频率,纵轴是该频率信号的幅度(振幅),就是指的信号电压大小,也就是通常说的频谱图。
分析
时域分析函数的参数是时间t,也就是y=f(t),
频域分析时,参数是w,也就是y=F(w)两者之间可以互相转化。时域函数通过傅立叶或者拉普拉斯变换就变成了频域函数。

版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/bian-cheng-ji-chu/82396.html