一、概念总结
在本小节中主要涉及到几个名词,并集、交集、全集和补集,我们通过一个表格来看一下它们的概念
我们这里在描述概念时不在复述课本上的描述,而是用自己的话来描述,更加容易理解
| 名称 | 概念 | 表示符号 |
|---|---|---|
| 并集 | 把两个集合的所有素合并在一起组成的集合叫做两个集合的并集 | ∪ \cup ∪ |
| 交集 | 两个集合的公共素构成的集合叫做两个集合的交集 | ∩ \cap ∩ |
| 全集 | 给定的所有素的集合叫做全集 | U U U |
| 补集 | 全集 U U U中不属于某个集合的全部素构成的集合叫做这个集合的补集 | C u A C_uA CuA |
二、从Venn图理解概念
在第一节的介绍中我们提到了一种集合的表示方法Venn图,它可以让我们直观地看到两个集合之间的关系,下面我们尝试从Venn图的角度来分析一下并集、交集、全集和补集这几个概念。
2.1 全集
我们首先来理解一下全集,给定的所有素可以叫做全集,或者说我们要研究的全部研究对象构成的一个集合也叫做全集,比如我给出一个四边形,它内部的区域就是我们全部的研究对象,那么这个四边形就可以看作一个全集

2.2 并集
假设有两个集合,分别是集合A和集合B,我们把集合A和集合B全部素构成的集合称为并集

图上集合A和集合B的两部分区域加起来就是集合A和集合B的并集,记作 A ∪ B A \cup B A∪B。
我们来举一个更加形象的例子,集合 A = { 1 , 2 , 3 } A = \{1,2,3\} A={ 1,2,3},集合 B = { 4 , 5 , 6 } B = \{4,5,6\} B={ 4,5,6},此时 A ∪ B A \cup B A∪B是什么?很明显,并集是集合A和集合B所有素合在一起构成的集合,所以 A ∪ B = { 1 , 2 , 3 , 4 , 5 , 6 } A \cup B = \{1,2,3,4,5,6\} A∪B={ 1,2,3,4,5,6}。
2.3 交集
还是假设有两个集合,分别是集合A和集合B,两个集合的公共素构成的集合叫做交集,我们可以尝试画一下Venn图
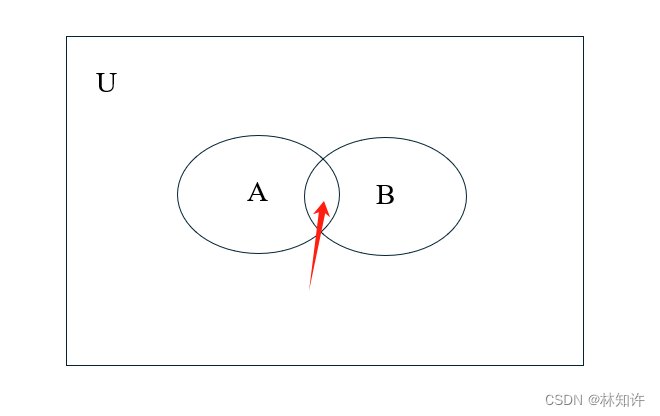
图中A和B相交的部分就是集合A和集合B的交集,记作 A ∩ B A \cap B A∩B。
我们还是来举一个更加形象的例子,集合 A = { 1 , 2 , 3 } A = \{1,2,3\} A={ 1,2,3},集合 B = { 3 , 4 , 5 } B = \{3,4,5\} B={ 3,4,5},此时 A ∩ B A \cap B A∩B是什么?很明显,两个集合的公共素构成的集合叫做交集,所以 A ∩ B = { 3 } A \cap B = \{3\} A∩B={ 3}。
2.4 补集
最后我们来介绍一下补集,全集 U U U中不属于某个集合的全部素构成的集合叫做补集,假设我们有一个集合A,全集U中属于集合A的其余素构成的集合叫做集合A的补集

三、一些结论
下面我们来介绍一些关于并集、交集、全集和补集的结论,可以尝试用Venn图来思考一下为什么
- A ∪ A = A ( A 并 A 等于 A ) A \cup A = A(A并A等于A) A∪A=A(A并A等于A)
- A ∪ ∅ = A ( A 并空集等于 A ) A \cup \emptyset = A(A并空集等于A) A∪∅=A(A并空集等于A)
- A ∩ A = A ( A 交 A 等于 A ) A \cap A = A(A交A等于A) A∩A=A(A交A等于A)
- A ∩ ∅ = ∅ ( A 交空集等于空集) A \cap \emptyset = \emptyset(A交空集等于空集) A∩∅=∅(A交空集等于空集)
- A ∪ B = B ∪ A ( A 并 B 等于 B 并 A ) A \cup B = B \cup A(A并B等于B并A) A∪B=B∪A(A并B等于B并A)
- A ∩ B = B ∩ A ( A 交 B 等于 B 交 A ) A \cap B = B \cap A(A交B等于B交A) A∩B=B∩A(A交B等于B交A)
- A ∪ B ⊇ A ( A 并 B 包含 A ) A \cup B \supseteq A(A并B包含A) A∪B⊇A(A并B包含A)
- A ∪ B ⊇ B ( A 并 B 包含 B ) A \cup B \supseteq B(A并B包含B) A∪B⊇B(A并B包含B)
- A ∩ B = A ⇔ A ⊆ B ( A 交 B 等于 A 等价于 A 包含于 B ) A \cap B = A \Leftrightarrow A \subseteq B(A交B等于A等价于A包含于B) A∩B=A⇔A⊆B(A交B等于A等价于A包含于B)
- A ∪ B = A ⇔ A ⊇ B ( A 并 B 等于 A 等价于 A 包含 B ) A \cup B = A \Leftrightarrow A \supseteq B(A并B等于A等价于A包含B) A∪B=A⇔A⊇B(A并B等于A等价于A包含B)
- A ∪ C u A = U ( A 并 A 的补集等于全集) A \cup C_uA = U(A并A的补集等于全集) A∪CuA=U(A并A的补集等于全集)
- A ∩ C u A = ∅ ( A 交 A 的补集等于空集) A \cap C_uA = \emptyset(A交A的补集等于空集) A∩CuA=∅(A交A的补集等于空集)
- C u ( C u A ) = A ( A 的补集的补集等于 A ) C_u(C_uA) = A(A的补集的补集等于A) Cu(CuA)=A(A的补集的补集等于A)
虽然上面这些结论看起来很多,但是呢它确实很多(开个玩笑),虽然他们确实很多,但是万变不离其宗,只要我们清晰地理解的并集、交集、全集和补集的概念,能够学会使用Venn图来分析,那么以后遇到其他类似的结论,判断起来也不成问题。
今天的文章 【数学(一)集合与常用逻辑用语】集合的基本运算分享到此就结束了,感谢您的阅读。

版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/bian-cheng-ji-chu/82787.html