0:关于基本数学应用的问题:
1:正弦余弦曲线:更一般应用的正弦曲线公式为:
A 为波幅(纵轴), ω为(相位矢量)角频率=2PI/T,T为周期, t 为时间(横轴), θ 为相位(横轴左右)。
![[转载]曲线拟合鈥斺1、了解基本初等函数图形 [转载]曲线拟合鈥斺1、了解基本初等函数图形](/uploads/202410/10/20074b3421525411.webp)
周期函数:正余弦函数可用来表达周期函数。
余弦函数的(通常是无限的)和;这是傅立叶分析的基础想法。例如,方波可以写为傅立叶级数:
在动画中,可以看到只用少数的项就已经形成了非常准确的估计。
如果明白了上书基本原理,也就不难理解我所用的浮动频率合成曲线的道理。
2:指数函数:形如y=kax 的函数,k为常系数,这里的 a 叫做“底数”,是不等于 1的任何正实数。指数函数按恒定速率翻倍,可以用来表达形象与刻画发展型的体系,比如金价2001年以来的牛市轨迹基本就是指数方程曲线。
![[转载]曲线拟合鈥斺1、了解基本初等函数图形 [转载]曲线拟合鈥斺1、了解基本初等函数图形](/uploads/202410/10/20074b3421525411.webp)
特例:应用到值 x 上的这个函数可写为exp(x)。还可以等价的写为 ex,这里的e 是数学常数,就是自然对数的底数,近似等于 2.,还叫做欧拉数。
即函数:
定义于所有的 a >0,和所有的实数 x。它叫做底数为 a 的指数函数。注意这个 的定义依赖于先前确立的定义于所有实数上的函数
的定义依赖于先前确立的定义于所有实数上的函数 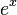 的存在。注意上述等式对于 a = e 成立,因为
的存在。注意上述等式对于 a = e 成立,因为
指数函数可“在加法和乘法之间转换”,在下列“指数定律”的前三个和第五个中表述:
它们对所有正实数 a 与 b 和所有实数x 与 y 都是有效的。
![[转载]曲线拟合鈥斺1、了解基本初等函数图形 [转载]曲线拟合鈥斺1、了解基本初等函数图形](/uploads/202410/10/20074b3421525411.webp)
3:幂函数:是形如f(x)=xa的函数,a可以是自然数,有理数,也可以是任意实数或复数。
下图是幂函数; 自上至下: x1/8, x1/4,x1/2, x1, x2,x4, x8
语言学中Zipf定律与经济学中的Pareto定律都是简单的幂函数,也称之为幂律分布;还有其它形式的幂律分布,像名次——规模分布、规模——概率分布,这四种形式在数学上是等价的,幂律分布的示意图如图1右图所示,其通式可写成y=c*x^(-r),其中x,y是正的随机变量,c,r均为大于零的常数。这种分布的共性是绝大多数事件的规模很小,而只有少数事件的规模相当大。对上式两边取对数,可知lny与lnx满足线性关系,也即在双对数坐标下,幂律分布表现为一条斜率为幂指数的负数的直线,这一线性关系是判断给定的实例中随机变量是否满足幂律的依据。
幂率的另一层重要意义:理解幂律分布就是所谓的马太效应,二八原则,即少数人聚集了大量的财富,而大多数人的财富数量都很小。
4:对数函数曲线:群论对于对数的视角,是俺常用的:即从纯数学的观点来看,恒等式
-
 ,
,
在两种意义上是基本的。首先,其他算术性质可以从它得出。进一步的,它表达了在正实数的乘法群和所有实数的加法群之间的同构。对数函数是从正实数的乘法群到实数的加法群的唯一连续同构。
![[转载]曲线拟合鈥斺1、了解基本初等函数图形 [转载]曲线拟合鈥斺1、了解基本初等函数图形](/uploads/202410/10/20074b3421525411.webp)
5:均匀分布:
先看一下离散型均匀分布,在概率论中,离散型均匀分布是一个离散型概率,其中有限个数值拥有相同的概率。设随机变量X取n个不同的值,其概率分布为:
P{X=xi}=1/n,i=1,2...n;
这个东西表面看起来抽象,其实只需要记住一个例子就很好理解,赌博用的有6个面的骰子,6个面出现的几率是相等的,即为均匀分布。
连续型均匀分布,如果连续型随机变量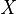 具有如下的概率密度函数,则称
具有如下的概率密度函数,则称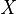 服从
服从![一些常用函数的曲线图及应用简说 [a,b]](http://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) 上的均匀分布(uniformdistribution),记作
上的均匀分布(uniformdistribution),记作![一些常用函数的曲线图及应用简说 X \sim U[a,b]](http://upload.wikimedia.org/math/1/2/c/12cc87a67ce350e5ec7bef503d6b7950.png)
概率密度函数:
期望值(即均值):
均匀分布具有下属意义的等可能性。若![一些常用函数的曲线图及应用简说 X \sim U[a,b]](http://upload.wikimedia.org/math/1/2/c/12cc87a67ce350e5ec7bef503d6b7950.png) ,则X落在[a,b]内任一子区间[c,d]上的概率:
,则X落在[a,b]内任一子区间[c,d]上的概率:
只与区间[c,d]的长度有关,而与他的位置无关。
均匀分布可以代表信息极度贫乏的体系或无序状态的体系。而如果一个系统不属于均匀分布或随机游走,即均匀分布或随机游走的否定,就等于肯定了该系统具有信息,或者说具有某种程度的有序性。这个就是均匀分布的实际应用价值之一。
今天的文章 一些常用函数的曲线图及应用简说分享到此就结束了,感谢您的阅读。


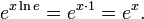
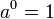
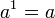
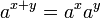
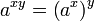

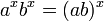
 ,
,

![一些常用函数的曲线图及应用简说 E[X]=\frac{a+b}{2}](http://upload.wikimedia.org/math/5/e/9/5e9fe55d33810582232765e5778120de.png)
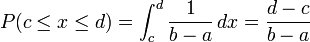
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/bian-cheng-ji-chu/84351.html