知识点
光子不仅有能量 E = h ν E=h\nu E=hν,还有动量 p = h λ = ℏ k p=\frac{h}{\lambda}=\hbar k p=λh=ℏk, k k k为波矢, k = 2 π / λ k=2\pi/\lambda k=2π/λ。
普朗克常量作为普适常量将标志波动性质的 ν \nu ν和 λ ( k ) \lambda(k) λ(k),同标志粒子性质的 E E E和 p p p联系起来了。
德布罗意关系式: λ = h p \lambda=\frac{h}{p} λ=ph。在非相对论近似下: λ = h p = h 2 m E k = h c 2 m E k c 2 \lambda=\frac{h}{p}=\frac{h}{\sqrt{2mE_k}}=\frac{hc}{\sqrt{2mE_kc^2}} λ=ph=2mEkh=2mEkc2hc,则电子的德布罗意波长 λ = 1.226 E k ( e V ) n m \lambda=\frac{1.226}{\sqrt{E_k(eV)}}nm λ=Ek(eV)1.226nm。
爱因斯坦质能方程, E 2 = p 2 c 2 + m 0 2 c 4 E^2=p^2c^2+m_0^2c^4 E2=p2c2+m02c4 ( 1 ) ^{(1)} (1), E = m c 2 = m 0 c 2 + E k E=mc^2=m_0c^2+E_k E=mc2=m0c2+Ek, m 0 m_0 m0为静止质量,相对论质量 m = m 0 1 − v 2 / c 2 m=\frac{m_0}{\sqrt{1-v^2/c^2}} m=1−v2/c2m0。
光子的静止质量为 0 0 0,光子动能: E = p c = h c λ = 1.24 n m ⋅ k e V 0.4 n m = 3.1 × 1 0 3 e V E=pc=\frac{hc}{\lambda}=\frac{1.24\mathrm{nm\cdot keV}}{0.4\mathrm{nm}}=3.1\times 10^3 eV E=pc=λhc=0.4nm1.24nm⋅keV=3.1×103eV。
E = m c 2 ≈ m 0 c 2 ( 1 + v 2 c 2 ) E=mc^2\approx m_0c^2(1+\frac{v^2}{c^2}) E=mc2≈m0c2(1+c2v2) ( 2 ) ^{(2)} (2),由 ( 1 ) − ( 2 ) 2 (1)-(2)^2 (1)−(2)2,即得: p 2 c 2 = 2 E k E 0 + E k 2 = 2 m 0 c 2 E k + E k 2 p^2c^2=2E_kE_0+E_k^2=2m_0c^2E_k+E_k^2 p2c2=2EkE0+Ek2=2m0c2Ek+Ek2,(2)式中将 E k E_k Ek近似为 m 0 v 2 m_0v^2 m0v2。
已知波长时,中子能量的计算 E = p 2 2 m n = h 2 2 m n λ 2 = ( h c ) 2 2 m n c 2 λ 2 = ( 1.24 n m ⋅ k e V ) 2 2 × 940 M e V × λ 2 E=\frac{p^2}{2m_n}=\frac{h^2}{2m_n\lambda^2}=\frac{(hc)^2}{2m_nc^2\lambda^2}=\frac{(1.24 \mathrm{nm\cdot keV})^2}{2\times 940\mathrm{MeV}\times \lambda^2} E=2mnp2=2mnλ2h2=2mnc2λ2(hc)2=2×940MeV×λ2(1.24nm⋅keV)2。通过分子分母同乘 c c c以达到凑常数的目的。
德布罗意波的实验验证:汤姆逊电子衍射实验。
戴维逊-革末实验
反射表面可看成光栅,
晶体中发生衍射的条件: d sin θ = n λ d\sin{\theta}=n\lambda dsinθ=nλ,出现反射波加强的条件: 2 d sin θ = n λ 2d\sin{\theta}=n\lambda 2dsinθ=nλ。
海森堡不确定关系,又称测不准关系,它包括多种关系式,其中两种是 Δ x Δ p x ≥ ℏ 2 \Delta x\Delta p_x\geq \frac{\hbar}{2} ΔxΔpx≥2ℏ, Δ E Δ t ≥ ℏ 2 \Delta E\Delta t\geq \frac{\hbar}{2} ΔEΔt≥2ℏ,其揭示了一条重要的物理规律,粒子在客观上不能同时具有坐标位置和相应的动量。而所谓的不确定或测不准只是粒子的客观属性,不能同时具有坐标位置和相应的动量,因此,我们不赞成将其称为测不准关系。
Δ E \Delta E ΔE指粒子在某一状态能量的不确定度, Δ t \Delta t Δt为粒子处于某一状态的时间,即该状态的寿命, Δ E Δ t ≥ ℏ 2 \Delta E\Delta t\geq \frac{\hbar}{2} ΔEΔt≥2ℏ说明粒子在某一状态的能量与粒子在该状态的寿命是无法同时确定的。
已知波长的不确定度求能量不确定度: Δ E = h Δ ν = h c λ Δ λ λ \Delta E=h\Delta \nu=\frac{hc}{\lambda}\frac{\Delta \lambda}{\lambda} ΔE=hΔν=λhcλΔλ。
我们在第二章中给出了电子的玻尔第一半径 r 1 = 0.053 n m r_1=0.053\mathrm{nm} r1=0.053nm与相应的动量 p 1 = m v 1 = m c α p_1=mv_1=mc\alpha p1=mv1=mcα,从不确定性关系看,电子的位置如果确定在 r 1 r_1 r1轨道上,那它的动量就完全不确定,我们假设电子在 r 1 r_1 r1内运动, Δ x = r 1 \Delta x=r_1 Δx=r1,则相应的 Δ p / p \Delta p/p Δp/p为
Δ p p = ℏ / 2 Δ x p = ℏ c 2 m c 2 α Δ x = 0.197 n m ⋅ k e V 2 × 511 k e V ( 137 ) − 1 0.053 n m = 0.50 \frac{\Delta p}{p}=\frac{\hbar/2\Delta x}{p}=\frac{\hbar c}{2mc^2\alpha\Delta x}=\frac{0.197\mathrm{nm\cdot keV}}{2\times 511\mathrm{keV}\ (137)^{-1}0.053\mathrm{nm}}=0.50 pΔp=pℏ/2Δx=2mc2αΔxℏc=2×511keV (137)−10.053nm0.197nm⋅keV=0.50
由计算结果可知,我们无法确切的说明在 r 1 r_1 r1范围内运动的电子具有多大动量。
对于原子尺寸的粒子,我们不能用经典的方法来描述,轨道的概念是没有意义的,因为它是建立在有同时确定的位置和动量的基础上的。
对玻尔模型中跃迁的解释;跃迁是没有中间停留态过程的,即能量经历的状态是能量完全不确定的状态, 即 Δ E = ∞ \Delta E=\infty ΔE=∞,故 Δ t = 0 \Delta t=0 Δt=0,跃迁不需要时间。
同时,原子激发态能级总是有一定分布宽度 Δ E n \Delta E_n ΔEn,所以辐射跃迁发出的光波不可能是严格的单色波。处于任一激发态的原子,它不可能永远处于该能级,即该能级的寿命总是有限的,其 Δ E ≠ 0 \Delta E\neq0 ΔE=0故 Δ t ≠ ∞ \Delta t\neq \infty Δt=∞。
由于自由粒子的波长不变,它可以用一个平面单色波来表示,即 ψ ( r ⃗ , t ) = ψ 0 cos ( k ⃗ ⋅ r ⃗ − ω t ) \psi(\vec{r},t)=\psi_0 \cos({\vec{k}\cdot \vec{r} - \omega t}) ψ(r,t)=ψ0cos(k⋅r−ωt),其中 k ⃗ = 2 π P ⃗ h = p ℏ \vec{k}=\frac{2\pi \vec{P}}{h}=\frac{p}{\hbar} k=h2πP=ℏp,用复数表示为 ψ ( r ⃗ , t ) = ψ 0 e i ( k ⃗ ⋅ r ⃗ − ω t ) = ψ 0 e i ℏ ( P ⃗ ⋅ r ⃗ − E t ) \psi(\vec{r},t)=\psi_0 e^{i(\vec{k}\cdot \vec{r} - \omega t)}=\psi_0 e^{\frac{i}{\hbar}(\vec{P}\cdot \vec{r} - E t)} ψ(r,t)=ψ0ei(k⋅r−ωt)=ψ0eℏi(P⋅r−Et),其中 P ⃗ = ℏ k ⃗ , E = ℏ ω \vec{P}=\hbar \vec{k}, E=\hbar \omega P=ℏk,E=ℏω。它表示一个振幅恒定,在时间和空间上无限延展的波。
振幅就是几率波幅,这就是波动性的物理含义。而经典意义下的描述波动的函数或复振幅就成了量子意义下描述粒子分布几率的函数–波函数。几率波把物质粒子的波动性与粒子性正确的统一起来了。
ψ 1 , ψ 2 \psi_{1}, \psi_{2} ψ1,ψ2 光子本征态; ψ = ψ 1 + ψ 2 \psi=\psi_{1}+\psi_{2} ψ=ψ1+ψ2态叠加原理;
I = ∣ ψ ∣ 2 = ( ψ 1 ∗ + ψ 2 ∗ ) ( ψ 1 + ψ 2 ) = ∣ ψ 1 ∣ 2 + ∣ ψ 2 ∣ 2 + ψ 1 ∗ ψ 2 + ψ 2 ∗ ψ 1 I =|\psi|^{2}=\left(\psi_{1}^{*}+\psi_{2}^{*}\right)\left(\psi_{1}+\psi_{2}\right) =\left|\psi_{1}\right|^{2}+\left|\psi_{2}\right|^{2}+\psi_{1}^{*} \psi_{2}+\psi_{2}^{*} \psi_{1} I=∣ψ∣2=(ψ1∗+ψ2∗)(ψ1+ψ2)=∣ψ1∣2+∣ψ2∣2+ψ1∗ψ2+ψ2∗ψ1,后两项为干涉项。
干涉实际上是一个光子的两个本征态之间的干涉。
粒子不能产生和湮灭,即总能在空间某处发现该粒子,必须有, ∫ V ∣ ψ ( x , t ) ∣ 2 d X = 1 \int_{V}|\psi(x, t)|^{2} d X=1 ∫V∣ψ(x,t)∣2dX=1,由于几率是相对的,积分也可能等于常数 ∫ V ∣ ψ ( x , t ) ∣ 2 d X = A \int_{V}|\psi(x, t)|^{2} d X=A ∫V∣ψ(x,t)∣2dX=A。对于不等于 1 1 1的积分可以进行归一化, ∫ V ∣ ψ ( x , t ) A ∣ 2 d X = 1 \int_{V}|\frac{\psi(x, t)}{\sqrt{A}}|^{2} d X=1 ∫V∣Aψ(x,t)∣2dX=1。
事实上,归一化并非总是需要的,而且有些波函数不能归一化,例如单色波或自由粒子,由于它们在空间各处的几率都相等,因而有: ∫ V ∣ ψ ( x , t ) ∣ 2 d X = ∫ − ∞ + ∞ ∣ ψ 0 e i ( K ⃗ ⋅ r ⃗ − ω t ) ∣ 2 d X = ψ 0 2 ∫ − ∞ + ∞ d X = ∞ \int_{V}|\psi(x, t)|^{2} d X =\int_{-\infty}^{+\infty}\left|\psi_{0} e^{i(\vec{K} \cdot \vec{r}-\omega t)}\right|^{2} d X =\psi_{0}^{2} \int_{-\infty}^{+\infty} d X=\infty ∫V∣ψ(x,t)∣2dX=∫−∞+∞∣∣∣ψ0ei(K⋅r−ωt)∣∣∣2dX=ψ02∫−∞+∞dX=∞
粒子的 x x x坐标在 0 0 0到 a a a之间的概率: P = ∫ 0 a d x ∫ − ∞ ∞ d y ∫ − ∞ ∞ d z ( ψ ∗ ψ ) P=\int_0^a dx \int_{-\infty}^\infty dy\int_{-\infty}^\infty dz(\psi^*\psi) P=∫0adx∫−∞∞dy∫−∞∞dz(ψ∗ψ)
位矢 x ⃗ = ( x e x , y e y , z e z ) \vec{x}=\left(x \boldsymbol{e}_{x}, y \boldsymbol{e}_{y}, z \boldsymbol{e}_{z}\right) x=(xex,yey,zez),波矢 k ⃗ = ( k x e x , k y e y , k z e z ) \vec{k}=\left(k_{x} \boldsymbol{e}_{x}, k_{y} \boldsymbol{e}_{y}, k_{z} \boldsymbol{e}_{z}\right) k=(kxex,kyey,kzez),粒子的动量 p ⃗ = ( p x e x , p y e y , p z e z ) \vec{p}=\left(p_{x} \boldsymbol{e}_{x}, p_{y} \boldsymbol{e}_{y}, p_{z} \boldsymbol{e}_{z}\right) p=(pxex,pyey,pzez)
- 自由粒子的薛定谔方程 (或者单色平面波的薛定谔方程)
波函数 ψ ( x , t ) = ψ 0 e i ( k ⋅ x − ω t ) = ψ 0 e i ( p ⋅ x − E t ) / ℏ \psi(\boldsymbol{x}, t)=\psi_{0} \mathrm{e}^{i(k \cdot x-\omega t)}=\psi_{0} \mathrm{e}^{i(p \cdot x-E t) / \hbar} ψ(x,t)=ψ0ei(k⋅x−ωt)=ψ0ei(p⋅x−Et)/ℏ
将波函数对时间微分得, i ℏ ∂ ( x , t ) ∂ t = ℏ ω ψ ( x , t ) = E ψ ( x , t ) i\hbar\frac{\partial (x,t)}{\partial t}=\hbar \omega\psi(x,t)=E\psi(x,t) iℏ∂t∂(x,t)=ℏωψ(x,t)=Eψ(x,t),再对坐标变量微分两次,则得 − ℏ 2 ∂ 2 ψ ( x , t ) ∂ x 2 = p x 2 ψ ( x , t ) -\hbar^{2} \frac{\partial^{2} \psi(\boldsymbol{x}, t)}{\partial x^{2}}=p_{x}^{2} \psi(\boldsymbol{x}, t) −ℏ2∂x2∂2ψ(x,t)=px2ψ(x,t),在三维空间中 − ℏ 2 2 m ∇ 2 ψ ( x , t ) = p 2 2 m ψ ( x , t ) = E k ψ ( x , t ) -\frac{\hbar^{2}}{2 m} \nabla^{2} \psi(\boldsymbol{x}, t)=\frac{p^{2}}{2 m} \psi(\boldsymbol{x}, t)=E_{k} \psi(\boldsymbol{x}, t) −2mℏ2∇2ψ(x,t)=2mp2ψ(x,t)=Ekψ(x,t)。由于自由粒子不受外力,没有势能,它的总能量就是它的动能,故 E = E k = p 2 2 m E=E_{k}=\frac{p^{2}}{2 m} E=Ek=2mp2,所以 i ℏ ∂ ψ ( x , t ) ∂ t = E ψ ( x , t ) = E k ψ ( x , t ) i \hbar \frac{\partial \psi(\boldsymbol{x}, t)}{\partial t}=E \psi(\boldsymbol{x}, t)=E_{k} \psi(\boldsymbol{x}, t) iℏ∂t∂ψ(x,t)=Eψ(x,t)=Ekψ(x,t),
因此自由粒子的薛定谔方程: i ℏ ∂ ψ ( x , t ) ∂ t = − ℏ 2 2 m ∇ 2 ψ ( x , t ) i \hbar \frac{\partial \psi(\boldsymbol{x}, t)}{\partial t}=-\frac{\hbar^{2}}{2 m} \nabla^{2} \psi(\boldsymbol{x}, t) iℏ∂t∂ψ(x,t)=−2mℏ2∇2ψ(x,t)
- 势场(外场)中粒子的薛定谔方程
对于处于势场中的粒子,除了动能,还有势能。哈密顿量: E = E k + E p = p 2 2 m + V ( r , t ) E=E_k+E_p=\frac{p^2}{2m}+V(\boldsymbol{r},t) E=Ek+Ep=2mp2+V(r,t),哈密顿算符 − ℏ 2 2 m ∇ 2 + V ( r , t ) -\frac{\hbar^2}{2m}\nabla^2+V(\boldsymbol{r},t) −2mℏ2∇2+V(r,t)。
势场中运动粒子的薛定谔方程: i ℏ ∂ ψ ( r , t ) ∂ t = [ − ℏ 2 2 m ∇ 2 + V ( r ) ] ψ ( r , t ) i \hbar \frac{\partial \psi(\boldsymbol{r}, t)}{\partial t}=[-\frac{\hbar^2}{2m}\nabla^2+V(\boldsymbol{r})] \psi(\boldsymbol{r}, t) iℏ∂t∂ψ(r,t)=[−2mℏ2∇2+V(r)]ψ(r,t)
与经典粒子能量表达式 E = p 2 2 m + V ( r , t ) E=\frac{p^2}{2m}+V(\boldsymbol{r},t) E=2mp2+V(r,t) 对应,可以看做是如下变换 E → i ℏ ∂ ∂ t , p ⃗ = − i ℏ ∇ , E k → − ℏ 2 2 m ∇ 2 E\rightarrow i\hbar \frac{\partial}{\partial t},\quad \vec{p}=-i\hbar \nabla,\quad E_k\rightarrow -\frac{\hbar^2}{2m}\nabla^2 E→iℏ∂t∂,p=−iℏ∇,Ek→−2mℏ2∇2 作用到波函数上的结果。
- 定态薛定谔方程
如果势能函数不含时间,则对于定态势能场,有 V ( r , t ) = V ( r ) V(\boldsymbol{r},t)=V(\boldsymbol{r}) V(r,t)=V(r),可以利用分离变量法 ψ ( r , t ) = ψ ( r ) f ( t ) \psi(r,t)=\psi(r)f(t) ψ(r,t)=ψ(r)f(t)化简。
[ − ℏ 2 2 m ∇ 2 + V ( r ) ] ψ ( r ) = E ψ ( r ) [-\frac{\hbar^2}{2m}\nabla^2+V(\boldsymbol{r})] \psi(\boldsymbol{r})=E\psi(r) [−2mℏ2∇2+V(r)]ψ(r)=Eψ(r),方程的解为: ψ ( r , t ) = ψ ( r ) e − i E t / h \psi(r,t)=\psi(r)e^{-iEt/h} ψ(r,t)=ψ(r)e−iEt/h
发生从 i i i态到 f f f态跃迁的概率 ω i → f \omega_{i\rightarrow f} ωi→f或 ω i f \omega_{if} ωif,可表示为 w i f = ∣ ⟨ f ∣ i ⟩ ∣ 2 w_{i f}=|\langle f \mid i\rangle|^{2} wif=∣⟨f∣i⟩∣2, ⟨ f ∣ i ⟩ \langle f \mid i\rangle ⟨f∣i⟩即表示从 i i i态到 f f f态跃迁的概率幅,或概率振幅,相当于 ψ \psi ψ。
算符&力学量的平均值
如果 Ψ ( x ) \Psi(x) Ψ(x) 为粒子的波函数, ∣ Ψ ( x ) ∣ 2 |\Psi(x)|^{2} ∣Ψ(x)∣2 表示粒子在 x x x 处出现的几率,即粒子的位置值等于 x x x 的几率. 则 x x x 的平均值(一维)为:
x ˉ = ∫ x ∣ ψ ( x ) ∣ 2 d x = ∫ ψ ∗ ( x ) x ψ ( x ) d x = ∫ ψ ∗ ( x ) [ x ^ ψ ( x ) ] d x \bar{x}=\int x|\psi(x)|^{2} \mathrm{~d} x=\int \psi^{*}(x) x \psi(x) \mathrm{d} x =\int \psi^{*}(x)[\hat{x} \psi(x)] \mathrm{d} x xˉ=∫x∣ψ(x)∣2 dx=∫ψ∗(x)xψ(x)dx=∫ψ∗(x)[x^ψ(x)]dx
势能的平均值
粒子的势能由其位置决定,可以仿照平均值位置的方法,其势能等于 V ( x ) V(x) V(x) 的几率,就是粒子在 x x x 出现的几率为 ∣ Ψ ( x ) ∣ 2 |\Psi(x)|^{2} ∣Ψ(x)∣2 ,则 V ( x ) V(x) V(x) 的平均值为:
V ˉ = ∫ V ( x ) ∣ ψ ( x ) ∣ 2 d x = ∫ ψ ∗ ( x ) [ V ψ ( x ) ] d x = ∫ ψ ∗ ( x ) [ V ^ ψ ( x ) ] d x \bar{V}=\int V(x)|\psi(x)|^{2} \mathrm{~d} x=\int \psi^{*}(x)[V \psi(x)] \mathrm{d} x=\int \psi^{*}(x)[\hat{V} \psi(x)] \mathrm{d} x Vˉ=∫V(x)∣ψ(x)∣2 dx=∫ψ∗(x)[Vψ(x)]dx=∫ψ∗(x)[V^ψ(x)]dx
动量的平均值
不确定关系表明,动量和位置不可能同时有确定的值,粒子的动量在 ( p , p + d p ) (p, p+d p) (p,p+dp) 的几率,不能直接用 Ψ ( x ) \Psi(x) Ψ(x) 描述, p ‾ = ∫ x ψ ∗ p ^ ψ d x \overline{p}=\int_x \psi^{*} \hat{\boldsymbol{p}} \psi \mathrm{d} \boldsymbol{x} p=∫xψ∗p^ψdx,动量算符: p ^ = − i ℏ ∇ \hat{p}=-i \hbar \nabla p^=−iℏ∇,动量 x x x 分量算符: p ^ x = − i ℏ ∂ ∂ x \quad \hat{p}_{x}=-i \hbar \frac{\partial}{\partial x} p^x=−iℏ∂x∂
动能 T = p 2 / 2 m T=p^2/2m T=p2/2m 的平均值: T ‾ = ∫ x ψ ∗ ( − ℏ 2 2 m ∇ 2 ) ψ d x \overline{T}=\int_x \psi^{*} (-\frac{\hbar^2}{2m}\nabla^2) \psi \mathrm{d} \boldsymbol{x} T=∫xψ∗(−2mℏ2∇2)ψdx
粒子总能量 E = p 2 / 2 m + V E=p^2/2m+V E=p2/2m+V 的平均值: E ‾ = ∫ − ∞ ∞ ψ ∗ ( − ℏ 2 2 m ∇ 2 + V ) ψ d x = ∫ − ∞ ∞ ψ ∗ H ^ ψ d x \overline{E}=\int_{-\infty}^{\infty} \psi^{*} (-\frac{\hbar^2}{2m}\nabla^2+V) \psi \mathrm{d} \boldsymbol{x}=\int_{-\infty}^{\infty} \psi^{*}\hat{H} \psi \mathrm{d} \boldsymbol{x} E=∫−∞∞ψ∗(−2mℏ2∇2+V)ψdx=∫−∞∞ψ∗H^ψdx
通常情况下,粒子的任何一个力学量 A A A的平均值可以直接写为: A ‾ = ∫ ψ ∗ ( r ) A ^ ψ ( r ) d τ = ∫ ψ ∗ ( x ) A ^ ψ ( x ) d 3 x \overline{A}=\int \psi^*(r)\hat{A}\psi(r)d\tau=\int \psi^*(x)\hat{A}\psi(x)d^3x A=∫ψ∗(r)A^ψ(r)dτ=∫ψ∗(x)A^ψ(x)d3x,当 ψ \psi ψ的参数都为实数时, A ‾ = ∫ ∣ ψ ∣ 2 A ^ d τ = ∫ ∣ ψ ∣ 2 A ^ r π r 2 d r \overline{A}=\int \mid{\psi}\mid^2\hat{A}d\tau=\int \mid{\psi}\mid^2\hat{A}r\pi r^2 dr A=∫∣ψ∣2A^dτ=∫∣ψ∣2A^rπr2dr
一维无限深势阱
利用分离变量法解定态薛定谔方程: ℏ 2 2 m ψ ( x ) + E ψ ( x ) = 0 \frac{\hbar^2}{2m} \psi(\boldsymbol{x})+E\psi(x)=0 2mℏ2ψ(x)+Eψ(x)=0即可,代入边界条件即可解得:
一维无限深阱中运动的粒子的本征态为
ψ n ( x ) = { 2 a sin ( n π x a ) ( n = 1 , 2 , 3 , ⋯ ; 0 ⩽ x ⩽ a ) 0 ( x < 0 , x > a ) \psi_{n}(x)= \begin{cases}\sqrt{\frac{2}{a}} \sin \left(\frac{n \pi x}{a}\right) & (n=1,2,3, \cdots ; 0 \leqslant x \leqslant a) \\ 0 & (x<0, x>a)\end{cases} ψn(x)={
a2sin(anπx)0(n=1,2,3,⋯;0⩽x⩽a)(x<0,x>a)
E n = n 2 h 2 8 m d 2 E_n=\frac{n^2h^2}{8md^2} En=8md2n2h2
一维有限深势阱
在阱内 ( ∣ x ∣ < d 2 ) \left(|x|<\frac{d}{2}\right) (∣x∣<2d) 的情况已由上一小节给出,波函数为正弦函数;
在阱外 ( ∣ x ∣ ⩾ d 2 ) \left(|x| \geqslant \frac{d}{2}\right) (∣x∣⩾2d), 体系所满足的薛定谔方程是
d 2 ψ d x 2 = 2 m ( V d − E ) ℏ 2 ψ ≡ k d 2 ψ k d 2 ≡ 2 m ( V d − E ) ℏ 2 \begin{gathered} \frac{\mathrm{d}^{2} \psi}{\mathrm{d} x^{2}}=\frac{2 m\left(V_{d}-E\right)}{\hbar^{2}} \psi \equiv k_{d}^{2} \psi \\ k_{d}^{2} \equiv \frac{2 m\left(V_{d}-E\right)}{\hbar^{2}} \end{gathered} dx2d2ψ=ℏ22m(Vd−E)ψ≡kd2ψkd2≡ℏ22m(Vd−E)
阱外方程的解为指数函数, 由波函数的有限条件, 可得 x ⩽ d / 2 x \leqslant d / 2 x⩽d/2 和 x ⩾ d / 2 x \geqslant d / 2 x⩾d/2 的两个解为:
ψ ( x ) = { A + e k d x , x ⩽ − d 2 A − e − k d x , x ⩾ d 2 \psi(x)=\left\{\begin{array}{l} A_{+} \mathrm{e}^{k_{d x}}, x \leqslant-\frac{d}{2} \\ A_{-} \mathrm{e}^{-k_{d} x}, x \geqslant \frac{d}{2} \end{array}\right. ψ(x)={
A+ekdx,x⩽−2dA−e−kdx,x⩾2d
式中 k d 、 A ± k_{d} 、 A_{\pm} kd、A±均为常数。
一维方势垒–隧穿效应
粒子从方势垒一端到另一端的穿透概率为
P = e − 2 h 2 m ( V 0 − E ) D P=\mathrm{e}^{-\frac{2}{h} \sqrt{2 m\left(V_{0}-E\right) D}} P=e−h22m(V0−E)D
ln P = − 2 ℏ 2 m ( V 0 − E ) D \ln P=-\frac{2}{\hbar} \sqrt{2 m\left(V_{0}-E\right)} D lnP=−ℏ22m(V0−E)D
D = x 2 − x 1 D=x_{2}-x_{1} D=x2−x1为势垒厚度, V 0 V_0 V0为方势垒的能量,由此可见,势垒厚度 D D D越大,粒子通过的概率越小;粒子的能量 E E E 越大,则穿透概率也越大。
一维谐振子势阱
一维谐振子的势阱能量为: E = p 2 2 m + k x 2 2 E=\frac{p^{2}}{2 m}+\frac{k x^{2}}{2} E=2mp2+2kx2,势能 V ( x ) = 1 2 k x 2 V(x)=\frac{1}{2}kx^2 V(x)=21kx2,令 w = k m w=\sqrt{\frac{k}{m}} w=mk,则对于谐振子势的定态薛定谔方程为:
− ℏ 2 2 m d 2 ψ ( x ) d x 2 + 1 2 m w 2 x 2 ψ ( x ) = E ψ ( x ) -\frac{\hbar^{2}}{2 m} \frac{d^{2} \psi(x)}{d x^{2}}+\frac{1}{2} m w^{2} x^{2} \psi(x)=E \psi(x) −2mℏ2dx2d2ψ(x)+21mw2x2ψ(x)=Eψ(x)
解得:
E n = ( n + 1 2 ) ℏ w ψ n ( x ) = α 2 n n ! π e − α 2 x 2 / 2 H n y \begin{gathered} E_{n}=\left(n+\frac{1}{2}\right) \hbar w \\ \psi_{n}(x)=\sqrt{\frac{\alpha}{2^{n} n ! \sqrt{\pi}}} e^{-\alpha^{2} x^{2} / 2} H_{n} y \end{gathered} En=(n+21)ℏwψn(x)=2nn!παe−α2x2/2Hny
其中 α = m w ℏ , y = α x , H n y \alpha=\sqrt{\frac{m w}{\hbar}}, y=\alpha x, H_{n} y α=ℏmw,y=αx,Hny 为厄密多项式
阅读部分
玻尔理论的问题:为什么驻态(定态)电子不会发射电磁辐射?跃迁时发射和吸收辐射的原因是什么?跃迁时电子已经离开 E 1 E_1 E1态尚未到达 E 2 E_2 E2态,这时电子处于什么状态呢?
经典力学中测量波的频率和波长也有关系式: Δ x Δ λ ≥ λ 2 \Delta x \Delta \lambda \ge \lambda^2 ΔxΔλ≥λ2,要无限准确的测准频率就需花费无限长的时间,要无限准确的测准波长,就必须在无限扩展的空间中观察。
戴维逊-革末实验
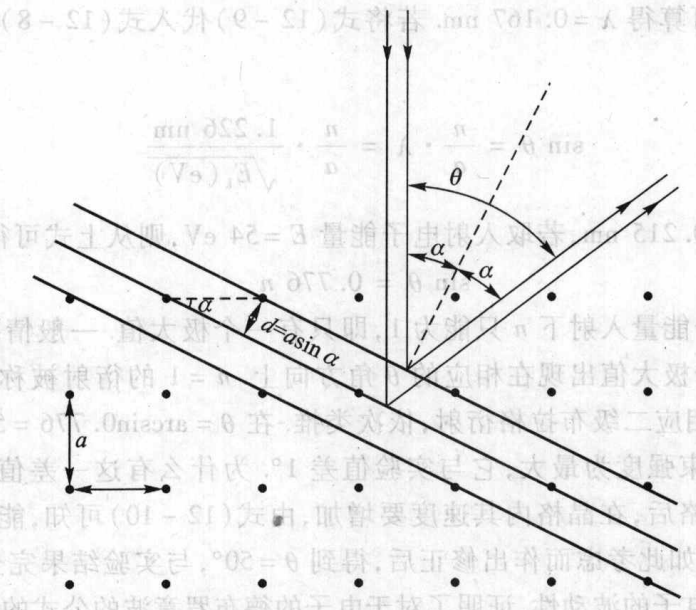
电子在晶体中的散射是射线在晶格中散射的一个特例,这时的散射平面既是一个镜面,又是一个晶面,这种面被称为布拉格面,所产生的的衍射称为布拉格衍射。在下图中,横竖晶格常数都为 a a a,入射与出射的夹角均为 θ \theta θ,图中的 a = θ 2 a=\frac{\theta}{2} a=2θ,两相邻布拉格面的间距 d = a sin α d=a\sin{\alpha} d=asinα,这样强波束射出的条件是 n λ = 2 d cos α = a sin θ n\lambda = 2d\cos{\alpha}=a\sin{\theta} nλ=2dcosα=asinθ。

德布罗意波和量子态
德布罗意把角动量量子化条件 L = n ℏ L=n\hbar L=nℏ 作为假设,去推导其它物理量。
德布罗意假设认为,体现电子波动性的波长为 λ = h p = h m v \lambda=\frac{h}{p}=\frac{h}{mv} λ=ph=mvh,现在把这个关系用回氢原子中,则要是绕核运动的电子稳定存在,电子对应的波必须是一个驻波。
刚性匣子中的粒子,匣子长度为 d d d,匣子壁是驻波的波节 d = n λ 2 d=n\frac{\lambda}{2} d=n2λ --> p = n h 2 d p=\frac{nh}{2d} p=2dnh,粒子动能 E k = p 2 2 m = n 2 h 2 8 m d 2 E_k=\frac{p^2}{2m}=\frac{n^2h^2}{8md^2} Ek=2mp2=8md2n2h2 束缚粒子的能量是量子化的。
将匣子等效为核的库仑电势,其中的粒子就是电子,电子沿轨道一周后应回到原点,所以轨道长应为匣长的2倍, d = π r d=\pi r d=πr,所以电子动能 E k = n 2 h 2 8 m π 2 r 2 E_k=\frac{n^2h^2}{8m\pi^2 r^2} Ek=8mπ2r2n2h2,势能 E p = − e 2 4 π ε 0 r E_p=-\frac{e^2}{4\pi \varepsilon_0 r} Ep=−4πε0re2,总能量 E = E k + E p = n 2 h 2 8 m π 2 r 2 − − e 2 4 π ε 0 r E=E_k+E_p=\frac{n^2h^2}{8m\pi^2 r^2}--\frac{e^2}{4\pi \varepsilon_0 r} E=Ek+Ep=8mπ2r2n2h2−−4πε0re2,能量最小值有 d E d r = 0 \frac{dE}{dr}=0 drdE=0,由此关系得 r m i n = ( e 2 4 π ε 0 − 1 ) h 2 4 π 2 m = 4 π ε 0 ℏ 2 m e e 2 = a 1 r_{min}=(\frac{e^2}{4\pi\varepsilon_0}^{-1}) \frac{h^2}{4\pi^2m}=\frac{4 \pi \varepsilon_{0} \hbar^{2}}{m_{\mathrm{e}} e^{2}}=a_1 rmin=(4πε0e2−1)4π2mh2=mee24πε0ℏ2=a1, E m i n = ⋯ = − 13.6 e V E_{min}=\dots=-13.6eV Emin=⋯=−13.6eV,我们很自然地推出原子世界中最重要的特征量线度 a 1 a_1 a1和能量 E E E,因此物质的波粒二象性的假设是正确的,波粒二象性是量子力学理论的基础。
我们先考察一下辐射的情况,静电理论告诉我们,电磁波的能量流(单位时间上的能量大小)正比于波的电场强度平方 KaTeX parse error: Undefined control sequence: \abs at position 1: \̲a̲b̲s̲{E}^2;从粒子角度看,它应等于 h ν N h\nu N hνN,其中 N N N是光子的通量,即单位时间垂直于传播方向的单位面积电子数。计算时发现 N N N可以是小数,又因光子是量子化的,这说明 N N N应当是平均值,表示一个光子在单位时间内穿过单位面积的概率的量度。
一定频率的光的强度与光子数成正比,某一处的光子数与该处出现光子的概率成正比,所以 N ∝ ∣ E ∣ 2 N \propto|\boldsymbol{E}|^{2} N∝∣E∣2,我们知道,波长为 λ \lambda λ、频率为 ν \nu ν、在 x x x方向运动的正弦电磁波的电场强度可以写作: E = E 0 sin 2 π ( x λ − ν t ) E=E_{0} \sin 2 \pi\left(\frac{x}{\lambda}-\nu t\right) E=E0sin2π(λx−νt),而对于在 x x x 方向以恒定线动量运动的粒子,其德布罗意波可相应地写为
ψ = ψ 0 sin 2 π ( x λ − ν t ) \psi=\psi_{0} \sin 2 \pi\left(\frac{x}{\lambda}-\nu t\right) ψ=ψ0sin2π(λx−νt)
或者,更一般地写为: ψ = ψ 0 e i ( k + r − ω t ) \psi=\psi_0 e^{i(k+r-\omega t)} ψ=ψ0ei(k+r−ωt),式中 ∣ k ∣ = 2 π / λ , ω = 2 π ν |\boldsymbol{k}|=2 \pi / \lambda, \omega=2 \pi \nu ∣k∣=2π/λ,ω=2πν。这样,与物质波相联系的不仅有一个波长,而且还有一个振幅 ψ \psi ψ,称之为波函数。类似于爱因斯坦把 ∣ E ∣ 2 |E|^{2} ∣E∣2 解释为 “光子密度的概率量度”,玻恩把 ∣ ψ ∣ 2 |\psi|^{2} ∣ψ∣2 解释为在给定时间、在 r \boldsymbol{r} r 处的单位体积中发现一个粒子的概率。玻恩提出的波函数的概率解释是量子力学的基本原理之一,也可以说是一个基本假设。经典的波振幅可测,而 ψ \psi ψ一般不可测,能测得的知识KaTeX parse error: Undefined control sequence: \abs at position 1: \̲a̲b̲s̲{\psi}^2,它的含义是概率。
今天的文章 量子力学导论分享到此就结束了,感谢您的阅读。粒子的康普顿波长为: λ c = h / m 0 c \lambda_c=h/m_0c λc=h/m0c

版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/bian-cheng-ji-chu/84577.html