吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记（5-1）-- 循环神经网络

作者：大树先生
博客：吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记（5-1）-- 循环神经网络
知乎：https://www.zhihu.com/people/dashuxiansheng
GitHub：https://github.com/KoalaTree
2018 年 3 月 3 日

Ng最后一课发布了，撒花！以下为吴恩达老师 DeepLearning.ai 课程项目中，第五部分《序列模型》第一周课程“循环神经网络”关键点的笔记。

同时我在知乎上开设了关于机器学习深度学习的专栏收录下面的笔记，以方便大家在移动端的学习。欢迎关注我的知乎：大树先生。一起学习一起进步呀！^_

序列模型 — 循环神经网络

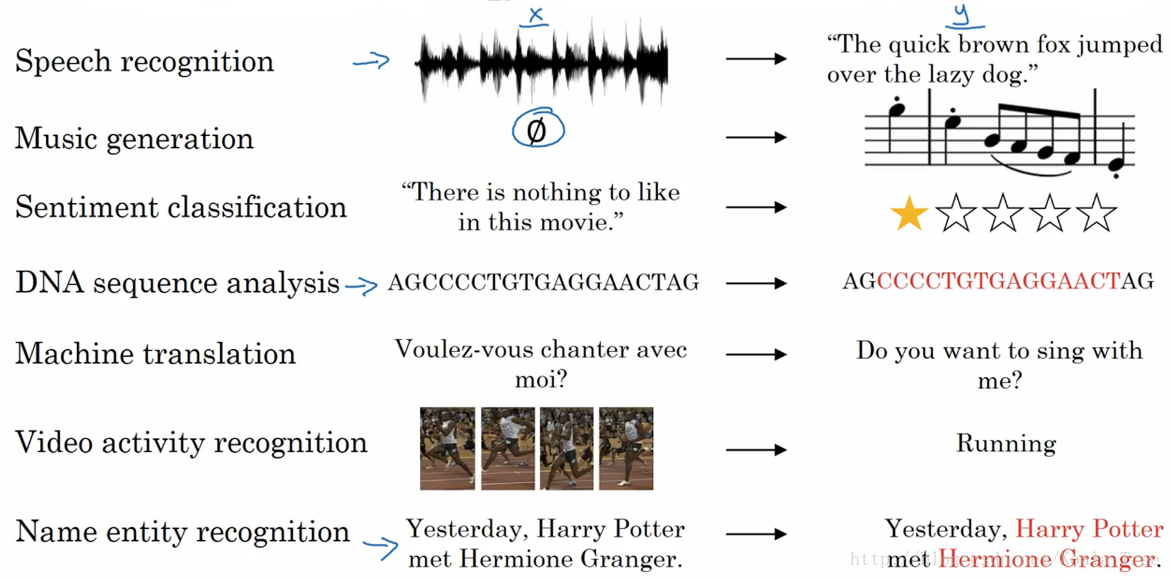
1. 序列模型的应用

语音识别：将输入的语音信号直接输出相应的语音文本信息。无论是语音信号还是文本信息均是序列数据。
音乐生成：生成音乐乐谱。只有输出的音乐乐谱是序列数据，输入可以是空或者一个整数。
情感分类：将输入的评论句子转换为相应的等级或评分。输入是一个序列，输出则是一个单独的类别。
DNA序列分析：找到输入的DNA序列的蛋白质表达的子序列。
机器翻译：两种不同语言之间的想换转换。输入和输出均为序列数据。
视频行为识别：识别输入的视频帧序列中的人物行为。
命名实体识别：从输入的句子中识别实体的名字。

2. 数学符号

输入x：如“Harry Potter and Herminone Granger invented a new spell.”(以序列作为一个输入)， $x^{<t>}$ 表示输入x中的第t个符号。
输出y：如“1 1 0 1 1 0 0 0 0”（人名定位），同样，用 $y^{<t>}$ 表示输出y中的第t个符号。
$T_{x}$ 用来表示输入x的长度；
$T_{y}$ 用来表示输出y的长度；
$x^{(i)<t>}$ 表示第i个输入样本的第t个符号，其余同理。
利用单词字典编码来表示每一个输入的符号：如one-hot编码等，实现输入x和输出y之间的映射关系。

3. 循环神经网络模型

传统标准的神经网络：

对于学习X和Y的映射，我们可以很直接的想到一种方法就是使用传统的标准神经网络。也许我们可以将输入的序列X以某种方式进行字典编码以后，如one-hot编码，输入到一个多层的深度神经网络中，最后得到对应的输出Y。如下图所示：

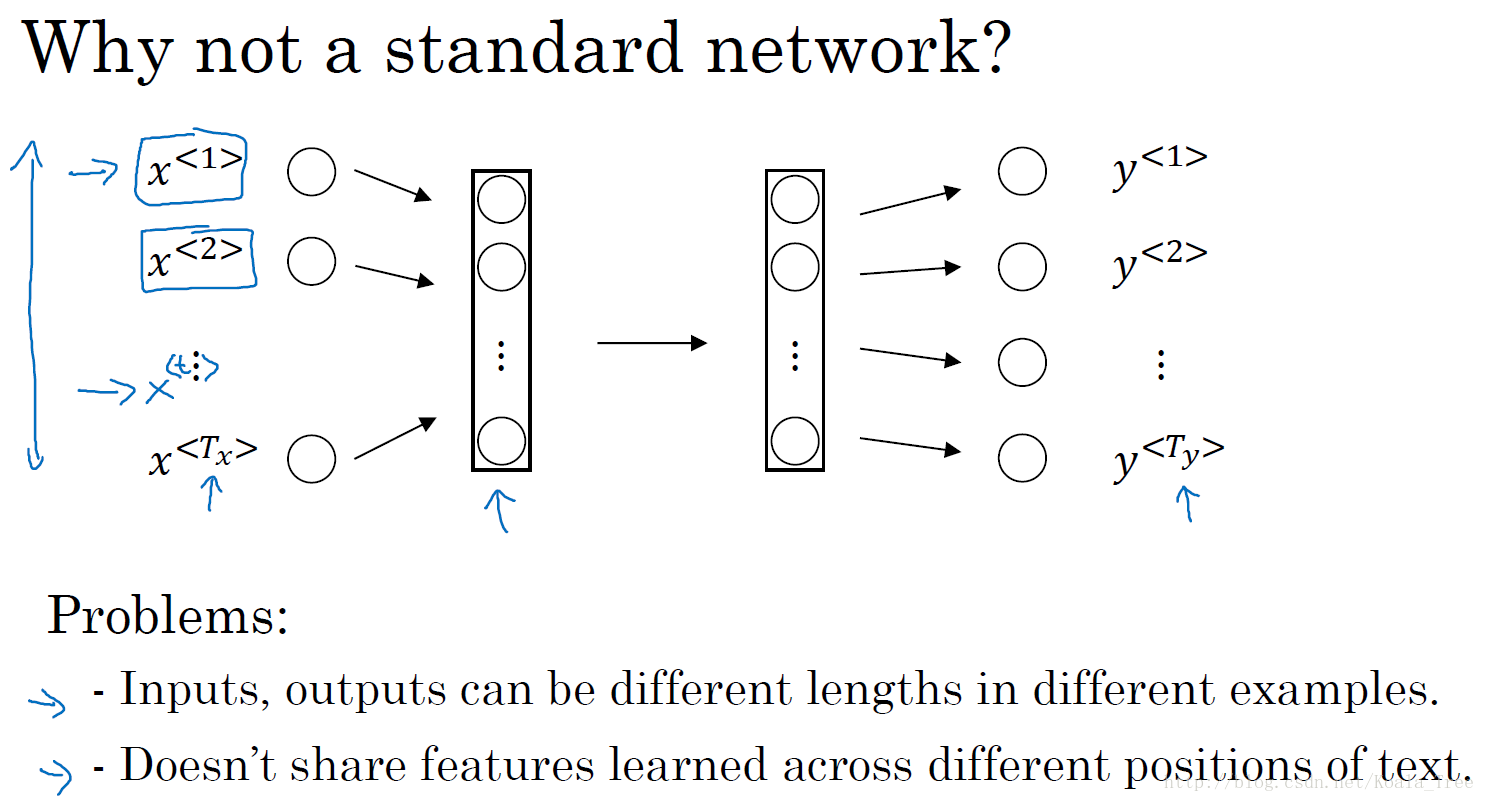
但是，结果表明这种方法并不好，主要是存在下面两个问题：

输入和输出数据在不同的例子中可以有不同的长度；
这种朴素的神经网络结果并不能共享从文本不同位置所学习到的特征。（如卷积神经网络中学到的特征的快速地推广到图片其他位置）

循环神经网络：

循环神经网络作为一种新型的网络结构，在处理序列数据问题上则不存在上面的两个缺点。在每一个时间步中，循环神经网络会传递一个激活值到下一个时间步中，用于下一时间步的计算。如下图所示：

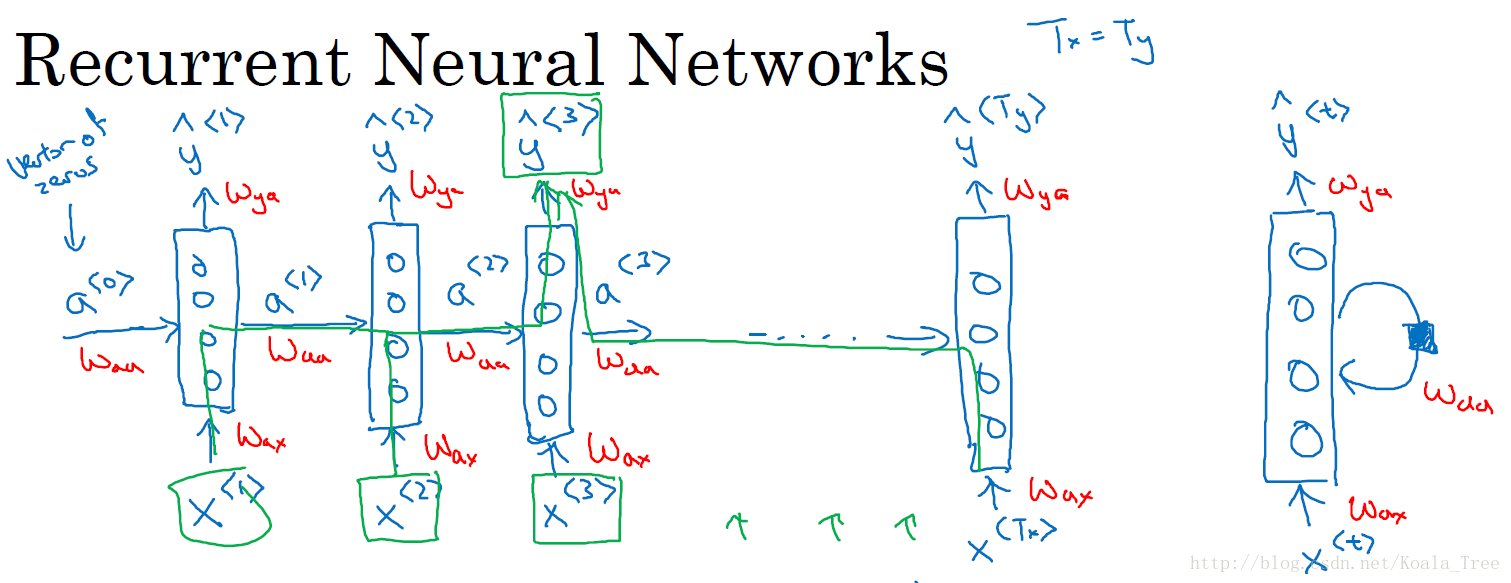
这里需要注意在零时刻，我们需要编造一个激活值，通常输入一个零向量，有的研究人员会使用随机的方法对该初始激活向量进行初始化。同时，上图中右边的循环神经网络的绘制结构与左边是等价的。

循环神经网络是从左到右扫描数据的，同时共享每个时间步的参数。

$W_{ax}$ 管理从输入 $x^{<t>}$ 到隐藏层的连接，每个时间步都使用相同的 $W_{ax}$ ，同下；
$W_{aa}$ 管理激活值 $a^{<t>}$ 到隐藏层的连接；
$W_{ya}$ 管理隐藏层到激活值 $y^{<t>}$ 的连接。

上述循环神经网络结构的缺点：每个预测输出 $y^{<t>}$ 仅使用了前面的输入信息，而没有使用后面的信息。Bidirectional RNN（双向循环神经网络）可以解决这种存在的缺点。

循环神经网络的前向传播：

下图是循环神经网络结构图：

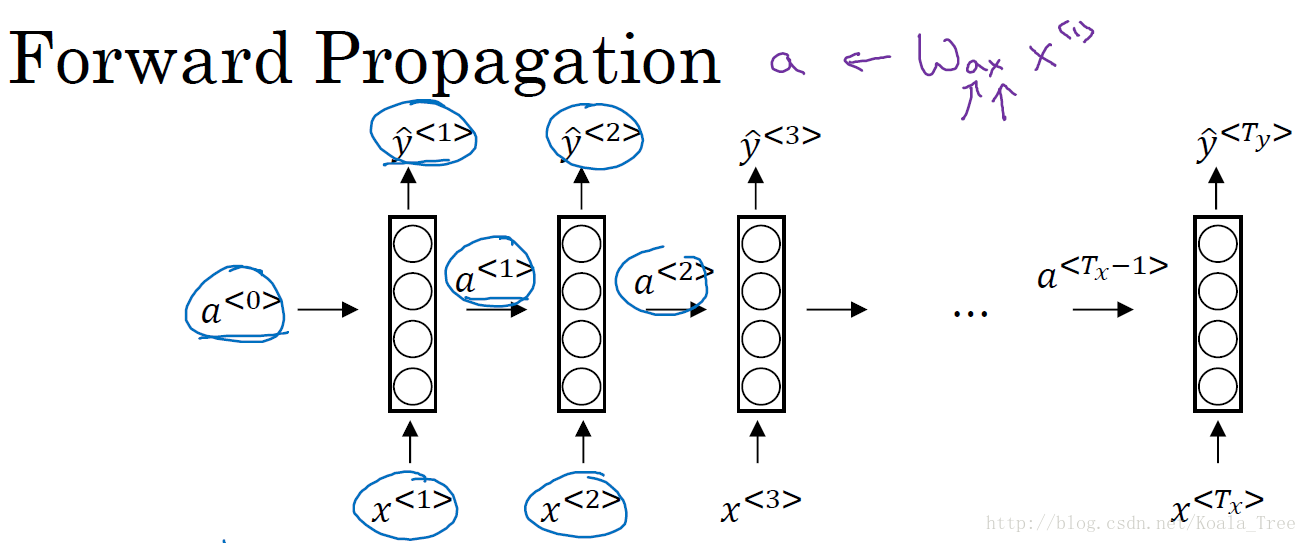
构造初始激活向量：$a^{<0>} = \overrightarrow {0} $；
$a^{<1>} = g(W_{aa}a^{<0>}+W_{ax}x^{<1>}+b_{a})$ ;通常选择 $t a n h$ 作为激活函数，有时也会使用 $R e l u$ 作为激活函数；（使用tanh函数梯度消失的问题会用其他方式解决）
$\hat y^{<1>} = g(W_{ya}a^{<1>}+b_{y})$ ；如果是二分类问题，使用sigmoid作为激活函数，如果是多分类问题，可以使用softmax激活函数；
注：其中 $W_{ax}$ 中，前面的 $a$ 表示要得到一个 $a$ 类型的量， $x$ 表示参数 $W$ 要乘以一个 $x$ 类型的量，其余 $W_{aa}$ 、 $W_{ya}$ 同理；
$a^{<t>} = g(W_{aa}a^{<t-1>}+W_{ax}x^{<t>}+b_{a})\\ \hat y^{<t>} = g(W_{ya}a^{<t>}+b_{y})$

今天的文章吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记（5-1）-- 循环神经网络分享到此就结束了，感谢您的阅读。

吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记（5-1）-- 循环神经网络

序列模型 — 循环神经网络

1. 序列模型的应用

2. 数学符号

3. 循环神经网络模型

相关推荐