文章目录
前言
在计算机科学与编程领域,循环结构作为程序设计的基础构件之一,对于实现重复执行某段代码逻辑至关重要。特别是当涉及到数值处理、数据遍历、或是模式生成等场景时,循环结构的运用尤为关键。本篇文章深入探讨了循环结构中一个核心概念——带余除法,及其在C++编程中的广泛应用。带余除法不仅在基本的数学运算中扮演着重要角色,更是众多高级算法与数据处理逻辑的基石。通过理解并掌握这一概念,编程新手能够迈出坚实的一步,向更复杂的算法设计与问题解决能力迈进。
学习路线:C++从入门到NOI学习路线
学习大纲:C++全国青少年信息学奥林匹克竞赛(NOI)入门级-大纲
一、带余除法
1.1 概念
带余除法,也称为除法的带余形式,是指当我们对两个整数进行除法运算时,得到的结果不仅包括商,还包括余数。具体来说,如果有一个整数被另一个非零整数除,结果可以表示为:
a = bq + r 其中:
- a 是被除数(dividend),
- b 是除数(divisor),且 𝑏≠0,
- q 是商(quotient),它是整除的结果,
- r 是余数(remainder),满足 0 ≤ r < ∣b∣。
这意味着,任何整数 a 除以非零整数 b 的结果可以分解为一个整数商 q 加上一个小于除数绝对值的余数 r。如果r=0,则说明 a 能被 b 整除。
1.2 编程中的使用
1.2.1 模运算
模运算(% )直接体现了带余除法的余数部分,常用于处理周期性问题、取模运算等。
例如:
#include <iostream> using namespace std; int main() {
for(int day = 1; day <= 7; ++day) {
cout << "今天是第 " << day << " 天" << endl; if(day % 7 == 0) {
cout << "一周结束,周末快乐!" << endl; } } } return 0; } 通过循环模拟一周七天的过程。使用模运算day % 7来检测是否到达一周的末尾(即余数为0时),从而在每个星期日输出“周末快乐!”的消息。这演示了模运算在处理循环和周期性事件中的应用。
1.2.2 判断奇偶性
通过 n % 2 可以简单判断一个整数 n 是否为奇数(余数为1则为奇数,为0则为偶数)。
例如:
#include <iostream> using namespace std; int main() {
int number = 7; if(number % 2 == 0) {
cout << number << " 是偶数。" << endl; } else {
cout << number << " 是奇数。" << endl; } return 0; } 判断一个整数的奇偶性实质上是带余除法中模运算的一个直接应用。当我们对任意整数 n 使用模运算 % 2 时,就是在做带余除法,即 n = 2*q + r,其中 q 是商,而 r 是余数。在这种情况下,余数 r 只可能为0或1,因为2是偶数,任何整数除以2的余数只能是这两个值之一。
1.2.3 判断倍数关系
判断 n 是否是 m 的倍数,可以使用 n % m == 0。如果这个表达式为真,意味着 n 能被 m 整除,即 n 是 m 的倍数。
例如:
#include <iostream> using namespace std; int main() {
int n = 12, m = 3; if(n % m == 0) {
cout << n << " 是 " << m << " 的倍数。" << endl; } else {
cout << n << " 不是 " << m << " 的倍数。" << endl; } return 0; } 使用n % m == 0来检查n是否能被m整除,即n是否为m的倍数。当余数为0时,表明n能被m整除,证明了它们之间存在倍数关系。此例展现了模运算在判断数与数之间整除性质上的应用。
1.2.4 循环和迭代控制
在需要循环一定次数或者按固定间隔执行某些操作时,模运算可以帮助我们控制循环的流程。
例如:
#include <iostream> using namespace std; int main() {
for(int i = 0; i < 20; ++i) {
cout << "*"; if((i+1) % 10 == 0) {
// 每10个星号后换行 cout << endl; } } } return 0; } 本例中,循环打印星号,并在每满10个星号后换行,通过(i+1) % 10 == 0来判断何时应该换行。这展示了模运算如何帮助控制循环的流程,实现特定的输出格式或规律性行为。
1.2.5 密码学与安全
在密码学中,模运算是构建很多加密算法(如RSA加密)的基础,其中带余除法的概念是理解这些算法的关键。
例如:
#include <iostream> using namespace std; int main() {
// 简化的RSA示例,仅展示模幂运算 int base = 5, exponent = 3, modulus = 13; int result = 1; for(int i = 0; i < exponent; ++i) {
result = (result * base) % modulus; } cout << "计算结果: " << result << endl; return 0; } 简化版的RSA示例展示了模幂运算,通过循环和模运算计算base的exponent次方对modulus取模的结果。模运算在此类加密算法中用于保持运算结果的范围,同时保证运算的安全性和隐私保护,是密码学中的基础工具。
1.2.6 算法设计
许多经典的算法,如欧几里得算法(GCD求解)和中国剩余定理的应用,都依赖于带余除法的原理。
例如:
#include <iostream> using namespace std; int gcd(int a, int b) {
while(b != 0) {
int t = b; b = a % b; a = t; } return a; } int main() {
int x = 48, y = 18; cout << "GCD of " << x << " and " << y << " is " << gcd(x, y) << endl; return 0; } 使用模运算实现欧几里得算法,通过循环不断更新a和b的值,直到b变为0,此时a即为两数的最大公约数。此例展示了模运算在经典算法设计中的核心作用,尤其是解决数论问题。
1.2.7 数据验证与错误处理
在处理数组索引等场合,使用模运算可以确保索引值在有效范围内,防止越界错误。
例如:
#include <iostream> using namespace std; void accessArray(int arr[], int size, int index) {
// 使用模运算确保索引在有效范围内 int safeIndex = index % size; cout << "数组索引为: " << safeIndex << ", 数组值为: " << arr[safeIndex] << endl; } int main() {
int arr[] = {
1, 2, 3, 4, 5}; int size = sizeof(arr)/sizeof(arr[0]); accessArray(arr, size, 7); // 实际索引超出范围,但通过模运算避免错误 return 0; } 该示例通过index % size确保数组访问的安全性,即使提供的索引值大于数组的实际大小,也能通过模运算得到一个合法的索引值,防止数组越界错误。这说明了模运算在数据验证和错误预防中的实用性,确保程序的健壮性。
二、例题讲解
问题:1389 - 数据分析
类型:简单循环
题目描述:
该方法的操作方式为,如果要传递 2 个数字信息给友军,会直接传递给友军一个整数 n(n 是一个 10 位以内的整数),该整数的长度代表要传递的第一个数字信息,分解出该整数的每一位,如果该位是偶数,那么将这一位加到总和上去,代表要传递的第二个数字信息。
请你编写一个程序,从接收到的数字 n 中获取这 2 个数字信息。
比如:军事单位传递的数字为 ,则希望向友军传递的 2 个数字就是 8 (共有 8 位)和 20(2+4+6+8=20) 。
输入:
一个整数 n(n≤10^9 ) 。
输出:
两个整数,用空格隔开。
样例:
输入:
输出:
8 20 
1.分析问题
- 已知:一个整数n;
- 未知:数字n中的 2 个数字信息。
- 关系:长度代表要传递的第一个数字信息,各数位上偶数的总和
2.定义变量
- 定义整型变量n用于存储输入的整数,t作为临时变量存储n的每一位数字,one用于记录位数,two用于记录偶数位的总和。
//二、数据定义 int n,t,one=0,two=0; 3.输入数据
- 读取用户输入的整数n。
//三、数据输入 cin>>n; 4.数据计算
使用while(n)循环,只要n不为0就继续执行循环。
- t = n % 10; 取n的个位数存入t。
- if(t % 2 == 0) 判断t是否为偶数,如果是则执行two += t;累加到偶数总和中。
- n /= 10; 通过整除10去除n的个位,使n的值向左移一位,以便下一次循环处理下一位数字。
- ++one; 每次循环增加1,用于计数位数。
//四、数据计算 while(n){
t=n%10; if(t%2==0){
two+=t; } n/=10; ++one; } 5.输出结果
- 输出位数和偶数位数字的总和,中间用空格隔开。
//五、输出结果 cout<<one <<" "<<two; 完整代码如下:
#include<bits/stdc++.h> // 引入头文件,包含了所有常用STL库函数,方便编程但可能降低编译速度,实际开发中推荐按需引入具体头文件。 using namespace std; // 声明使用标准命名空间std,使得可以直接调用std下的函数和对象,如cin, cout等,无需前缀std::。 int main(){
// 定义主函数,程序的入口点。 // 分析问题 // 已知:一个整数n; // 未知:要找出两个关于n的信息——数字n的位数(长度)和n中所有偶数位数字的总和。 // 数据定义 int n, t, one = 0, two = 0; // 定义变量:n为待处理的整数,t为临时变量存储n的当前位数,one记录位数,two记录偶数位总和。 // 数据输入 cin >> n; // 从标准输入读取一个整数n。 // 数据计算 while(n){
// 当n不等于0时,继续循环。 t = n % 10; // 取n的个位数存入t。 if(t % 2 == 0){
// 判断t(当前位数)是否为偶数。 two += t; // 若是偶数,将其加到two中。 } n /= 10; // n除以10丢弃个位,让其变为下一个位的数。 ++one; // 位数计数加1,表示处理了一位。 } // 输出结果 cout << one << " " << two; // 打印出位数(one)和偶数位数字的总和(two),中间以空格分隔。 return 0; // 主函数结束,返回0表示程序正常退出。 } 问题:1750 - 有0的数
类型:简单循环
题目描述:
请求出 1∼n 中含有数字 0 的数,有多少个?
输入:
一个整数 n(n≤999) 。
输出:
一个整数,代表 1∼n 中含有数字 0 的数的个数。
样例:
输入:
80 输出:
8 
1.分析问题
- 已知:1-n的数 (n<=999);
- 未知:含0的数的个数;
- 关系:带余除法
2.定义变量
- 定义整型变量n用于接收用户输入的上限值,c初始化为0,用来计数含0的数字数量。
//二、数据定义 int n,c=0; 3.输入数据
- 从标准输入读取一个整数n,作为计数范围的上限。
//三、数据输入 cin>>n; 4.数据计算
通过for循环遍历10到n(含n)之间的每个数i。
- 判断条件i%10==0检查i的个位是否为0;
- 判断条件i/10%10==0检查i的十位是否为0(先整除后取余,确保检查十位);
- 如果i的个位或十位包含0,则c的值增加1,表示找到了一个含0的数字。
//四、数据计算 for(int i=10;i<=n;i++){
if(i%10==0||i/10%10==0) ++c; } 5.输出结果
- 将统计得到的含0数字的数量c输出到标准输出。
//五、输出结果 cout<<c; return 0; 完整代码如下:
#include<bits/stdc++.h> // 包含通用头文件,提供多种常用库函数 using namespace std; // 使用std命名空间,简化标准库函数的调用 int main() {
// 程序执行入口 // 问题描述: // 给定一个正整数n,计算从1到n之间(包括n)数字中包含数字0的个数。 // 方法:通过逐个检查每个数的个位和十位是否为0来计数。 int n, count = 0; // 初始化变量,n为用户输入值,count记录含0的数的总数 // 用户输入 cin >> n; // 循环处理:从10开始至n(包括n) for(int i = 10; i <= n; i++) {
// 检查当前数的个位或十位是否为0 if(i % 10 == 0 || i / 10 % 10 == 0) count++; // 是,则count加1 } // 输出结果 cout << count; // 输出含0的数字总数 return 0; // 程序成功执行完毕,返回0 } 问题:1457 - 子数整除
类型:循环应用
题目描述:
于一个五位数 abcde ,可将其拆分为三个子数:
sub1=abc
sub2=bcd
sub3=cde
例如,五位数20207 可以拆分成sub1=202
sub2=020 (也就是 20)
sub3=207
现在给定一个正整数 K ,要求你编程求出 10000 到30000 之间所有满足下述条件的五位数,条件是这些五位数的三个子数sub1,sub2,sub3 都可被 K 整除。
输入:
一个正整数K(0<K<1000) 。
输出:
样例:
输入:
15 输出:
22555 25555 28555 30000 
1.分析问题
- 已知:10000-30000的五位数,正整数K
- 未知:哪些五位数的三个子数sub1,sub2,sub3都可被K整除。
- 关系:一个五位数abcde,可将其拆分为三个子数:sub1=abc,sub2=bcd,sub3=cde
2.定义变量
- 定义变量k用于存储用户输入的整数,sub1、sub2、sub3分别存储五位数分解出的三个子数。
- isFind,表示是否找到了符合条件的数。
//二、数据定义 int k,sub1,sub2,sub3; bool isFind=false; 3.输入数据
- 读取用户输入的正整数K。
//三、数据输入 cin>>k; 4.数据计算
通过一个for循环遍历从10000到30000的所有五位数。
- 计算每个五位数对应的sub1、sub2、sub3,方法是通过数学运算提取相应位置的数字。
- 判断这三个子数是否都能被K整除,如果能则打印该五位数,并设置isFind为true表示找到了至少一个解。
//四、数据计算 for(int i=10000;i<=30000;i++){
sub1=i/100; sub2=i/10%1000; sub3=i%1000; if(sub1%k==0&&sub2%k==0&&sub3%k==0){
if(!isFind) isFind=true; cout<<i<<endl; } } 5.输出结果
- 如果没有找到任何符合条件的数(即isFind仍为false),则输出"No"。
//五、输出结果 if(!isFind){
cout<<"No"; } 完整代码如下:
#include <bits/stdc++.h> // 包含常用头文件 using namespace std; int main() {
// 问题分析: // 给定条件:寻找10000至30000之间,能被用户输入的正整数K整除其特定子串的所有五位数。 // 子串定义:将五位数分为abcde,子串为abc、bcd、cde。 // 数据定义 int k, sub1, sub2, sub3; // k为用户输入的整数,sub1、sub2、sub3分别为五位数的子串 bool isFind = false; // 标记是否找到符合条件的五位数 // 数据输入 cin >> k; // 读取用户输入的K值 // 数据计算 for (int i = 10000; i <= 30000; i++) {
// 遍历10000至30000之间的所有五位数 sub1 = i / 100; // 提取五位数的前三位(abc) sub2 = (i / 10) % 1000; // 提取五位数的中间三位(bcd),先除以10移除个位,再取模1000保留后三位 sub3 = i % 1000; // 提取五位数的后三位(cde),直接对1000取余 // 检查这三个子串是否都能被K整除 if (sub1 % k == 0 && sub2 % k == 0 && sub3 % k == 0) {
// 如果是第一个找到的解,标记已找到解 if (!isFind) isFind = true; cout << i << endl; // 打印当前找到的满足条件的五位数 } } // 输出结果 // 如果没有找到任何满足条件的五位数 if (!isFind) {
cout << "No"; // 输出"No" } return 0; // 程序正常结束 } 问题:1121 - “倒”数
类型:需要找规律的循环
题目描述:
输入:
一行,一个正整数 N 。
输出:
一行,一个正整数。
样例:
输入:
345 输出:
543 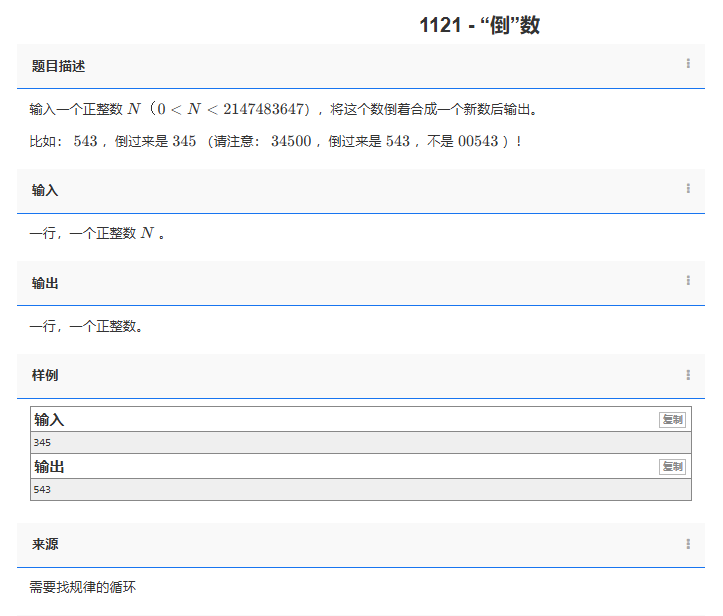
1.分析问题
- 已知:一个正整数n(0<n<);
- 未知:输出它的倒数;
- 关系:带余除法。
2.定义变量
- 定义了两个整型变量,n用于存储输入的整数,result初始化为0,用于存放颠倒后的结果。
//二、数据定义 int n,result=0; 3.输入数据
- 通过cin读取用户输入的整数n。
//三、数据输入 cin>>n; 4.数据计算
- 使用while循环,在每次迭代中,将n的最后一个数字(通过n % 10获得)加到result的末尾(通过result * 10 + n % 10实现),同时去掉n的最后一个数字(通过n /= 10实现)。
- 循环直至n变为0,此时result中存储的就是原数的数字顺序颠倒后的结果。
//四、数据计算 while(n!=0){
result=result*10+n%10; n/=10; } 5.输出结果
- 使用cout输出结果result。
//五、输出结果 cout<<result; 完整代码如下:
#include<iostream> using namespace std; int main(){
// 一、问题分析 // 给定条件:一个正整数n,其值位于0到之间(不包括0)。 // 目标:输出该整数的数字顺序颠倒后的结果。 // 方法:使用带余数的除法逐步提取原数的每一位数字,并将其累加到结果变量以构建颠倒后的数字。 // 二、数据定义 int n, result = 0; // n 用于存储输入的整数,result 初始化为0,用于存放最终的颠倒结果 // 三、数据输入 cin >> n; // 从标准输入读取一个整数到变量n中 // 四、数据计算 while(n){
// 当n不为0时,继续处理 result = result * 10 + n % 10; // 将n的最后一个数字添加到result的末尾 n /= 10; // 去掉n的最后一个数字 } // 五、输出结果 cout << result << endl; // 输出颠倒后的数字 return 0; // 程序结束,返回0表示成功执行 } 问题:1962. 数值计算
类型:简单循环
题目描述:
给出一个不多于 5 位的非负整数,要求
1、 求出它是几位数
2、 分别输出每一位数字
3、 按逆序输出各位数字,例如原数为 321 ,应输出 123。
输入:
一个不大于 5 位的正整数。
输出:
三行
第 1 行 5 位数。
第 2 行 用空格分开的每个数字。
第 3 行 按逆序输出这个数。
样例:
输入:
12345 输出:
5 1 2 3 4 5 54321 
1.分析问题
- 已知:一个不多于 5 位的非负整数;
- 未知:求出它是几位数; 分别输出每一位数字;按逆序输出各位数字;
2.定义变量
- 定义了三个变量,n用于存储输入的整数,c用于计数位数,dx用于存储逆序整数。
//二、数据定义 int n,c=0,dx=0; 3.输入数据
- 使用cin读取用户输入的整数。
//三、数据输入 cin>>n; 4.数据计算
- 通过一个while循环处理输入的整数n。在循环中,我们递增c以计数位数,同时逐步构建逆序数dx。每次循环,temp除以10并向下取整,直到temp变为0,循环结束。
int temp=n; while(temp){
++c; dx=dx*10+temp%10; temp/=10; } 5.输出结果
- 首先输出整数的位数c。
- 接着,通过将dx(逆序数)逐位输出,实际上实现了原整数的正序输出。因为对逆序数dx从低到高逐位处理,恰好等同于原数的正序遍历。
- 最后,再次输出逆序数dx。
//五、输出结果 cout<<c<<endl; temp=dx; while(temp){
cout<<temp%10<<" "; temp/=10; } cout<<endl<<dx; 完整代码如下:
#include <bits/stdc++.h> // 包含常用头文件,简化代码 using namespace std; // 使用std命名空间,避免std::前缀 int main() {
// 问题分析: // 给定一个最多5位的非负整数,需完成以下任务: // 1. 计算该整数的位数。 // 2. 分别输出每一位数字(正序)。 // 3. 按逆序输出每一位数字。 // 数据定义: int n, c = 0, dx = 0; // n: 用户输入的整数; c: 记录位数; dx: 用于存储逆序后的整数 // 数据输入: cin >> n; // 从标准输入读取一个非负整数 // 数据处理: int temp = n; // 创建临时变量temp,用于迭代处理n while(temp) {
// 当temp不为0时循环 ++c; // 每次循环增加c的值,用于计数位数 dx = dx * 10 + temp % 10; // dx通过当前最低位数字构建逆序数(当前位*10+新低位) temp /= 10; // temp除以10丢弃当前最低位,继续处理下一位 } // 输出结果: cout << c << endl; // 输出整数的位数 // 准备正序输出数字,通过逆序数dx间接实现 temp = dx; // 将dx的值赋给temp,开始正序输出每一位 while(temp) {
// 对temp进行循环,直到所有位都输出 cout << temp % 10 << " "; // 输出当前最低位数字,然后加空格分隔 temp /= 10; // 移动到下一个更高位 } cout << endl; // 输出换行,分隔正序与逆序输出部分 cout << dx << endl; // 再次输出dx,展示逆序后的整数 return 0; // 程序正常结束 } 三、总结
通过对带余除法及其在C++编程中的应用进行全面解析,我们不仅重温了其基本概念,还深入探讨了模运算在多个维度上的重要性。从简单的周期性问题处理、奇偶性判断,到倍数关系验证、循环控制、乃至深入密码学与算法设计的核心,模运算展示了其强大的灵活性与实用性。通过一系列实例,我们见证了如何利用带余除法解决实际问题,比如数据反转、数字分析、以及安全相关的应用等。此外,模运算在确保程序健壮性,如数组索引验证方面,也发挥了不可小觑的作用。
通过学习和实践这些例子,读者应已掌握了如何在循环结构中有效地运用带余除法,进一步理解了它在处理循环逻辑、数据验证、算法设计等方面的价值。这对于准备参加NOI(全国青少年信息学奥林匹克竞赛)及其他编程相关比赛的学生而言,无疑是宝贵的技能提升。未来无论是面对数学计算、数据处理,还是解决更复杂数学问题和算法设计挑战,带余除法及其在循环结构中的应用都将是一把不可或缺的钥匙。希望本次学习之旅能够激发更多对编程和算法探索的兴趣,助力每一位学习者在信息技术的海洋中扬帆远航。
四、感谢
如若本文对您的学习或工作有所启发和帮助,恳请您给予宝贵的支持——轻轻一点,为文章点赞;若觉得内容值得分享给更多朋友,欢迎转发扩散;若认为此篇内容具有长期参考价值,敬请收藏以便随时查阅。
每一次您的点赞、分享与收藏,都是对我持续创作和分享的热情鼓励,也是推动我不断提供更多高质量内容的动力源泉。期待我们在下一篇文章中再次相遇,共同攀登知识的高峰!


版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/bian-cheng-ji-chu/88898.html