OpenCV学习(十九) ：图像的矩:moments()，HuMoments()

参考博客：
图像的矩特征
Structural Analysis and Shape Descriptors：opencv 形态描述
【图像算法】图像特征：几何不变矩–Hu矩
如何理解概率论的“矩”？

一、概述

1、图像识别的一个核心问题是图像的特征提取，简单描述即为用一组简单的数据(数据描述量)来描述整个图像，这组数据月简单越有代表性越好。良好的特征不受光线、噪点、几何形变的干扰，图像识别技术的发展中，不断有新的描述图像特征提出，而图像不变矩就是其中一个。
2、从图像中计算出来的矩通常描述了图像不同种类的几何特征如：大小、灰度、方向、形状等，图像矩广泛应用于模式识别、目标分类、目标识别与防伪估计、图像编码与重构等领域。.
严格来讲矩是概率与统计中的一个概念，是随机变量的一种数字特征。设 x 为随机变量，C为常数，则量E[(x−c)^k]称为X关于C点的k阶矩。比较重要的两种情况如下：

一阶原点矩就是期望，一阶中心矩μ_1=0，二阶中心矩μ_2就是X的方差Var(X)。在统计学上，高于4阶的矩极少使用，μ_3可以去衡量分布是否有偏，μ_4可以衡量分布（密度）在均值拘谨的陡峭程度。

3、针对一幅图像，我们把像素的坐标看成是一个二维随机变量(X, Y)，那么一副灰度图可以用二维灰度图密度函数来表示，因此可以用矩来描述灰度图像的特征。 图像可以看成是一个平板的物体，其一阶矩和零阶矩就可以拿来计算某个形状的重心，而二阶矩就可以拿来计算形状的方向。

其中M00即零阶矩，M20和M02为二阶矩，接下来计算物体形状的方向

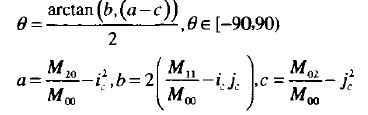
4、不变矩(Invariant Moments)是一种高度浓缩的图像特征，具有平移、灰度、尺度、旋转不变性，由M.K.Hu在1961年首先提出，1979年M.R.Teague根据正交多项式理论提出了Zernike矩。不变矩的物理含义：

如果把图像看成是一块质量密度不均匀的薄板，其图像的灰度分布函数f(x,y)就是薄板的密度分布函数，则其各阶矩有着不同的含义，如零阶矩表示它的总质量；一阶矩表示它的质心；二阶矩又叫惯性矩，表示图像的大小和方向。事实上，如果仅考虑阶次为2的矩集，则原始图像等同于一个具有确定的大小、方向和离心率，以图像质心为中心且具有恒定辐射率的椭圆。由三阶矩以下矩构成的七个矩不变量具有平移、旋转和尺度不变性等等。当密度分布函数发生改变时，图像的实质没有改变，仍然可以看做一个薄板，只是密度分布有所改变。虽然此时各阶矩的值可能发生变化，但由各阶矩计算出的不变矩仍具有平移、旋转和尺度不变性。通过这个思想，可对图像进行简化处理，保留最能反映目标特性的信息，再用简化后的图像计算不变矩特征，可减少计算量。

（研究表明，只有基于二阶矩的不变矩对二维物体的描述才是真正的与旋转、平移和尺度无关的。较高阶的矩对于成像过程中的误差，微小的变形等因素非常敏感，所以相应的不变矩基本上不能用于有效的物体识别。即使是基于二阶矩的不变矩也只能用来识别外形相差特别大的物理，否则他们的不变矩会因为很相似而不能识别。）

在OpenCV中，还可以很方便的得到Hu不变距，Hu不变矩在图像旋转、缩放、平移等操作后，仍能保持矩的不变性，所以有时候用Hu不变距更能识别图像的特征。

不变矩的应用过程一般包括：
1）选择合适的不变矩类型；
2）选择分类器（如神经网络、最短距离等）；
3）如果是神经网络分类器，则需要计算学习样例的不变矩去训练神经网络；
4）计算待识别对象的不变矩，输入神经网络就可得到待识别对象的类型，或者计算待识别对象不变矩与类别对象不变矩之间的距离，选择最短距离的类别作为待识别对象的类别。

可以看出，不变矩作用主要目的是描述事物（图像）的特征。人眼识别图像的特征往往又表现为“求和”的形式，因此不变矩是对图像素进行了积分操作。不变矩能够描述图像整体特征就是因为它具有平移不变形、比例不变性和旋转不变性等性质。然而，另一方面图像的各阶不变矩究竟代表的什么特征很难进行直观的物理解释。

二、相关算子

1、moments()函数

特征矩的知识在概率论和数理统计中有介绍，空间矩的方法在图像应用中比较广泛，包括零阶矩求面积、一阶矩确定重心、二阶矩确定主方向、二阶矩和三阶矩可以推导出七个不变矩-Hu不变矩，不变矩具有旋转，平移、缩放等不变性，因此在工业应用和模式识别中得到广泛的应用。

该函数计算多边形或栅格化形状（一个矢量形状或光栅形状）的最高达三阶所有矩。结果在结构cv::Moments 中返回

Moments cv::moments( InputArray array, // 光栅图像(单通道、8位或浮点二维数组)或二维点(点或点2f)的数组(1×N或N×1) bool binaryImage = false // binaryImage用来指示输出图像是否为一幅二值图像，如果是二值图像，则图像中所有非0像素看作为1进行计算。 ) 

结构 Moments 成员数据：

cv::Moments::Moments ( // 空间矩(10个) double m00,double m10,double m01,double m20,double m11,double m02,double m30,double m21,double m12,double m03 // 中心矩（7个） double mu20, double mu11, double mu02, double mu30, double mu21 , double mu12,double mu03 // 中心归一化矩（）  double nu20, double nu11, double nu02, double nu30, double nu21, double nu12,double nu03; ) 

1）空间矩 Moments::mji 的计算公式：

对于01二值化的图像，m00即为轮廓的面积
2）中心距 Moments::muji 计算公式：

其中：(x¯,y¯)为轮廓质心：

3）归一化的中心矩Moments::nuji计算公式为：

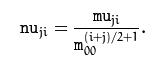
注意：
mu00=m00, nu00=1nu10=mu10=mu01=mu10=0 , 因此不存储值。
轮廓的矩是用同样的方法定义的，但是使用格林公式计算(参见http://en.wikipedia.org/wiki/Green_theorem)。因此，由于栅格分辨率的限制，计算轮廓的矩与计算相同栅格化轮廓的矩略有不同。
由于轮廓的矩是用格林公式计算的，对于具有自交点的轮廓，你可能会得到看似奇怪的结果，例如蝴蝶形轮廓的面积(m00)。

2、示例：（绘制轮廓及其质心，计算轮廓面积和长度）

使用到的算子：
1）绘制带箭头的直线(arrowedLine)
2）OpenCV—椭圆拟合fitEllipse

#include <opencv2/opencv.hpp> using namespace cv; using namespace std; int thresh=50; RNG rng(12345); int main() { 
    // 1、 读取图片 //Mat src