CaiT

paper:https://arxiv.org/abs/2103.17239
浅谈 CaiT
Hi guy!我们又见面了,这次来解析一篇来自 FaceBook AI 的一篇视觉 Transformer 的相关工作 CaiT

Transformer 在视觉领域可谓风生水起,各大视觉相关榜单都被刷爆了,自从 Google 的 ViT: An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale 开始,很多研究者展开了基于 ViT 的改进工作,比较著名的是 DeiT、Swin Transformer、PVT 等视觉 Transformer 改进,以及一些新架构 MLP-Mixer、ResMLP、gMLP 等。毫无疑问,今年是视觉 Transformer 大爆炸的一年,这在 CVPR、ICCV 等视觉相关顶会可见一斑。
ViT 尽管取得了很高的精度,但这离不开大规模数据训练(JFT-300M),而且这样的数据集不开源,很多工作致力于解决 ViT 的数据问题和计算开销问题。数据问题是指 ViT 这样的视觉 Transformer 缺少一定的归纳偏置,需要更多的数据(相比 ConvNet 网络)来训练,否则很容易在小数据集上过拟合,参数量越大的模型越明显。计算开销问题是指 ViT 中的 MHSA 计算量与 Token 数平方相关(O(n2)),尽管提升 Token 数可以获得更好的表征从而得到更高的精度(这也是最简单直接的办法),但是其计算复杂度随着 Token 数增加呈二次方发展,这将会给模型带来庞大的计算量。
针对上述问题后续很多工作给出了改进,比如 DeiT 在蒸馏中引入 distillation token,LV-ViT 通过 token labeling 技巧辅助训练, 以及最近的 BEiT、MAE、MaskFeat 等自监督训练,这些都很好解决了视觉 Transformer 的数据问题,它们旨在让 ViT 仅在 ImageNet-1K 下就能获得具有竞争力的性能。而在计算量问题上,有诸如 Swin Transformer、CvT 等通过改进 MHSA(Multi-Head Self Attention)来降低计算量,也有 PVT/PVT v2 这样通过将 ViT 的直筒式结构改成金字塔结构以此来降低计算量。
相比上述工作,CaiT 则是思考如何加深网络
根据以前的经验,增加模型的深度可以使得网络学习更复杂的表征,比如 ResNet 从18 层到 152 层,随着层数的增加其精度逐渐提高
| Model | ACC@1 | ACC@5 |
|---|---|---|
| ResNet-18 | 69.758 | 89.078 |
| ResNet-34 | 73.314 | 91.420 |
| ResNet-50 | 76.130 | 92.862 |
| ResNet-101 | 77.374 | 93.546 |
| ResNet-152 | 78.312 | 94.046 |
但是在 Transformer 中,当我们扩展架构时,模型变得越来越难训练,其中深度是不稳定的主要来源之一,例如 DeiT-S 在不调整超参数情况下不能正确收敛到 18 层以上,尽管结合一些调参技巧如线性调整 drop rate,DeiT-S 依然在36层达到饱和(实验均在 ImageNet 1K 下进行)
| Depth | Acc@1 - dr=0.05 | Acc@1 - dr= linear |
|---|---|---|
| DeiT-S12 | 79.9 | 79.9 |
| DeiT-S18 | 80.1 | 80.7 |
| DeiT-S24 | 78.9 ↓ | 81.0 |
| DeiT-S36 | 78.9 ↓ | 81.9 |
| DeiT-S48 | - | 80.7 ↓ |
为了解决深度问题,CaiT 提出了两个改进,一个是 LayerScale,一个是 Class-Attention
LayerScale 在每个残差块的输出上添加一个可学习的对角矩阵,该矩阵被初始化为接近0。在每个残差块之后添加这个简单的层可以提高训练的动态性,使我们能够训练更深层次的大容量 Transformer,如下所示
x l ′ = x l + d i a g ( λ 1 , . . . , λ d ) × S A ( N o r m ( x l ) ) x_{l}^{'}=x_l+diag(\lambda_1,...,\lambda _d)\times SA(Norm(x_l)) xl′=xl+diag(λ1,...,λd)×SA(Norm(xl))
x l + 1 = x l ′ + d i a g ( λ 1 ′ , . . . , λ d ′ ) × F F N ( N o r m ( x l ′ ) ) x_{l+1}=x_{l}^{'}+diag(\lambda_{1}^{'},...,\lambda_{d}^{'})\times FFN(Norm(x_{l}^{'})) xl+1=xl′+diag(λ1′,...,λd′)×FFN(Norm(xl′))

Class-Attention 是一个类似于 Encode/Decode 的结构,和 Self-Attention 不同,Class-Attention 更注重从处理过的 patches token 中提取信息,相比 SA 主要是 Q(query)的自变量 z 变成 xclass,而 K(keys)、V(value)则保持不变,如下所示
Q = W q x c l a s s + b q Q=W_q x_{class}+b_q Q=Wqxclass+bq
K = W k z + b k K=W_kz+b_k K=Wkz+bk
V = W v z + b v V=W_vz+b_v V=Wvz+bv
其中
z = [ x c l a s s , x p a t c h e s ] z=[x_{class},x_{patches}] z=[xclass,xpatches]
流程解析
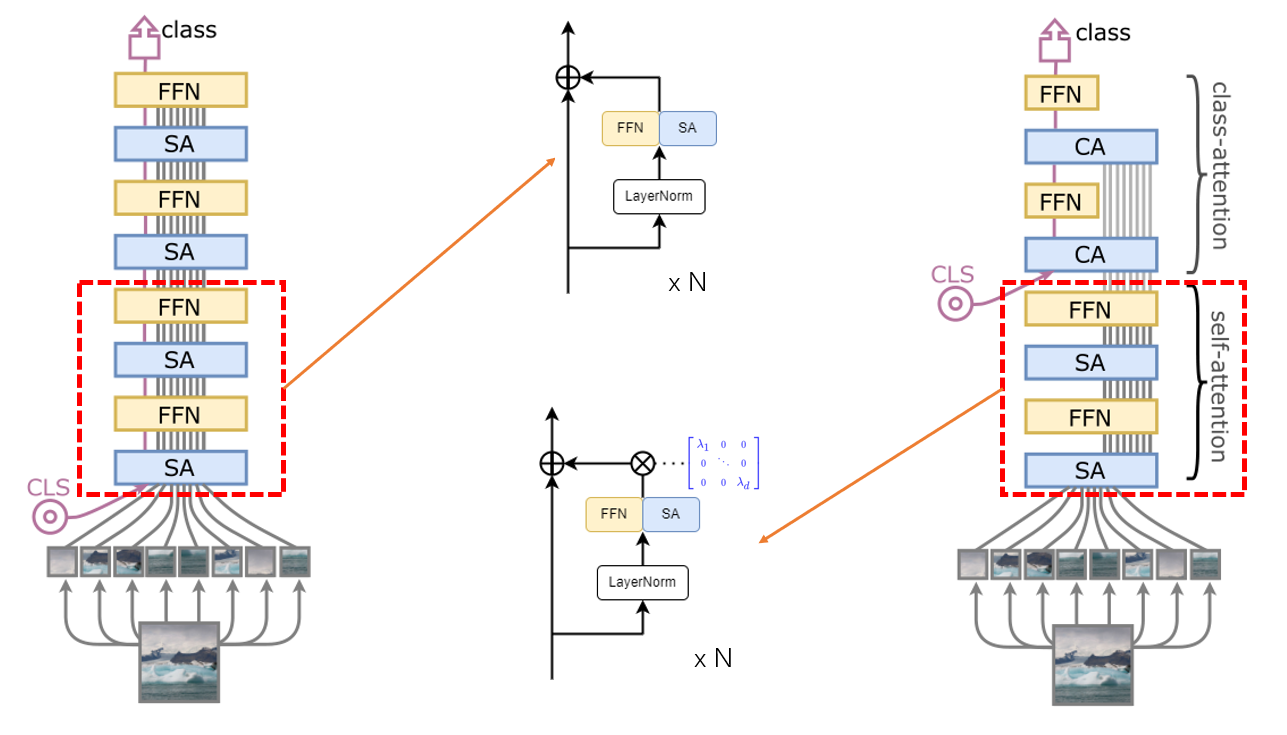
我们先看一下论文给出的结构图,如下所示

左边是 ViT 网络结构,CLS(classes token)与 Patch Embedding 一起被送进网络,最后输出 CLS 做分类
右边则是 CaiT 网络结构,相对于左边的 ViT 结构而言,最直观的变化是 CLA 被放入网络更深的层。
下面我们详细过一遍 CaiT 的流程,CaiT 流程可以分为三个部分,如下图所示

首先是 patch embedding 操作,将输入划分为不同的 patches。Patch Embedding 是视觉 Transformer 常见的操作,这里不做过多的解释,相关代码如下所示
class PatchEmbed(nn.Layer): """ 2D Image to Patch Embedding """ def __init__(self, img_size=224, patch_size=16, in_chans=3, embed_dim=768, norm_layer=None, flatten=True): super().__init__() img_size = (img_size, img_size) patch_size = (patch_size, patch_size) self.img_size = img_size self.patch_size = patch_size self.grid_size = (img_size[0] // patch_size[0], img_size[1] // patch_size[1]) self.num_patches = self.grid_size[0] * self.grid_size[1] self.flatten = flatten self.proj = nn.Conv2D(in_chans, embed_dim, kernel_size=patch_size, stride=patch_size) self.norm = norm_layer(embed_dim) if norm_layer else Identity() def forward(self, x): B, C, H, W = x.shape assert H == self.img_size[0] and W == self.img_size[1], \ f"Input image size ({
H}*{
W}) doesn't match model ({
self.img_size[0]}*{
self.img_size[1]})." x = self.proj(x) if self.flatten: x = x.flatten(2).transpose((0, 2, 1)) # BCHW -> BNC x = self.norm(x) return x 接下来是 Self-Attention 操作,和 ViT 不一样的是,CaiT 提出了 LayerScale,在每个残差块的输出乘上一个对角矩阵,如下图所示(详细公式在上面)
其中 λ1、λ2、…、λd 是对角线上的素,是可学习参数
添加 LayerScale 不仅不会改变结构的表现能力,而且可以使得更深的模型收敛,如下图所示。作者对 LayerScale 的 λ 初始化进行了研究,发现对 λi 进行常量初始化可以取得更好的结果

λi = 0 表示 0 初始化,λi = u[0, 2ε] 表示均匀初始化,λi = ε 表示常量(略大于 0)初始化
相关代码如下所示
class LayerScaleBlock(nn.Layer): def __init__(self, dim, num_heads, mlp_ratio=4., qkv_bias=False, drop=0., attn_drop=0., drop_path=0., act_layer=nn.GELU, norm_layer=nn.LayerNorm, attn_block=TalkingHeadAttn, mlp_block=Mlp, init_values=1e-5): super().__init__() self.norm1 = norm_layer(dim) self.attn = attn_block(dim, num_heads=num_heads, qkv_bias=qkv_bias, attn_drop=attn_drop, proj_drop=drop) self.drop_path = DropPath(drop_path) if drop_path > 0. else Identity() self.norm2 = norm_layer(dim) mlp_hidden_dim = int(dim * mlp_ratio) self.mlp = mlp_block(in_features=dim, hidden_features=mlp_hidden_dim, act_layer=act_layer, drop=drop) self.gamma_1 = paddle.create_parameter( shape=[dim], dtype='float32', default_initializer=nn.initializer.Constant(init_values)) self.gamma_2 = paddle.create_parameter( shape=[dim], dtype='float32', default_initializer=nn.initializer.Constant(init_values)) def forward(self, x): x = x + self.drop_path(self.gamma_1 * self.attn(self.norm1(x))) # LayerScale x = x + self.drop_path(self.gamma_2 * self.mlp(self.norm2(x))) # LayerScale return x 最后则是 Class-Attention(CA)模块,CA 层的作用是利用 CLS 从处理过的 patches embeding 中提取提取信息,在讨论 CA 之前,我们先搞明白为什么 CLS 要在网络后期 CA 部分插入
作者认为是 clas token 在网络前期使用的任务的矛盾,一方面它要用于最后概括总信息的类别预测,一方面又要在每层辅助全图特征的更新,这两个任务加在一起会让 clas token 的优化变得迷茫,实验结果也很好证明了 CLS 放在后面有助于性能的提高

CA 部分的计算公式如下所示
Q = W q x c l a s s + b q , K = W k z + b k , V = W v z + b v Q=W_q x_{class}+b_q,K=W_kz+b_k,V=W_vz+b_v Q=Wqxclass+bq,K=Wkz+bk,V=Wvz+bv
A = S o f t m a x ( Q ⋅ K T d / h ) A = Softmax(\frac{Q\cdot K^T}{\sqrt{d/h}}) A=Softmax(d/hQ⋅KT)
o u t C A = W o A V + b o out_{CA}=W_oAV+b_o outCA=WoAV+bo
其中
z = [ x c l a s s , x p a t c h e s ] , z=[x_{class},x_{patches}], z=[xclass,xpatches],
CA 比 SA 具有更小的计算开销,因为它计算 class token 和处理过的 patches embeding 之间的关注度,换句话说,在额外的 CaiT 层(指CA)中,计算复杂度为patches 数的线性复杂度(SA:O(n2) --> CA:O(n))。
相关代码如下所示
class ClassAttn(nn.Layer): def __init__(self, dim, num_heads=8, qkv_bias=False, attn_drop=0., proj_drop=0.): super().__init__() self.num_heads = num_heads head_dim = dim // num_heads self.scale = head_dim-0.5 self.q = nn.Linear(dim, dim, bias_attr=qkv_bias) self.k = nn.Linear(dim, dim, bias_attr=qkv_bias) self.v = nn.Linear(dim, dim, bias_attr=qkv_bias) self.attn_drop = nn.Dropout(attn_drop) self.proj = nn.Linear(dim, dim) self.proj_drop = nn.Dropout(proj_drop) def forward(self, x): B, N, C = x.shape q = self.q(x[:, 0]).unsqueeze(1).reshape([B, 1, self.num_heads, C // self.num_heads]).transpose([0, 2, 1, 3]) k = self.k(x).reshape([B, N, self.num_heads, C // self.num_heads]).transpose([0, 2, 1, 3]) q = q * self.scale v = self.v(x).reshape([B, N, self.num_heads, C // self.num_heads]).transpose([0, 2, 1, 3]) attn = (q @ k.transpose([0, 1, 3, 2])) attn = F.softmax(attn, axis=-1) attn = self.attn_drop(attn) x_cls = (attn @ v).transpose([0, 2, 1, 3]).reshape([B, 1, C]) x_cls = self.proj(x_cls) x_cls = self.proj_drop(x_cls) return x_cls CaiT 仅在 ImageNet 数据集上就取得了不俗的结果,性能优于 ViT、DeiT,具体性能如下所示

PASSL 已支持 CaiT
PASSL 包含 SimCLR、MoCo v1/v2、BYOL、CLIP 等基于对比学习的图像自监督算法以及 Vision Transformer、Swin Transformer、BEiT、CvT、T2T-ViT、MLP-Mixer 等视觉 Transformer 及相关算法,欢迎 star ~
PASSL github:https://github.com/PaddlePaddle/PASSL
CaiT 性能
The results are evaluated on ImageNet2012 validation set
| Arch | Weight | Top-1 Acc | Top-5 Acc | Crop ratio | # Params |
|---|---|---|---|---|---|
| cait_s24_224 | pretrain 1k | 83.45 | 96.57 | 1.0 | 46.8M |
| cait_xs24_384 | pretrain 1k | 84.06 | 96.89 | 1.0 | 26.5M |
| cait_s24_384 | pretrain 1k | 85.05 | 97.34 | 1.0 | 46.8M |
| cait_s36_384 | pretrain 1k | 85.45 | 97.48 | 1.0 | 68.1M |
| cait_m36_384 | pretrain 1k | 86.06 | 97.73 | 1.0 | 270.7M |
| cait_m48_448 | pretrain 1k | 86.49 | 97.75 | 1.0 | 355.8M |
更详细内容可见:https://github.com/PaddlePaddle/PASSL/tree/main/configs/cait
!git clone https://github.com/PaddlePaddle/PASSL.git # 克隆 PASSL,连不上多试几次 !pip install ftfy # 安装依赖 !pip install regex # 安装依赖 %cd PASSL import paddle from passl.modeling.backbones import build_backbone from passl.modeling.heads import build_head from passl.utils.config import get_config class Model(paddle.nn.Layer): def __init__(self, cfg_file): super().__init__() cfg = get_config(cfg_file) self.backbone = build_backbone(cfg.model.architecture) self.head = build_head(cfg.model.head) def forward(self, x): x = self.backbone(x) x = self.head(x) return x cfg_file = 'configs/cait/cait_s24_224.yaml' # CaiT 配置文件 m = Model(cfg_file) # 模型组网 x = paddle.randn([2, 3, 224, 224]) # test out = m(x) loss = out.sum() loss.backward() print('Single iteration completed successfully') 总结
作为来自 FAI 的工作,CaiT 具有一定的 insight。目前在视觉 Transformer 中很多人提高模型精度是通过减小 patch size 尽可能将图像分成更多的patches,这无疑会给模型带来二次方增长的计算量,CaiT 证明了我们其实还可以突破层数的瓶颈,构造模型的深窄结构来进一步增强模型的表征能力。
今天的文章 【视觉 Transformer】超详细解读 CaiT 模型分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/bian-cheng-ji-chu/96544.html