什么是高等数学？

↑↑↑ 关注“图灵课堂”，积累新知·学会思考

数学是从具体到抽象，再抽象的过程，从自然数到集合，从集合到群，从群到拓扑，从拓扑到流形。

小初高阶段我们学习的数学为什么到了大学以后要叫“高等”数学呢？初入大学的你知道什么是高等数学吗？你了解高等数学吗？今天小编就给大家科普一下什么是高等数学。

一、什么是高等数学？

高等数学是一门涵盖了多种数学分支的课程，由微积分学，较深入的代数学、几何学以及它们之间的交叉内容所形成的一门基础学科。主要内容包括：数列、极限、微积分、空间解析几何与线性代数、级数、常微分方程。

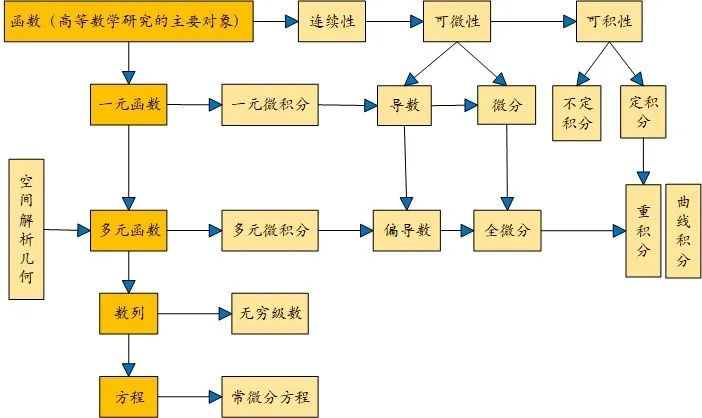
二、为什么称之为“高等”数学？

小初高阶段我们所学的数学称为“初等”数学，重在能灵活运用定理、公式解决一些实际问题。高等数学是大学阶段理工科专业必修的一门重要基础课程，重在掌握定理、公式的推理及应用，也就是说，高等数学的“高等”主要体现在其使用的是一种新的逻辑，从逻辑上要求非常严格。高等数学的产生和发展是从常量数学过渡到变量数学，从命题逻辑过渡到谓词逻辑的过程，关注的是一种全新的模式——极限，使用的刻画方法也只有用谓词逻辑才能表达清楚。

三、高等数学回答了什么问题？

数学分析：主要包括微积分和级数理论。微积分是高等数学的基础，应用范围非常广，基本上涉及到函数的领域都需要微积分的知识。级数中，傅立叶级数和傅立叶变换主要应用在信号分析领域，包括滤波、数据压缩、电力系统的监控等，电子产品的制造离不开它。

实变函数（实分析）：数学分析的加强版之一。主要应用于经济学等注重数据分析的领域。

复变函数（复分析）：数学分析加强版之二。应用很广的一门学科，在航空力学、流体力学、固体力学、信息工程、电气工程等领域都有广泛的应用，所以工科学生都要学这门课的。

高等代数，主要包括线形代数和多项式理论。线形代数可以说是目前应用很广泛的数学分支，数据结构、程序算法、机械设计、电子电路、电子信号、自动控制、经济分析、管理科学、医学、会计等都需要用到线形代数的知识，是目前经管、理工、计算机专业学生的必修课程。

高等几何：包括空间解析几何、射影几何、球面几何等，主要应用在建筑设计、工程制图方面。

分析学、高等代数、高等几何是近代数学的三大支柱。

微分方程：包括常微分方程和偏微分方程，重要工具之一。流体力学、超导技术、量子力学、数理金融、材料科学、模式识别、信号(图像)处理、工业控制、输配电、遥感测控、传染病分析、天气预报等领域都需要它。

泛函分析：主要研究无限维空间上的函数。因为比较抽象，在技术上的直接应用不多，一般应用于连续介质力学、量子物理、计算数学、控制论、最优化理论等理论。

近世代数（抽象代数）：主要研究各种公理化抽象代数系统的。技术上没有应用，物理上用得比较多，尤其是其中的群论。

拓扑学：研究集合在连续变换下的不变性。在自然科学中应用较多，如物理学的液晶结构缺陷的分类、化学的分子拓扑构形、生物学的DNA的环绕和拓扑异构酶等，此外在经济学中也有很重要的应用。

泛函分析、近世代数、拓扑学是现代数学三大热门分支。

非欧几何：主要应用在物理上，最著名的是相对论。

数论：曾经被认为是数学家的游戏、唯一不会有什么应用价值的分支。著名的哥德巴赫猜想就是数论里的。现在随着网络加密技术的发展，数论也找到了自己用武之地——密码学。

四、课程特点

作为一门基础科学，高等数学有其固有的特点，这就是高度的抽象性、严密的逻辑性和广泛的应用性。抽象性和应用性是数学最基本、最显著的特点，有了高度抽象和统一，我们才能深入地揭示其本质规律，使之得到更广泛的应用。严密的逻辑性是指在数学理论的归纳和整理中，无论是概念和表述，还是判断和推理，都要运用逻辑的规则，遵循思维的规律。所以说，数学也是一种思想方法，学习数学的过程就是思维训练的过程。人类社会的进步，与数学这门科学的广泛应用是分不开的。尤其是到了现代，电子计算机的出现和普及使得数学的应用领域更加拓宽，现代数学正成为科技发展的强大动力，同时也广泛和深入地渗透到了社会科学领域。

到目前为止，数学的所有一级分支都已经找到了应用领域，从自然科学、社会科学、工程技术到信息技术，数学的影响无处不在。如果没有高等数学在二十世纪的发展，我们平时所玩的电脑、上的网络、听的mp3、用的手机都不可能存在。当然，一般的普通大众是没必要了结这些艰深抽象的东西，但是它们的存在和发展却是必需的，总要有一些人去研究这些。

因此，深入掌握高等数学的精髓对于个人发展具有不可估量的价值，它不仅锻炼了我们的逻辑思维能力，提升了问题解决能力，为职业生涯铺设了坚实的基石，更在个人成长的道路上，培养了我们面对复杂挑战时的耐心和毅力，成为我们终身学习和适应快速变化社会的宝贵财富。

今天的文章什么是高等数学？分享到此就结束了，感谢您的阅读。

什么是高等数学？

相关推荐