1. 首页首页
  2. 编程基础编程基础

（四）流体动力学（动量守恒和能量守恒）

编程基础 • • 阅读 11

（四）流体动力学（动量守恒和能量守恒）本文详细介绍了理想流体的动量守恒与能量守恒 重点讨论了理想流体的伯努利方程 包括沿流线与总流的伯努利方程 并解释了其物理意义和适用条件

目录

（一）理性流体运动微分方程（动量守恒）

（二）理想流体沿流线伯努利方程（能量守恒）

（三）理想流体沿流线伯努利方程的意义

（四）理想流体总流伯努利方程

（五）实际流体总流的伯努利方程

（六）伯努利方程的推广

（七）存在机械能输出和输入时总的伯努利方程

（一）理性流体运动微分方程（动量守恒）

理想流体微分方程也叫做欧拉运动微分方程。是牛顿第二定律在理想流体中的应用。

表达式为：

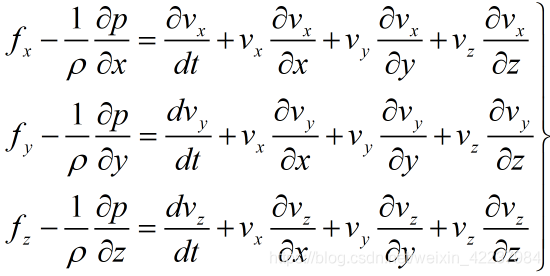
物理意义：理想流体微分方程表达了作用在单位质量流体上的力与流体运动加速度之间的关系，是流体动力学的基本方程，对于不可压缩和可压缩的流体均适用，也适用于所有的理想流体的运动。

（二）理想流体沿流线伯努利方程（能量守恒）

理想流体沿流线的伯努利方程如下所示：

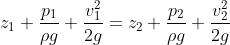
z_{1}+\frac{p_{1}}{\rho g}+\frac{v_{1}^{2}}{2g}=z_{2}+\frac{p_{2}}{\rho g}+\frac{v_{2}^{2}}{2g}

适用范围

  • 理想不可压缩流体
  • 质量力只有重力
  • 稳定流动
  • 对于有旋流动，仅适用于同一条流线；对于无旋流动，整个流场都适用。

（三）理想流体沿流线伯努利方程的意义

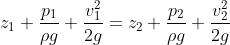
z_{1}+\frac{p_{1}}{\rho g}+\frac{v_{1}^{2}}{2g}=z_{2}+\frac{p_{2}}{\rho g}+\frac{v_{2}^{2}}{2g}

几何意义

  • z——称为位置水头；
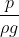  • \frac{p}{\rho g}——测压管高度，速度水头；
今天的文章 （四）流体动力学（动量守恒和能量守恒）分享到此就结束了，感谢您的阅读。
编程小号
上一篇 2025-01-01 12:30
下一篇 2025-01-01 12:27

相关推荐

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请发送邮件至 举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/bian-cheng-ji-chu/98754.html