百科上的定义:
极限是微积分中的基础概念,它指的是变量在一定的变化过程中,从总的来说逐渐稳定的这样一种变化趋势以及所趋向的值(极限值)。极限的概念最终由柯西和魏尔斯特拉斯等人严格阐述。在现代的数学分析教科书中,几乎所有基本概念(连续、微分、积分)都是建立在极限概念的基础之上。
极限符号:
取极限: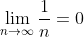 表示当n无限趋近于正无穷时。
表示当n无限趋近于正无穷时。 趋近于0.
趋近于0.
数列极限:
定义:
- 数列是按照正整数顺序排列的无穷多个数:
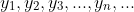
简记为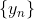 ,其中数列第n项,
,其中数列第n项, 为该数列的通项。
为该数列的通项。
- 数列其实是一种特殊的函数:

而我们要研究的是,当 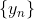 的项数n无限增大时,
的项数n无限增大时,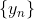 的变化趋势?
的变化趋势?
给定一个数列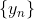 ,如果当n无限增大时,其通项
,如果当n无限增大时,其通项 无限的趋近于某个常数A,则称数列
无限的趋近于某个常数A,则称数列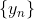 以A为极限,记作:
以A为极限,记作: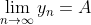 或
或 .
.
当数列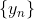 以A为极限时,称数列
以A为极限时,称数列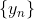 收敛于A,此时也称数列
收敛于A,此时也称数列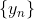 收敛于A,如果
收敛于A,如果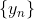 不收敛于任何常数,则称数列
不收敛于任何常数,则称数列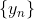 是发散数列。
是发散数列。
例子: 收敛于0,
收敛于0, 收敛于1.
收敛于1.
 没有极限,数列
没有极限,数列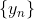 是发散的。
是发散的。
函数极限:
对于函数的极限,根据自变量的变化过程可以分为两种情形:
- 自变量趋于无穷大的极限;
- 自变量趋于定点的极限;
(一)自变量趋于无穷大的极限:
 表示x沿着x轴正半轴趋于正无穷;
表示x沿着x轴正半轴趋于正无穷; 表示x沿着x轴负半轴趋于负无穷;
表示x沿着x轴负半轴趋于负无穷; 表示x沿着x轴任意方向趋于无穷;
表示x沿着x轴任意方向趋于无穷;
定义:
- 设函数
 在区间
在区间 上有定义,A为常数,如果当
上有定义,A为常数,如果当 时,函数值
时,函数值  无限趋近于常数A,则称当
无限趋近于常数A,则称当 时,
时, 以A为极限。记作
以A为极限。记作 或
或 ;
; - 设函数
 在区间
在区间![(-\infty,a]](/uploads/202410/10/20074b3421525411.webp) 上有定义,A为常数,如果当
上有定义,A为常数,如果当 时,函数值
时,函数值  无限趋近于常数A,则称当
无限趋近于常数A,则称当 时,
时, 以A为极限。记作
以A为极限。记作 或
或 ;
; - 设函数
 在区间
在区间 上有定义,A为常数,如果当
上有定义,A为常数,如果当 时,函数值
时,函数值  无限趋近于常数A,则称当
无限趋近于常数A,则称当 时,
时, 以A为极限。记作
以A为极限。记作 或
或 ;(应当注意,
;(应当注意, 包含+
包含+ 和-
和- 两种情况讨论.如
两种情况讨论.如  )
)
由如上定义可知: 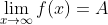 存在的条件 为:
存在的条件 为: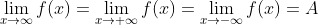
(二)自变量趋于定点的极限:
 表示
表示 从
从 的左侧无限趋近于
的左侧无限趋近于 ,此时
,此时 ;
; 表示
表示 从
从 的右侧无限趋近于
的右侧无限趋近于 ,此时
,此时 ;
; 表示
表示 从
从 的左右两侧无限趋近于
的左右两侧无限趋近于 .
.
注意:
- x是一个变化的量,是动点,
 是一个常数.
是一个常数. - 上述的三个变化过程中,
 .
.
例题:
1.讨论当 时,y = 3x-1的变化趋势:
时,y = 3x-1的变化趋势:
解法很简单,由于是一个一次函数,可以直接得出,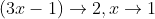
2.讨论当 时,
时,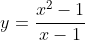 的变化趋势:
的变化趋势:
解法:由于 可以得到
可以得到  ,但
,但 ,所以
,所以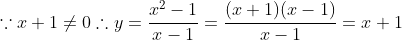 .
.
故 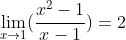 .
.
定义:
- 设函数
 在x的邻域有定义(无所谓x是否有
在x的邻域有定义(无所谓x是否有 的定义),A为常数,如果当
的定义),A为常数,如果当 时,函数值
时,函数值  无限趋近于常数A,则称当
无限趋近于常数A,则称当 时,
时, 以A为极限。记作
以A为极限。记作 或
或 ;
;
左、右极限:
- A为常数,如果当
 时,函数值
时,函数值  无限趋近于常数A,则称当
无限趋近于常数A,则称当 时,
时, 以A为左极限。记作
以A为左极限。记作 或
或 ;
; - A为常数,如果当
 时,函数值
时,函数值  无限趋近于常数A,则称当
无限趋近于常数A,则称当 时,
时, 以A为右极限。记作
以A为右极限。记作 或
或 ;
;
定理: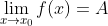 存在的必要条件是:
存在的必要条件是: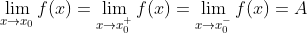


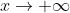 表示x沿着x轴正半轴趋于正无穷;
表示x沿着x轴正半轴趋于正无穷;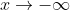 表示x沿着x轴负半轴趋于负无穷;
表示x沿着x轴负半轴趋于负无穷;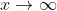 表示x沿着x轴任意方向趋于无穷;
表示x沿着x轴任意方向趋于无穷; 在区间
在区间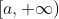 上有定义,A为常数,如果当
上有定义,A为常数,如果当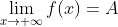 或
或 ;
;![(-\infty,a]](https://i-blog.csdnimg.cn/blog_migrate/2abed554c4f060624d4cd6e53267623d.gif) 上有定义,A为常数,如果当
上有定义,A为常数,如果当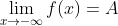 或
或 ;
;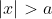 上有定义,A为常数,如果当
上有定义,A为常数,如果当 ;(应当注意,
;(应当注意, 包含+
包含+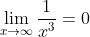 )
)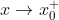 表示
表示 从
从 ;
; 表示
表示 ;
; 表示
表示 .
. 的定义),A为常数,如果当
的定义),A为常数,如果当 时,函数值
时,函数值  ;
; 时,函数值
时,函数值 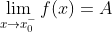 或
或 ;
; 时,函数值
时,函数值 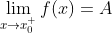 或
或 ;
;
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/bian-cheng-ji-chu/99444.html