使用最小二乘法求解回归方程并用matplotlib画出回归方程

前言
最小二乘法Least Square Method，做为分类回归算法的基础，有着悠久的历史（由马里·勒让德于1806年提出）。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。

导入包

import pandas as pd 
import matplotlib.pyplot as plt 
import numpy as np
from sklearn.linear_model import LinearRegression

根据预测目标，确定自变量和因变量：

data = pd.read_excel(
'D:\example_csv\data.xlsx')
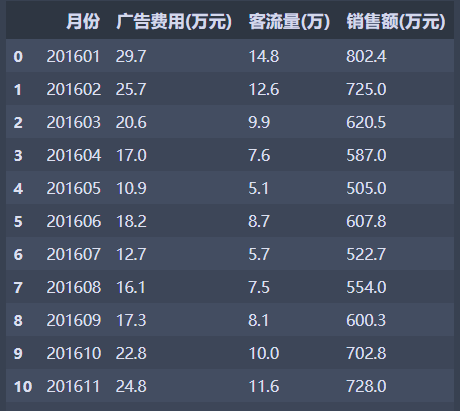
y = data['销售额(万元)'].values.reshape(-1, 1)#数据变为ndarray类型
x = data['广告费用(万元)'].values.reshape(-1, 1)

部分数据如下：

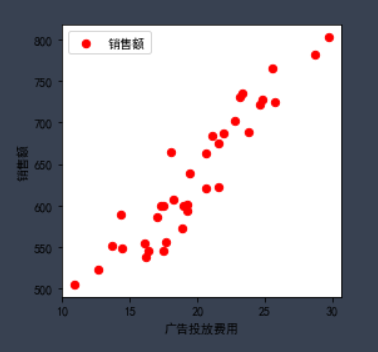
绘制散点图，确定回归模型类型：

plt.figure(figsize = (4,4)) #改变图示大小
plt.xlabel('广告投放费用')
plt.ylabel('销售额')
plt.scatter(x,y,marker = 'o',color = 'red',label = '销售额',s = 40)
#label作为图例
plt.legend(loc = 'best')
plt.show()

估计模型参数，建立线性回归模型：
Y = aX +b +e

lrModel = LinearRegression()
lrModel.fit(x,y) #使用自变量x，y训练模型

lrModel.coef_    #不要漏掉这两个下划线
lrModel.intercept_

就此可以得到一个简单的线性回归方程： 销售额 = 17.32*广告费用+291.90

对回归模型进行验证和预测：

lrModel.score(x,y)
y2 = pd.DataFrame({ 
   
    '广告费用(万元)':[10]
})#取第11个数据作为预测
lrModel.predict(y2)

结果越接近1，说明模型拟合效果越好

预测结果符合线性回归方程

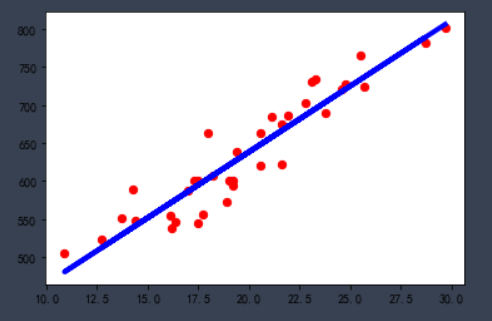
画出线性回归方程：

y2 = 17.32*x+291.90
plt.plot(x,y2,color = 'blue',linewidth = '4')
plt.scatter(x,y,marker = 'o',color = 'red',label = '销售额',s = 40)

今天的文章使用最小二乘法求解回归方程并用matplotlib画出回归方程分享到此就结束了，感谢您的阅读。