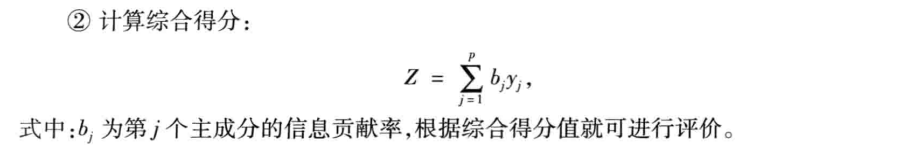数学建模之主成分分析（PCA）

本文参考的是司守奎，孙兆亮主编的数学建模算法与应用（第二版）

由于在学习数学建模的过程中，复现建模书上的题目代码有点小麻烦，因为我找不着书上的数据，因此得一个个手打，本来已经复现了好几个模型，结果因为机械硬盘坏了，里面的东西全没了，很是无语，因此决定在这里记录我的复现代码，主要是给自己看的，等到想用的时候就可以直接拿来用了。

主成分分析
可以用于降维，可以用于评价
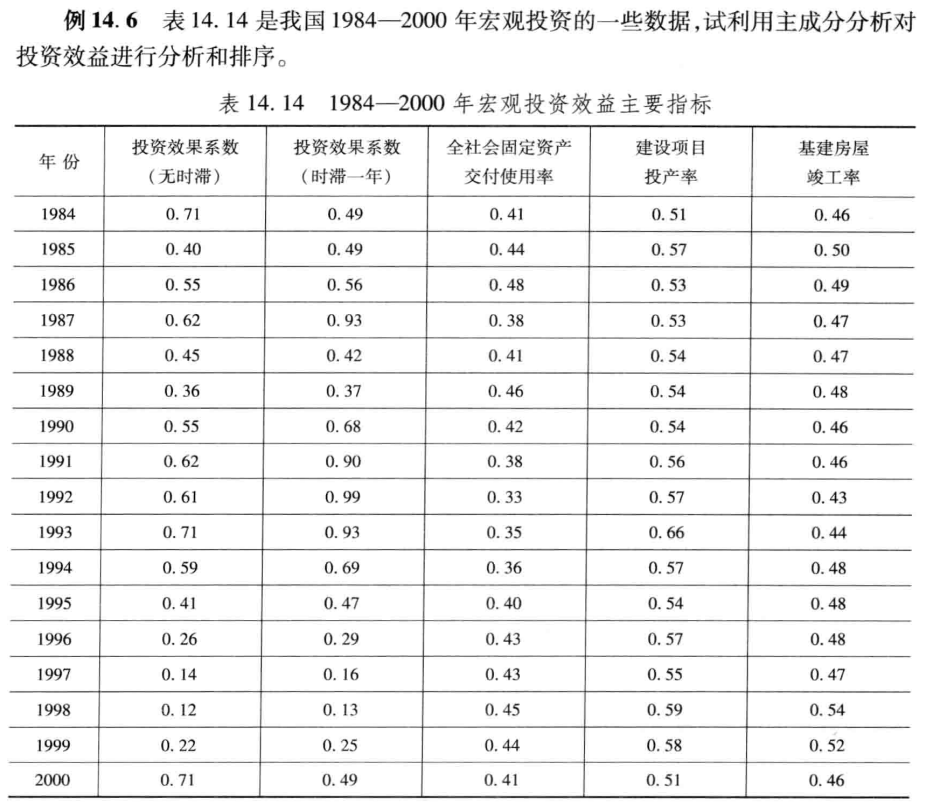
下面展示一道例题

这是书上的一道例题，需要使用主成分分析的方法进行评价。以前我一直以为PCA就是用来降维的，没想到还可用来评价，究其原因，我们都知道PCA降维会计算特征向量，其特征向量与原特征的积就是计算出的新特征，是一个具体的值，同时还会计算对于新特征的特征贡献率，可以理解为这个特征包含了原特征多少信息，一般到取到90%左右贡献率比较合适。
因此拥有90%左右特征贡献率的新特征就能够用于代替原特征，从而达到降维的效果。
那么如果很明确的知道原特征都是正向的评价，通过对新特征*特征贡献率进行求和，可以理解为对原来所有特征的综合评价，即可对这个事物进行评价了

首先，需要将数据标准化，即每个元素减去当前列的均值再除以当前列的标准差，注意这里的标准差是修正后的标准差，因此是1/n-1。

然后计算相关系数矩阵，这里使用的就是皮尔逊相关系数，对角线是自己和自己，因此相关系数为1

再计算特征值和特征向量

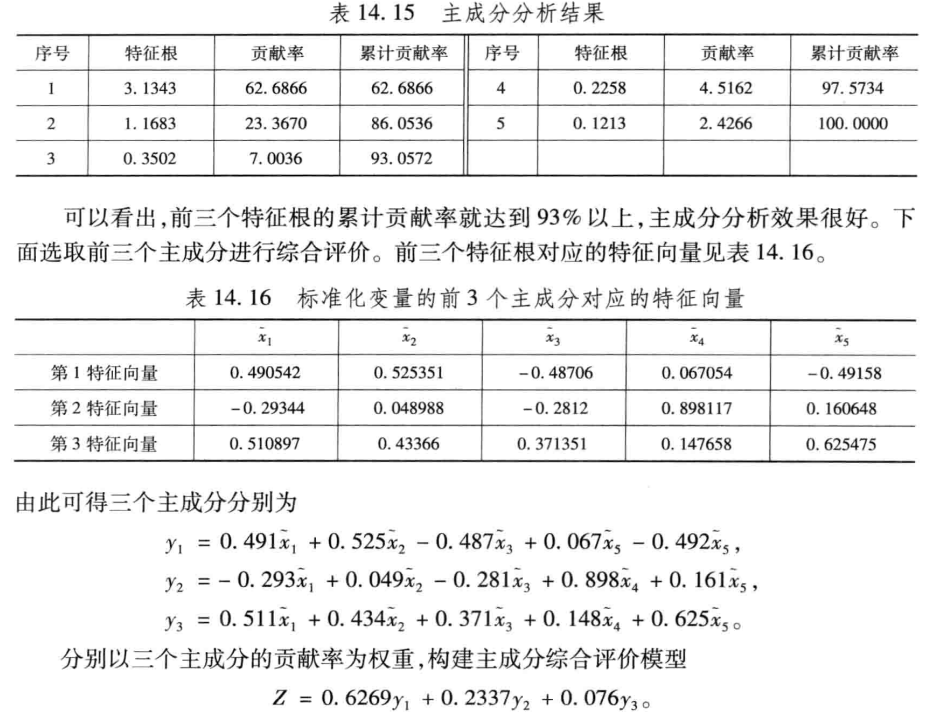
最后选择主成分个数（一般不超过5个）以及评分，首先需要计算特征值的信息贡献率，即这个特征包含了原有特征信息量的多少。因此得出的主成分能够代替原有的特征，从而达到降维的目的。
然后对于求主成分*对应信息贡献率再求和即可获得综合评分

matlab代码如下：

clc,clear
gj = [0.71 0.49 0.41 0.51 0.46
    0.40 0.49 0.44 0.57 0.50
    0.55 0.56 0.48 0.53 0.49
    0.62 0.93 0.38 0.53 0.47
    0.45 0.42 0.41 0.54 0.47
    0.36 0.37 0.46 0.54 0.48
    0.55 0.68 0.42 0.54 0.46
    0.62 0.90 0.38 0.56 0.46
    0.61 0.99 0.33 0.57 0.43
    0.71 0.93 0.35 0.66 0.44
    0.59 0.69 0.36 0.57 0.48
    0.41 0.47 0.40 0.54 0.48
    0.26 0.29 0.43 0.57 0.48
    0.14 0.16 0.43 0.55 0.47
    0.12 0.13 0.45 0.59 0.54
    0.22 0.25 0.44 0.58 0.52
    0.71 0.49 0.41 0.51 0.46];

gj = zscore(gj); % 数据标准化
r = corrcoef(gj); % 求相关系数矩阵
[x, y, z] = pcacov(r); % x的每列为r矩阵的特征向量即此新特征对应原各个特征的权值
% y为r的特征值 z为各个主成分即新特征的贡献率
f = repmat(sign(sum(x)), size(x,1), 1);% 构造与x同维数的元素为正负1的矩阵
x = x.*f %修改特征向量的正负号，每个特征向量*所有分量和的符号函数值,应该就是取新特征绝对值吧
num = 3;% 此题由于分析过取3个效果不错，对于新的分词这里需要进行相应改动
df = gj*x(:, [1:num]); % 计算各个主成分的得分
tf = df * z(1:num)/100;% 计算综合得分
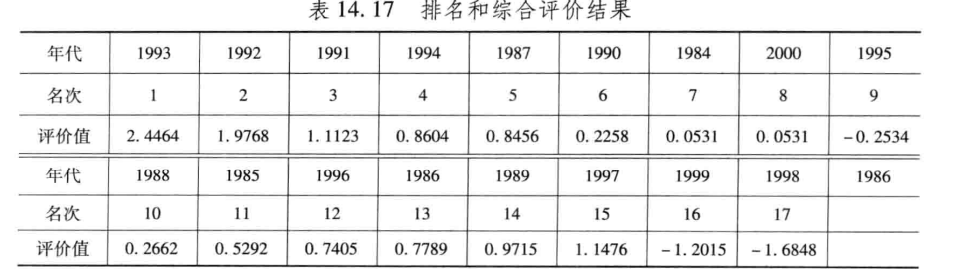
[stf, ind] = sort(tf, 'descend'); % 把得分按照从高到低的次序排列
stf = stf',ind = ind' %转置看起来方便些