图像频域处理之高斯滤波器「建议收藏」

在前两篇文章中，我们实现了图像的离散傅里叶变换与反变换，而这正是对图像频率域进行处理的前提。接下来这篇文章打算在已有工作的基础上实现高斯滤波器，对图像进行简单的频率域滤波。

一、频率域滤波基础

在上一篇关于FFT的文章中已经介绍到，相比于核数较大的空间域滤波来说，频率域滤波有着明显的优势。此外，频率域还有一些其他特性，如远离变换的原点时，低频对应于图像中变化缓慢的灰度分量；而更加远离原点时，较高的频率开始对应于图像中越来越快的灰度变化，它们是图像中由灰度急剧变化表征的物体边缘或其他分量。正是这些特性，能够让我们得到一些试验性的结果，后面我们可以看到。

那么如何进行频率域滤波呢。一般来说，其步骤是先修改一幅图像的傅里叶变换，然后计算其反变换，得到处理结果的空间域表示。因此，若已知大小为 $P\times Q$ 像素的一幅（经过填充的）数字图像 f(x,y) ,则我们感兴趣的基本滤波公式为

$g(x,y)=Real\left \{ \varsigma ^{-1}\left [ H(u,v)F(u,v) \right ] \right \}$

式中， $\varsigma ^{-1}$ 是IDFT， F(u,v) 是输入图像 f(x,y) 的DFT， H(u,v) 是滤波器传递函数（更常称滤波器或滤波器函数）， g(x,y) 是滤波后的（输出）图像。

简单来说，频率域的滤波过程可以总结为以下几步：1、进行傅里叶变换及中心化；2、构建一个传递函数 H(u,v) ；3、采用对应元素相乘得到；4、反变换得到滤波后的图像（注意这个仅是简化的步骤，在冈萨雷斯一书中，完整的步骤还包括处理前对图像进行填充以及处理后重新提取出来）。下面的代码展示了这个过程，FFT和IFFT使用的都是上一篇文章中我们自己实现的函数，可以点击这里了解。

#实现滤波
def filter(img, trans):
    #先转换至频域并中心化
    F = fft_2d(img)
    F_shift = fshift(F)
    
    #与传递函数对应元素相乘
    F_trans =  F_shift * trans
    
    #进行逆变换并得到实部
    img_out = np.abs(ifft_2d(ifshift(F_trans)))
    
    return img_out

二、高斯低通滤波器

可以看到，前面我们早就实现了傅里叶变换及反变换，现在最主要的问题就是构建滤波器函数。首先介绍低通滤波器，图像中的边缘和其他急剧的灰度变化（如噪声）主要影响其傅里叶变换的高频内容。因此，在频率域中时通过衰减高频（即低通滤波）来实现平滑模糊的。高斯低通滤波器（GLPF）传递函数有如下形式：

$H(u,v)=e^{-D^{2}(u,v)/2D^{2}_{0}}$ ，

式中， D(u,v) 是 $P\times Q$ 频率矩阵中心到矩阵中包含的任意一点 (u,v) 的距离。 $D_{0}$ 是截止频率，当 $D(u,v)=D_{0}$ 时，GLPF传递函数下降到其最大值1.0的0.607。下面显示了一个GLPF传递函数的透视图、图像和径向剖面。

图像频域处理之高斯滤波器「建议收藏」 — （a）一个GLPF传递函数的透视图；（b）以图像形式显示的函数；（c）不同D值的径向剖面

根据公式，代码实现如下。

#计算高斯低通滤波器的传递函数
def GLPF(h, w, D):
    #获取索引矩阵及中心点坐标
    x, y = np.mgrid[0:h, 0:w]
    center = (int((h-1)/2), int((w-1)/2))
     
    #计算中心距离矩阵
    dis_square = (x-center[0])**2 + (y-center[1])**2
     
    #计算变换矩阵
    transfor = np.exp(- dis_square / (2*D**2))
    
    return transfor

三、高斯高通滤波器

前面说过，衰减图像的傅里叶变换中的高频分量可以平滑图像。因为边缘和其他灰度的急剧变化与高频分量有关，因此可在频率域中通过高通滤波来实现图像锐化，高通滤波衰减傅里叶变换中的低频分量而不干扰高频信息。

高通滤波器的实现非常简单，在频率域中用1减去低通滤波器传递函数即可得到：

$H_{HP}(u,v)=1-H_{LP}(u,v)$

式中， $H_{LP}(u,v)$ 是低通滤波器的传递函数。因此，可得高斯高通滤波器（GHPF）的传递函数为

$H(u,v)=1-e^{-D^{2}(u,v)/2D^{2}_{0}}$

同样，下面展示了一个GHPF的透视图、图像和径向剖面。

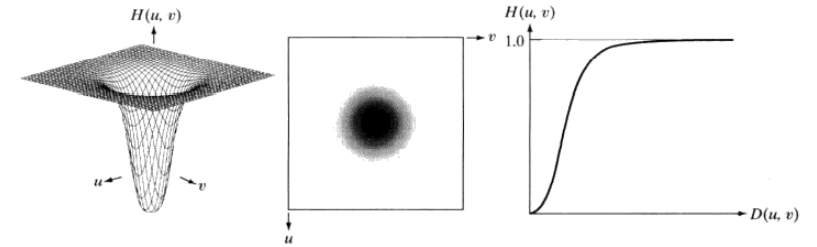
下面是GHPF的代码实现，可以看到只是最后用1减去了GLPF。

#计算高斯高通滤波器的传递函数
def GHPF(h, w, D):
    #获取索引矩阵及中心点坐标
    x, y = np.mgrid[0:h, 0:w]
    center = (int((h-1)/2), int((w-1)/2))
     
    #计算中心距离矩阵
    dis_square = (x-center[0])**2 + (y-center[1])**2
     
    #计算变换矩阵
    transfor = 1 - np.exp(- dis_square / (2*D**2))
    
    return transfor

四、效果展示

展示下实验效果，用两张不同的图片分别测试了原图以及 $D_{0}$ 值为2、5、10、20、50时两个滤波器的效果，可以明显看出低通滤波器能够使图像变得模糊平滑，而高通滤波器则是能够锐化图像。

五、多说两句

到此为止，我想写的关于图像处理领域的文章就写完了，后面这个专栏不会再更新了（大概），毕竟不管怎么说，图像处理也并不是我的兴趣领域。但如果后面同学有希望我介绍的东西，也可以私信或者发在评论区，我可以尽力去尝试一下。最后，这篇文章也参考了《冈萨雷斯数字图像处理（第四版）》一书，感谢前辈大佬的总结。

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容，请发送邮件至举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/10593.html