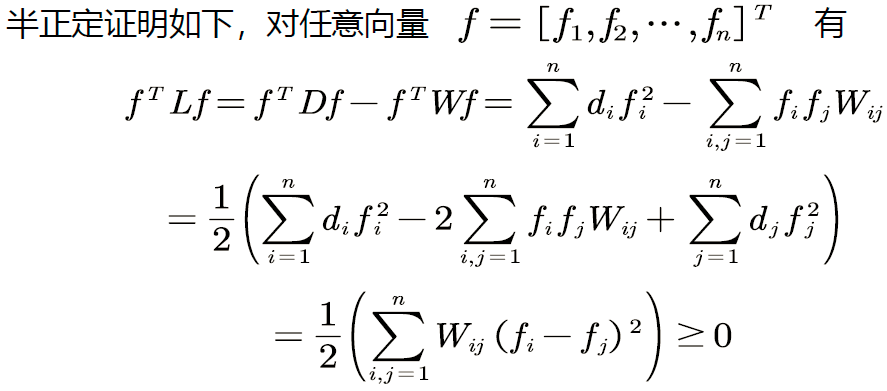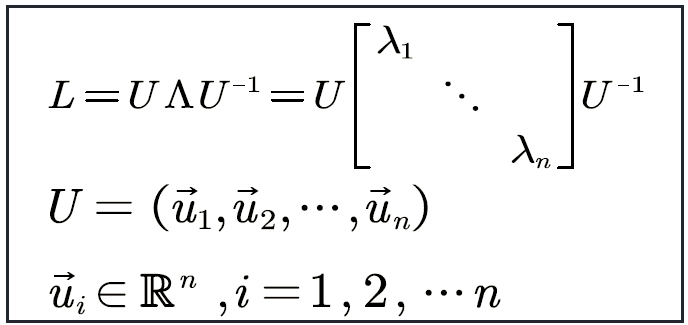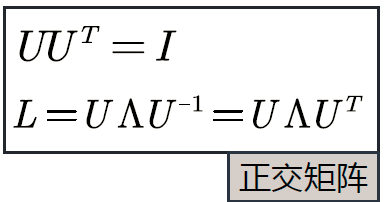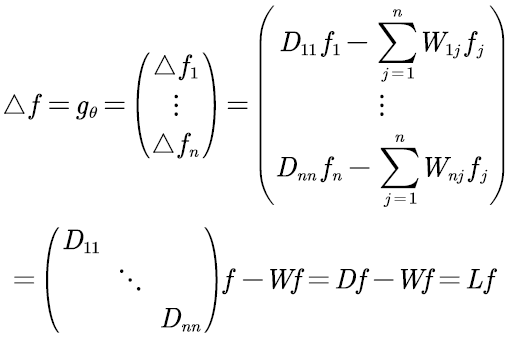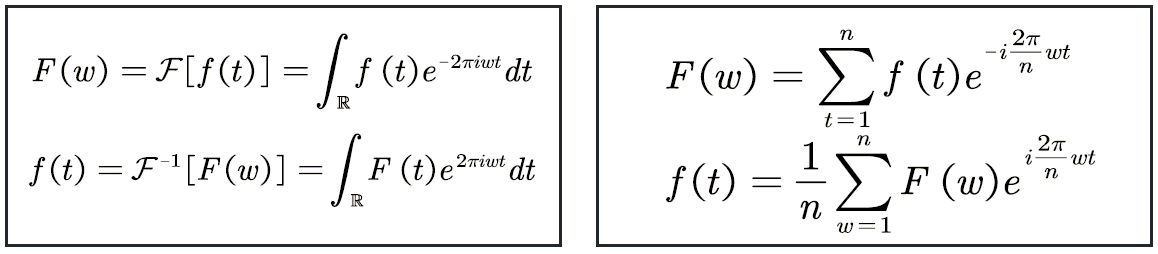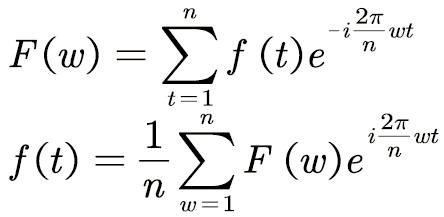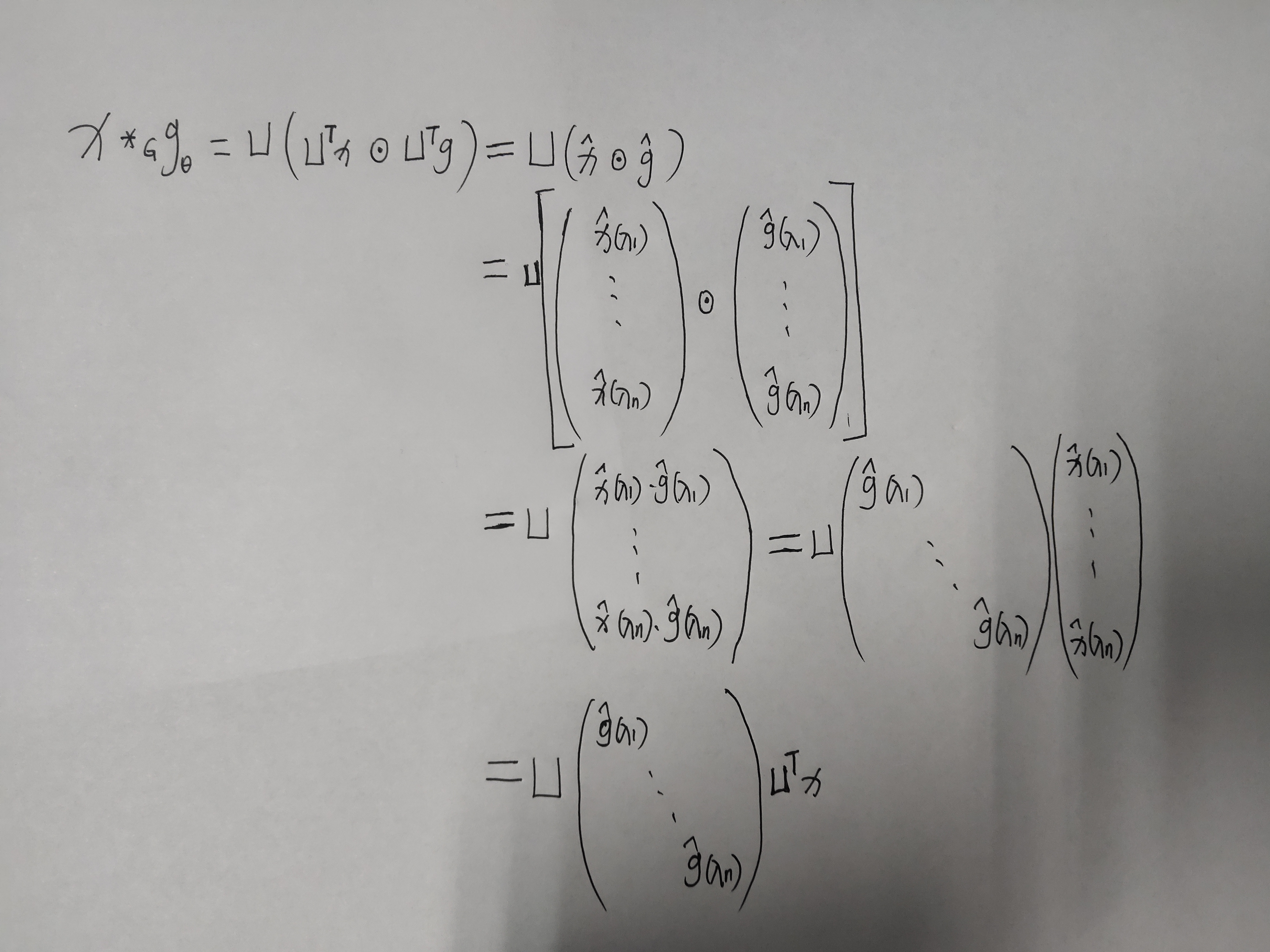第一章：卷积为什么要从 欧式空间 转到 非欧式空间.
第二章：谱域图卷积介绍（2）.

目录

• 一、图卷积介绍
• • 1.1 图卷积的由来
  • 1.2 经典卷积网络的局限
  • 1.3 图卷积分类
• 二、图谱卷积的背景知识
• • 2.1 谱域图卷积实现思路
  • 2.2 拉普拉斯矩阵（Laplacian Matrix）
  • • 2.2.1 拉普拉斯矩阵的定义：
    • • （1）符号设置
      • （2）拉普拉斯矩阵定义：
    • 2.2.2 拉普拉斯矩阵的性质：
    • 2.2.3 拉普拉斯矩阵的谱分解（特征分解）
    • 2.2.4 拉普拉斯矩阵与拉普拉斯算子
    • • （1）拉普拉斯算子：
      • （2）离散情况下欧氏空间的拉普拉斯算子：
      • （3）图上的拉普拉斯算子：
    • 2.2.5 总结：
  • 2.3 图傅里叶变换
  • • 2.3.1 图上的信号
    • 2.3.2 经典傅里叶变换
    • 2.3.3 图傅里叶变换
    • • （1）图傅里叶变换定义：
      • （2）图傅里叶反变换的定义：

一、图卷积介绍

1.1 图卷积的由来

我们都知道，卷积神经网络在语音、图像、视频取得了巨大成功（尤其是在图像上）。同时，图数据广泛存在于我们的生活中，如下图所示的几种数据集，就是图数据的代表：

因此，如何将卷积应用在不规则的图数据上，进而更好的处理图数据，就成了自然而然的想法了。
但是很可惜，经典的卷积网络有一个很明显的局限：那就是无法处理图结构数据。

1.2 经典卷积网络的局限

（1）➢ 只能处理固定输入维度的数据（维数一致性）；
（2）➢ 局部输入数据必须有序（序列有序性）。
语音、图像、视频（规则结构）满足以上两点要求。但并不适用于图结构数据（非欧空间数据）。
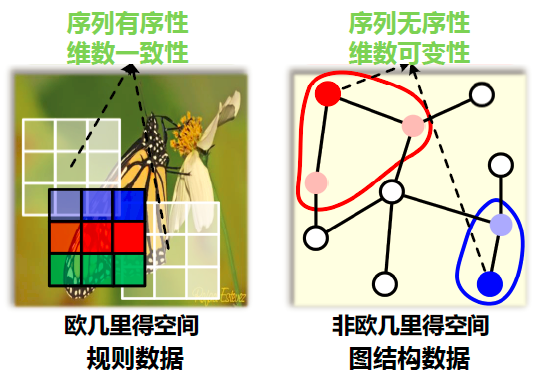
如下图所示，说明了欧式空间的规则数据和非欧空间的图数据最大的两点区别：

其中序列无序性是指：如上图中红色节点的邻居节点有两个，而我们不知道它们谁应该排在前，谁应该排在后，这就是序列无序性。
维数可变性是指：上图中红色节点和蓝色节点的邻居节点个数是可以不相同的，这就是维数可变性。

因此我们无法将3×3的卷积核应用到图数据上，这就是图卷积网络需要解决的问题。

1.3 图卷积分类

目前图卷积的实现，分为两大类：
（1）谱域图卷积：
➢ 根据 图谱理论 和 卷积定理 ，将数据由空域转换到谱域做处理 ，处理完再转换到空域。
➢有较为坚实的理论基础
（2）空域图卷积：
➢ 不依靠 图谱理论 和 卷积定理 ，直接在空间上定义卷积操作 。
➢ 定义直观 ，灵活性更强 。

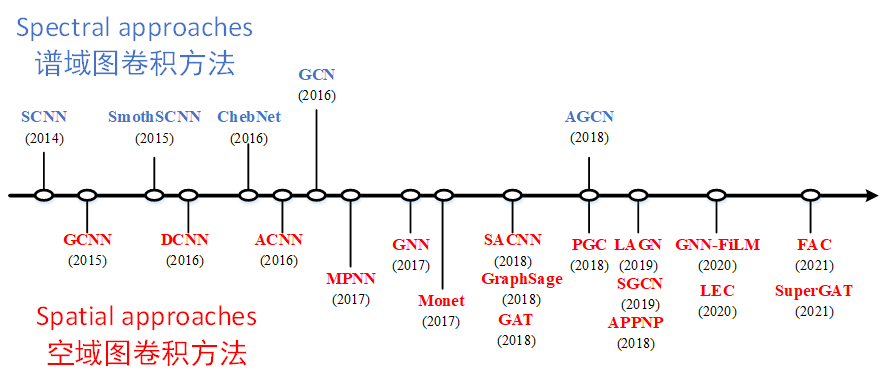
下面我总结了图卷积的一些部分经典模型：

接下来先介绍谱域图卷积方法，主要由SCNN、GCN和ChebNet三个模型引出。但在介绍图谱卷积之前，我们需要补充一下背景知识。因此，这篇文章接下来的部分，会介绍关于图谱卷积的所需要的背景知识，可能比较乏味。
但是只有掌握了这些知识，在下一篇文章中，才能开始介绍上述提到的三个模型。

二、图谱卷积的背景知识

2.1 谱域图卷积实现思路

要在图上实现卷积，我们就需要问一下，到底什么是卷积？
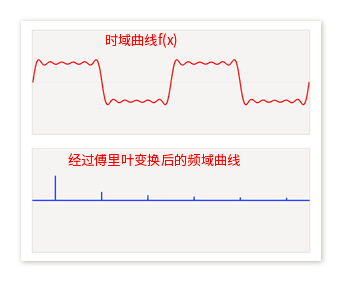
答：根据卷积定理，两信号在 空域 (或者时域)的卷积的傅里叶变换等于这两信号在频域中的傅里叶变换的乘积，即：

其中，$f(t)$为空域上的信号，$F_1(w)$为频域上的信号，$\mathcal{F}$为傅里叶变换，$\star$表示卷积操作，$\cdot$为乘积。
也可以写成：

其中，${\mathcal{F}}^{-1}$为傅里叶反变换。

因此，我们的卷积就是如下公式所示：

这个卷积的意思就是：
（1）将空域信号转换到频域（傅里叶变换实现），然后相乘。
（2）将相乘的结果再转换到空域（傅里叶反变换实现）。
解释：我们将$f_1(t)$定义为空域输入信号，$f_2(t)$定义为空域卷积核，那么卷积核就可以这样定义：
首先将空域上的信号$f_1(t)$转换到频域信号$F_1(w)$，然后相乘，再将相乘后的结果通过傅里叶反变换${\mathcal{F}}^{-1}$后，再返回空域上去，这个就是谱域图卷积的实现思路（将空域转换到频域上处理，处理完再返回）。

回想一下前面所说的经典的卷积操作具有序列有序性和维数不变性的限制，使得经典卷积难以处理图数据，也就是说对于一个3×3的卷积核，它的形状是固定的，它的感受野的中心节点必须要有八个领域才能使用卷积核，但是图上的节点的领域节点是不确定的，此外图上节点的领域节点也是没有顺序的，这就不能直接在空域使用经典的卷积。但是当我们把数据从空域转换到频域，在频域处理数据时，只需要将每个频域的分量放大或者缩小就可以了，不需要考虑信号在空域上存在的问题，这个就是谱域图卷积的巧妙之处。

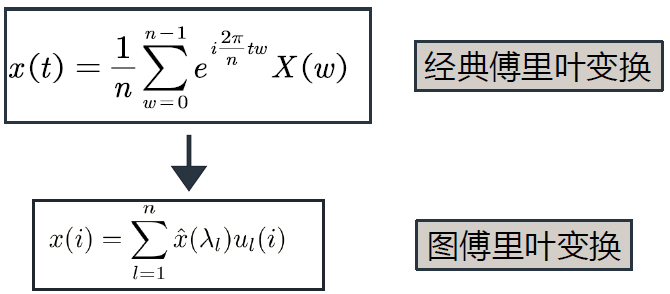
但是，随之而带来的问题是：图上的傅里叶变换和傅里叶反变换如何定义？
这里先给出结论，后面一步步证明。
结论：

为了证明图傅里叶变换，我们需要知道一些关于图的术语和相关数学知识，下面来看：

2.2 拉普拉斯矩阵（Laplacian Matrix）

2.2.1 拉普拉斯矩阵的定义：

（1）符号设置

无向图：$\mathcal{G}=(v,\epsilon ,w)$，$|v|=n$。
邻接矩阵：$W\in {\mathbb{R}}^{n\times n}$。
度矩阵：$D_{ii}=\sum _j{W}_{ij}$，$D\in {\mathbb{R}}^{n\times n}$。
其中,$v$代表所有节点的集合（共n个），$\epsilon$代表所有边的集合；$W$代表邻接矩阵（nxn的方阵）；$D$为度矩阵，定义为从$i$节点出发的所有边的权重之和（nxn的方阵，是对角矩阵）。
下面看一个例子，这个例子中的权重都为1：

在这个例子中，我们定义的拉普拉斯矩阵为：度矩阵减邻接矩阵。其实，拉普拉斯矩阵的定义有好几种，下面接着看：

（2）拉普拉斯矩阵定义：

这里要说明的是：常用的拉普拉斯矩阵实际有三种：

No.1： $L=D-A$，更专业的名称叫Combinatorial Laplacian；

No.2：$L^{sys}=D^{-1/2}L{D}^{-1/2}$，定义的叫Symmetric normalized Laplacian,很多GCN的论文中应用的是这种拉普拉斯矩阵；这里的$D^{-1/2}L{D}^{-1/2}$就是对$L$归一化，至于为什么两边乘以一个矩阵的逆就归一化了？这里需要复习到矩阵取逆的本质是做什么。
我们回顾下矩阵的逆的定义，对于式子$A\ast X=B$ ，假如我们希望求矩阵$X$，那么当然是令等式两边都乘以$A^{-1}$ ，然后式子就变成了$X=A^{-1}\ast A\ast X=A^{-1}\ast B$ 。
举个例子对于，单个节点运算来说，做归一化就是除以它节点的度，这样每一条邻接边信息传递的值就被规范化了，不会因为某一个节点有10条边而另一个只有1条边导致前者的影响力比后者大，因为做完归一化后者的权重只有0.1了，从单个节点上升到二维矩阵的运算，就是对矩阵求逆了，乘以矩阵的逆的本质，就是做矩阵除法完成归一化。但左右分别乘以节点$i$,$j$度的开方，就是考虑一条边的两边的点的度。
具体到每一个节点（拉普拉斯矩阵的元素级的定义）,对结点$i$,$j$,矩阵中的元素由下面的式子给出（对于无向无权图）：

其中$deg(v_i)$,$deg(v_j)$分别为节点$i$,$j$的度，也就是度矩阵在节点$i$,$j$处的值。

No.3：$L^{rw}=D^{-1}L，定义的叫RandomwalknormalizedLaplacian$

2.2.2 拉普拉斯矩阵的性质：

拉普拉斯矩阵是 对称半正定 矩阵。
证明：

上面是$L=D-A$的拉普拉斯矩阵半正定的证明，感兴趣的可以看看，其实就是展开了。
那我们得到$L$是 对称半正定矩阵 有什么用呢？为了得到这个答案，我们需要复习半正定矩阵的性质。

作为对称半正定矩阵，拉普拉斯矩阵 $L$ 有如下性质：

（1）➢ n阶对称矩阵一定有n个线性无关的特征向量。
（2）➢ 对称矩阵的不同特征值对应的特征向量相互正交，这些正交的特征向量构成的矩阵为正交矩阵。
（3）➢ 实对称矩阵的特征向量一定是实向量
（4）➢ 半正定矩阵的特征值一定非负。

拉普拉斯矩阵有了上面的性质，我们就可以进行拉普拉斯矩阵的谱分解了。

2.2.3 拉普拉斯矩阵的谱分解（特征分解）

特征分解（Eigen decomposition），又称谱分解（Spectral decomposition），是将矩阵分解为由其特征值和特征向量表示的矩阵之积的方法。

由于拉普拉斯矩阵是 对称半正定矩阵，因此，n阶对称矩阵一定有n个线性无关的特征向量（对称矩阵性质）。n维线性空间中的n个线性无关的向量都可以构成它的一组基（矩阵论知识）。
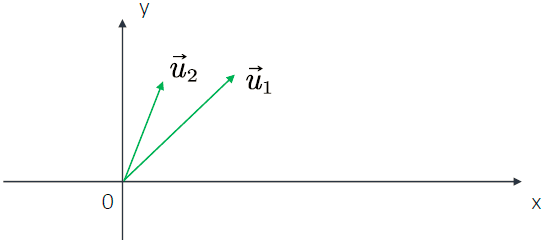
所以我们可以得出：拉普拉斯矩阵的n个特征向量是线性无关的，他们是n维空间中的一组基。如下图这样：在二维空间中有$u_1$,$u_2$两个线性无关的向量，则它们可以表示这个二维空间中的所有向量，它们就是二维空间中的一组基。

同时，对称矩阵的不同特征值对应的特征向量相互正交，这些正交的特征向量构成的矩阵为正交矩阵（对称矩阵性质）。
所以我们又可以得出：拉普拉斯矩阵的n个特征向量是n维空间中的一组标准正交基。如下图这样：

其实，前面就是在证明：拉普拉斯矩阵特征分解后的特征向量不但是n维空间中的一组基，而且还是正交的（相乘为0），简称标准正交基。
所以，拉普拉斯矩阵的谱分解就是如下形式（结论）：

简写为如下形式：

但是为什么拉普拉斯矩阵可以是度矩阵 减 邻接矩阵，也就是$L=D-W$呢？原因是拉普拉斯矩阵是图上的一种拉普拉斯算子，下面接着看什么是拉普拉斯算子：

2.2.4 拉普拉斯矩阵与拉普拉斯算子

（1）拉普拉斯算子：

拉普拉斯算子$△$定义为：梯度gradient $\nabla$的散度divergence$\nabla$$\cdot$ 。
即：

对于n维欧几里得空间，我们可以认为拉普拉斯算子是一个二阶微分算子。
即在各个维度求二阶导数后求和。

在3维欧几里得空间，对于一个三元函数$f(x,y,z)，$我们可以得到：

（2）离散情况下欧氏空间的拉普拉斯算子：

离散函数的一阶导数为：

离散函数的二阶导数为：

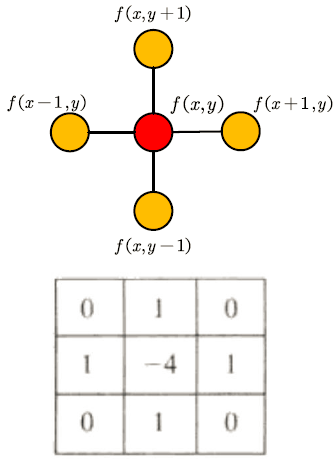
类似的，对于两个变量的函数（例如图像，如下图所示）：

在y方向也有：

那么两个变量的离散拉普拉斯算子可以写成：

那么，图上的拉普拉斯算子又是什么呢？

（3）图上的拉普拉斯算子：

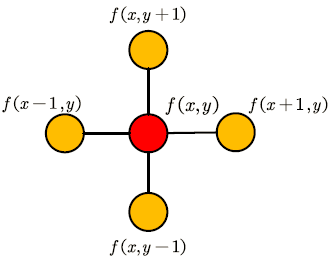
欧氏空间内，二维的拉普拉斯算子可以理解为中心节点与周围节点的差值，然后求和。如下图所示：

类似的，在图上的拉普拉斯算子可以定义如下：

其中，$f=(f_1,f_2,...,f_n)$，代表n个节点上每个节点的信号。
当有权重时：

可以理解为中心节点依次减去周围节点，乘以权重后，然后求和。因此，可以化简为如下这样：

对于n个节点，则可以写成如下这样：

因此，我们就可以得出结论：拉普斯矩阵是图上的一种拉普拉斯算子 。
可能对这个证明还不明白，其实只要记住结论也可以。如果还想了解更多：看 Discrete Regularization Weighted Graphs for Image and Mesh Filtering这篇文章 。

2.2.5 总结：

以上就是拉普拉斯矩阵的性质，正是因为有了这些性质，才会使用拉普拉斯矩阵来做以下的工作。
还记得我们 证明拉普拉斯矩阵的性质 是要干嘛吗？没错，就是要定义图上的傅里叶变换。

2.3 图傅里叶变换

接下来，我们先回顾所需知识点，之后再证明图上的傅里叶变换。

2.3.1 图上的信号

图上的信号一般表达为一个向量。假设有n个节点。我们将图上的信号记为：

每一个节点上有一个信号值，如下图所示，类似于图像上的像素值。$i$节点上的值为$x(i)=x_i$

上图中蓝色线段代表信号的大小，类似于图像上灰度图像像素，像素越高，画的这个线段越长。图上的信号也是类似的，只不过若一个信号有$c$个通道，那么$x=[x_1,x_2,...,x_n]\in R^{n\ast c}$，彩色图像有R,G,B三个通道，则$c=3$。下面为了讲解简单，我们先假设图上的一个信号只有一个通道，当然多个通道也是类似的。

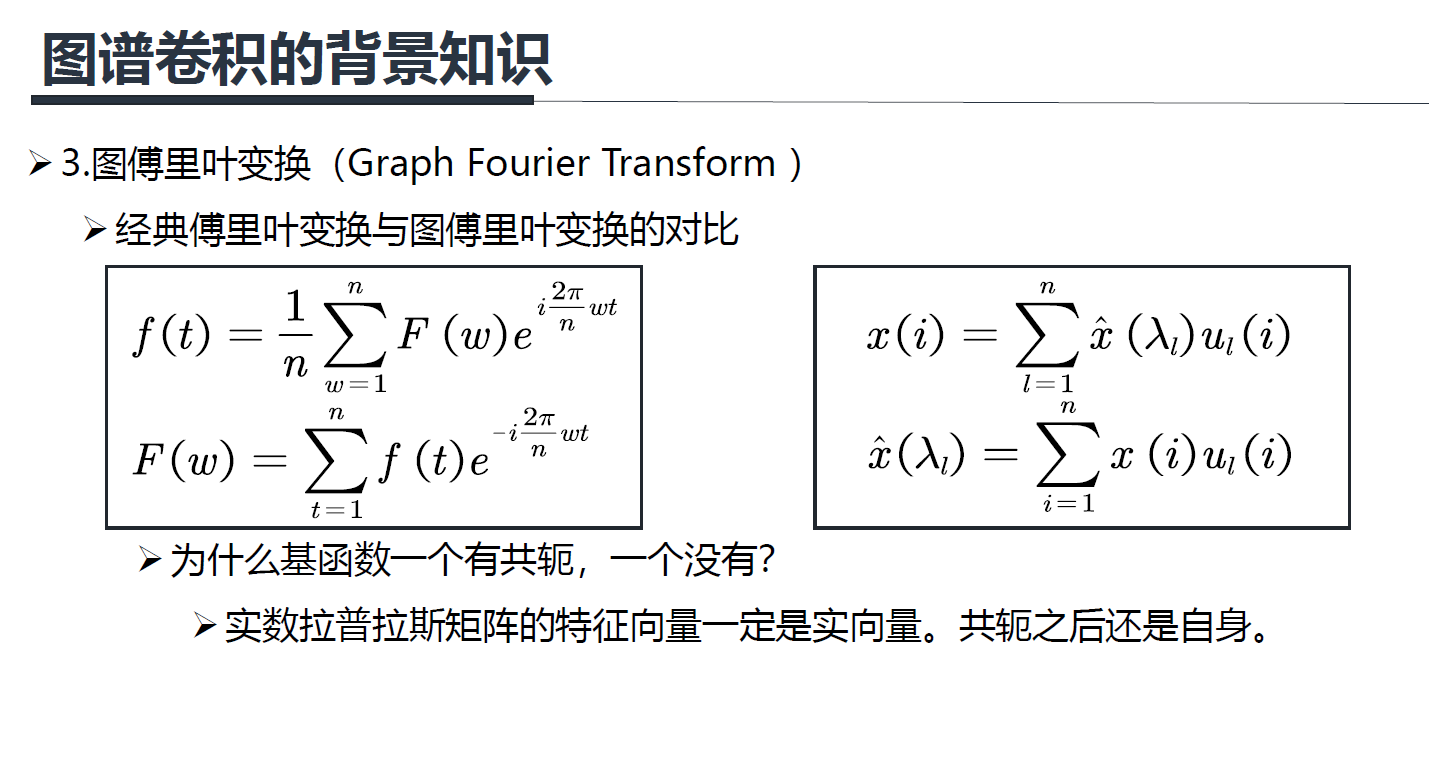
2.3.2 经典傅里叶变换

傅里叶变换的公式：

不了解经典傅里叶变换的可以去: https://zhuanlan.zhihu.com/p/19763358.查看，下面主要看看经典傅里叶变换的物理意义是什么。

傅里叶变换中不同频率的余弦函数可视为 基，其傅里叶系数表示基的振幅。如下图所展示的样子，相位在这个图中被忽略了 ，傅里叶系数实际上包含了振幅和相位 。

注：经典傅里叶变换其实就是说：一个信号由不同频率的基函数信号叠加而成，比如上图中红色信号是原信号，蓝色信号是不同频率上的基函数信号（余弦或者正弦函数）。上面图中，红色原信号可以由不同频率的基函数线性组合而成，蓝色的高度表示基前面的系数，也就是所谓的傅里叶系数，也就是原函数在这个基上的坐标分量。

➢傅里叶反变换的本质是：把任意一个函数表示成了若干正交基线性组合。
➢傅里叶正变换的本质是：求线性组合系数。具体做法是由原函数和基的 共轭的内积求得 。

上面的公式是离散的傅里叶变换，它和图傅里叶变换比较接近（图傅里叶变换也是离散的），$F(w)$就是上面所说的蓝线的高低。

2.3.3 图傅里叶变换

（1）图傅里叶变换定义：

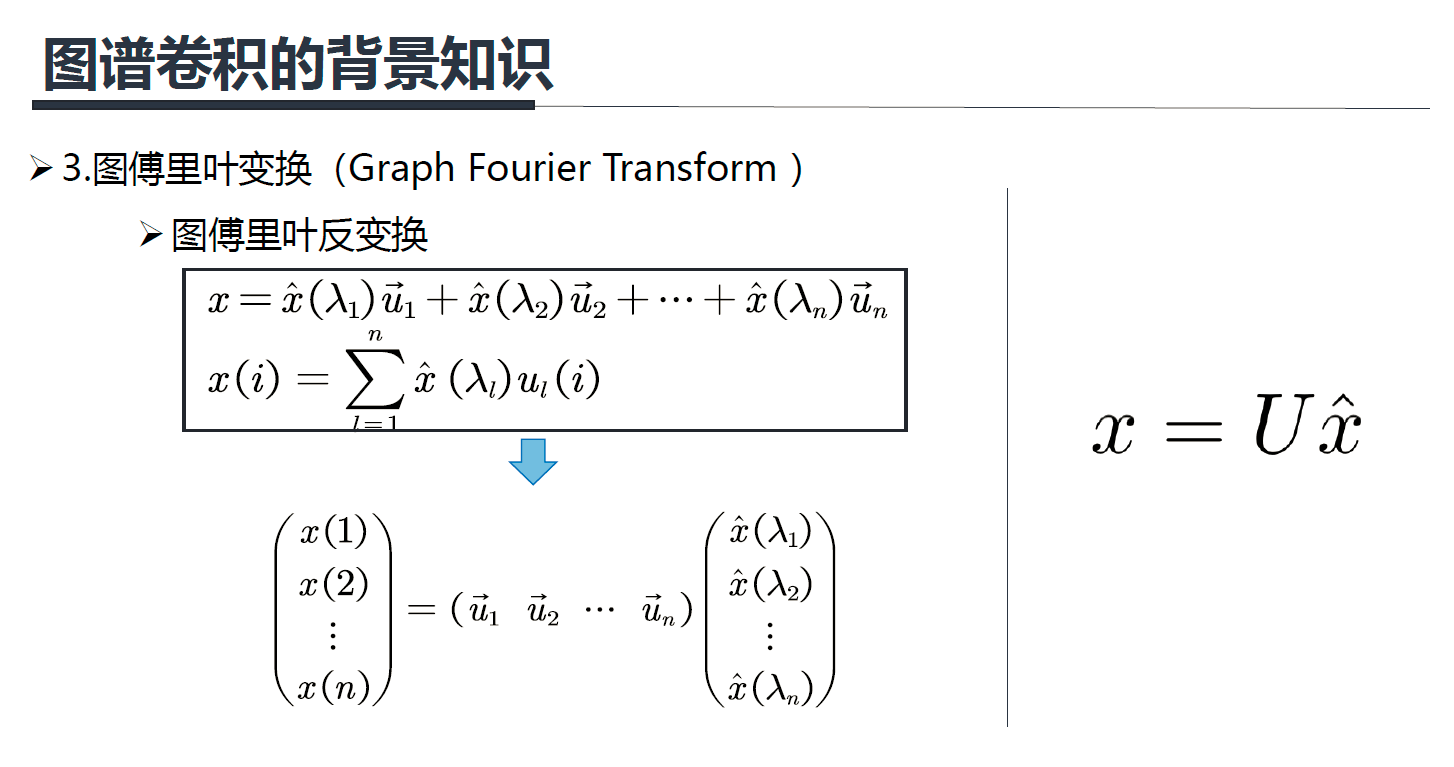
傅里叶反变换的本质是：把任意一个函数表示成了若干个正交基函数的线性组合。

上面左边公式是连续的傅里叶变换，右边是离散的。
对应graph上的信号$x\in \mathbb{R}$，如果要进行一个傅里叶变换，很自然的我们能想到：我们也要找到一组正交基，通过这组正交基的线性组合来表达$x\in \mathbb{R}$。
图傅里叶变换，实际上使用前面提到的拉普拉斯矩阵的特征向量，作为图傅里叶变换的基函数。

因此，使用拉普拉斯的特征向量作为基函数，任意的图上的信号可以表示为：

上面公式的$x$就是输入信号，$\hat{x}({\lambda }_1)$就是前面提到的傅里叶系数。

但是，这里有个疑问，为什么任意图上的信号$x\in \mathbb{R}$都可以表示成这样的线性组合？
答：原因在于
（1）拉普拉斯矩阵的特征向量$U=(u_1,u_2,...,u_n)$是n维空间中的n个线性无关的正交向量。
（2）n维空间中n个线性无关的向量可以构成空间的一组基（矩阵论知识），而且拉普拉斯矩阵的特征向量还是一组正交基。

（2）图傅里叶反变换的定义：

上面右边$x=U\hat{x}$ 中的 $\hat{x}$ 就是谱域上的信号。

傅里叶正变换就是求傅里叶反变换前面的系数，也就是每个基函数前面的振幅，具体做法看前面定义，也就是做输入信号 $x$ 和基函数 $u$ 的内积。

本征函数和本征向量可以认为是特征值和特征向量的扩展。特征向量是针对矩阵而言，而本征向量是针对算子而言的，很接近，宽泛一点可以认为是一个概念。

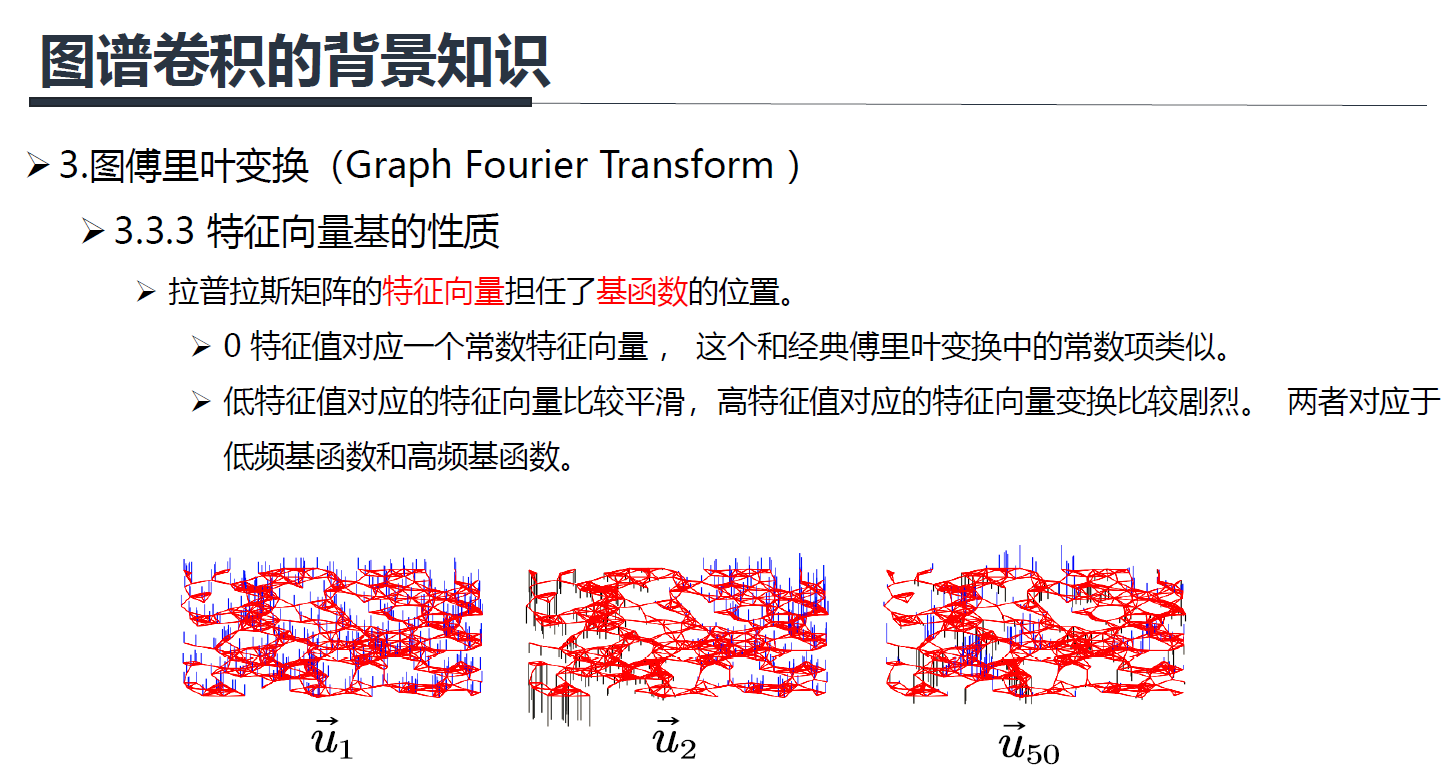
上图是三个不同的特征值对应的特征向量的示例，$u_1$是最小的特征值对应的特征向量（可以看出很平滑），$u_2$是第二小的特征值对应的特征向量（不太平滑），$u_{50}$是第五十小的特征值对应的特征向量（很不平滑）。

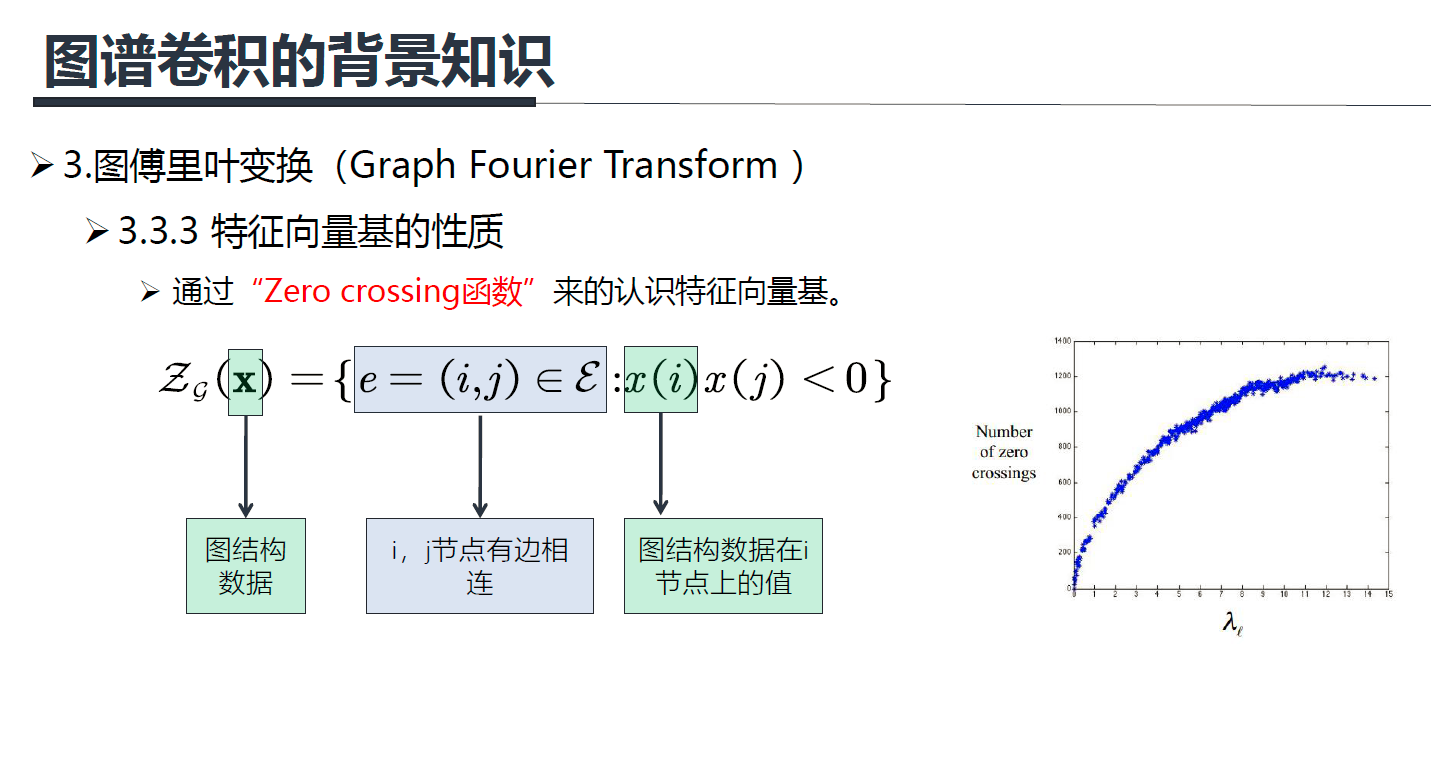
Zero crossing是指有边相邻的两个节点上对应的值一个大于0，一个小于0，每出现这样的一条边，Zero crossing就加一，通过Zero crossing的个数可以粗略的判断信号的震荡程度，或者可以说是平滑程度。从右图可以看到，大特征值可以视为高频信号，小特征值可以视为低频信号。

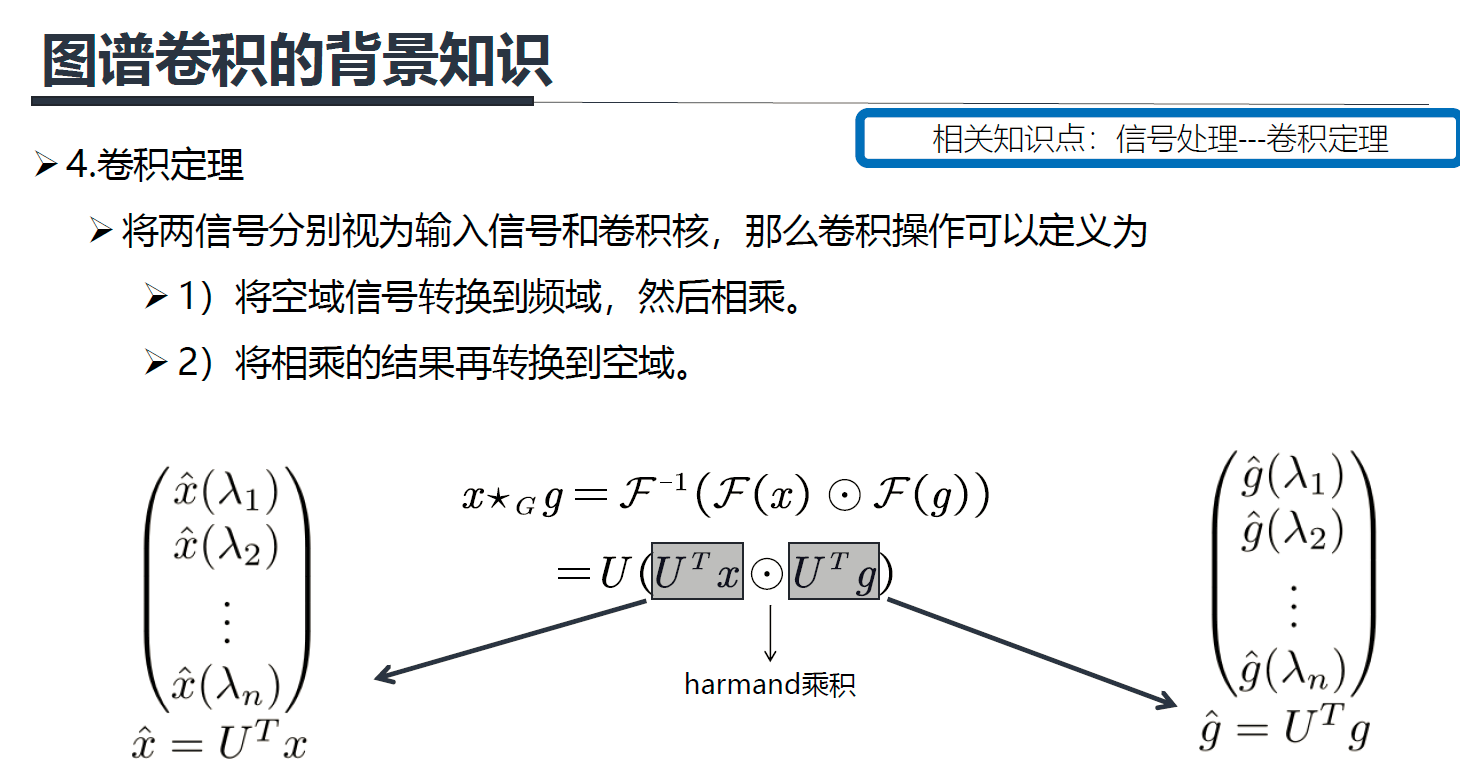
图上的卷积定义：先对$F(x)和F(g)$做傅里叶正变换，然后在谱域上做 $harmand$ 乘积，也就是$F(x)\odot F(g)$，
最后通过傅里叶反变换$F^{-1}$将结果返回到空域。前面讲了傅里叶正变换就是 $\hat{x}=U^{T}x$ ,则傅里叶反变换就是 $U(U^{T}x\odot U^{T}g)$。


上面这个推导感觉不是很好理解，我下面在清晰的推导一下（写公式费时间，手写一下），推导前提必须知道harmand的意思就是两个矩阵对应位置相乘（有区别与矩阵的乘法）。

上面就是谱域图卷积最终的公式，所有的谱域图卷积的原理就是这个公式，只是对滤波器 $\hat{g}$ 做了不同的处理。最后多说一下这个公式的意义是：卷积核信号（或者说滤波器信号）$\hat{g}$ 也是一个n维的向量，它的作用是将原信号的不同的分量进行一个放大或者缩小，这取决于卷积核信号在谱域上不同元素的值。