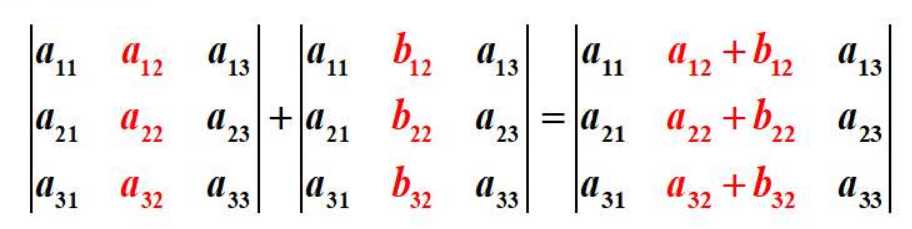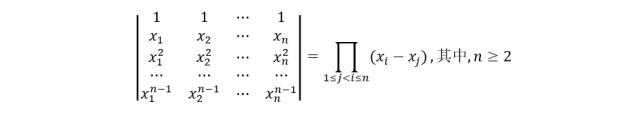1. 行列式发展史

1.1 行列式

• 行列式出现于线性方程组的求解，它最早是一种速记的表达式，在很长一段时间内，行列式只是作为解线性方程组的一种工具使用。现在行列式已经脱离线性方程组本身，成为数学中一种非常有用的工具。
• 1690年代，莱布尼茨和日本数学家关孝和于发明行列式
• 1750年，瑞士数学家克莱姆在其著作《线性代数分析导引》中，对行列式的定义和展开法则给出了比较完整、明确的阐述，并给出了现在我们所称的解线性方程组的克莱姆法则
• 稍后，数学家贝祖将确定行列式每一项符号的方法进行了系统化，利用系数行列式概念指出了如何判断一个齐次线性方程组有非零解
• 之后，法国数学家范德蒙德对行列式理论做出连贯的逻辑的阐述，把行列式理论与线性方程组求解相分离，他给出了用二阶子式和它们的余子式来展开行列式的法则。 1772 年，拉普拉斯在一篇论文中证明了范德蒙提出的一些规则，推广了行列式展开的方法。
• 1815 年，柯西在一篇论文中给出了行列式的第一个系统的、几乎是近代的处理。其中主要结果之一是行列式的乘法定理。另外，他第一个把行列式的元素排成方阵，采用双足标记法；引进了行列式特征方程的术语；给出了相似行列式概念；改进了拉普拉斯的行列式展开定理并给出了一个证明等。
• 继柯西之后，德国数学家雅可比引进了函数行列式，即 “雅可比行列式” ，指出函数行列式在多重积分的变量替换中的作用，给出了函数行列式的导数公式。雅可比的著名论文《论行列式的形成和性质》标志着行列式系统理论的建成。
• 19世纪，詹姆士·西尔维斯特提出配析法，并给出形成的行列式为零时两个多项式方程有公共根充分必要条件这一结果，但没有给出证明。
• 由于行列式在数学分析、几何学、线性方程组理论、二次型理论等多方面的应用，促使行列式理论自身在19世纪也得到了很大发展。整个19 世纪都有行列式的新结果。除了一般行列式的大量定理之外，还有许多有关特殊行列式的其他定理都相继得到。

1.2 从行列式到矩阵

• “矩阵” 这个词是由西尔维斯特首先使用的，他是为了将数字的矩形阵列区别于行列式而发明了这个述语。而实际上，矩阵这个课题在诞生之前就已经发展的很好了。从行列式的大量工作中明显的表现出来，为了很多目的，不管行列式的值是否与问题有关，方阵本身都可以研究和使用，矩阵的许多基本性质也是在行列式的发展中建立起来的。在逻辑上，矩阵的概念应先于行列式的概念，然而在历史上次序正好相反。
• 1858 年，英国数学家凯莱发表了《矩阵论的研究报告》，系统地阐述了关于矩阵的理论，首次把矩阵作为一个独立的数学概念提出来，并首先发表了关于这个题目的一系列文章

2. 行列式的本质定义

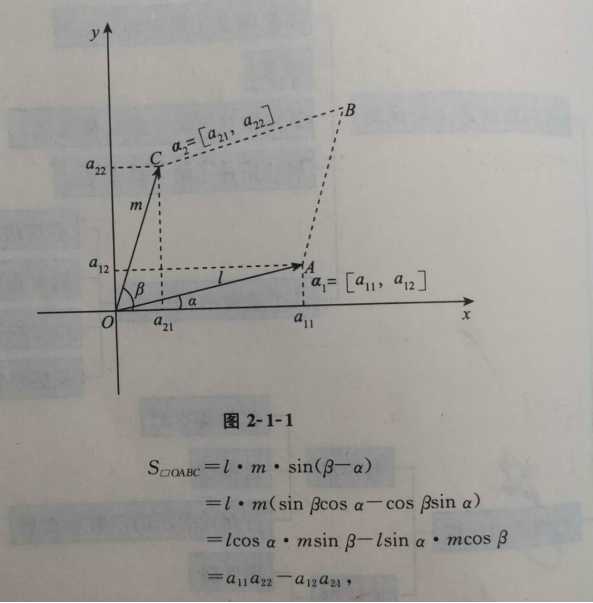
• 先从二维情况入手，一个2阶行列式 $D=\left|\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right|$，把它的第一行和第二行看成两个二维向量，$[a_{11},a_{12}]\stackrel{记}{=}{\alpha \text{α}\alpha }_1$ 和 $[a_{21},a_{22}]\stackrel{记}{=}{\alpha \text{α}\alpha }_2$，在直角坐标系中画出这两个向量如下
  
• 可见，2阶行列式 $\left|\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right|=a_{11}{a}_{22}-a_{12}{a}_{21}$ 的值就是其两个二维向量围成的平行四边形面积。行列式的一个特点是 “可以作线性推广”，因此3阶行列式的值是三个向量$[a_{11},a_{12},a_{13}]$，$[a_{21},a_{22},a_{23}]$，$[a_{31},a_{32},a_{33}]$为邻边的平行六面体的体积。
• 依此类推，可以给出n阶行列式$D_n$的本质定义：n阶行列式是由n个向量${\alpha }_1=[a_{11},a_{12},...,a_{1n}],{\alpha }_2=[a_{21},a_{22},...,a_{2n}],...,{\alpha }_n=[a_{n1},a_{n2},...,a_{nn}]$ 组成的，其（运算规则的）结果为这个n个向量为邻边的n维图形的体积
• 在学习行列式时，一个重要观点是：应该把行列式看作是由若干个向量拼成的，并且要把这些向量作运算

3. 线性方程组与行列式

• 行列式诞生自线性方程组。很长一段时间内，行列式只是作为解线性方程组的一种工具使用

3.1 系数行列式

1. 一个五元线性方程组的示例如下
   $$\{\begin{array}{c}{a}_{11}{x}_1+a_{12}{x}_2+a_{13}{x}_3+a_{14}{x}_4+a_{15}{x}_5=b_1\\ a_{21}{x}_1+a_{22}{x}_2+a_{23}{x}_3+a_{24}{x}_4+a_{15}{x}_5=b_2\\ ...\\ a_{51}{x}_1+a_{52}{x}_2+a_{53}{x}_3+a_{54}{x}_4+a_{55}{x}_5=b_5\end{array}$$

2. 提出系数部分，可得此线性方程组的系数行列式 $D$ 和系数矩阵 $A\text{A}A$，有$D=det(A\text{A}A)$
   $$D=\left|\begin{array}{ccccc}{a}_{11}& a_{12}& a_{13}& a_{14}& a_{15}\\ a_{21}& a_{22}& a_{23}& a_{24}& a_{25}\\ a_{31}& a_{32}& a_{33}& a_{34}& a_{35}\\ a_{41}& a_{42}& a_{43}& a_{44}& a_{45}\\ a_{51}& a_{52}& a_{53}& a_{54}& a_{55}\end{array}\right|$$
   $$A\text{A}A=\left[\begin{array}{ccccc}{a}_{11}& a_{12}& a_{13}& a_{14}& a_{15}\\ a_{21}& a_{22}& a_{23}& a_{24}& a_{25}\\ a_{31}& a_{32}& a_{33}& a_{34}& a_{35}\\ a_{41}& a_{42}& a_{43}& a_{44}& a_{45}\\ a_{51}& a_{52}& a_{53}& a_{54}& a_{55}\end{array}\right]$$

3. 提出结果部分，可得此线性方程组的结果向量 $b\text{b}b$
   $$b\text{b}b=\left[\begin{array}{c}{b}_1\\ b_2\\ b_3\\ b_4\\ b_5\end{array}\right]$$

4. 线性方程组的表示简化为 $Ax\text{Ax}Ax=b\text{b}b$

3.2 线性方程组的初等变换

• 在解线性方程组的过程中，可以通过一些变换简化方程形式，把一个方程组变成另一个同解方程组。这种不改变方程解的变换方式称为线性方程组的初等变换，一共有三种
  1. 互换：交换两个方程的位置
  2. 倍乘：把某个方程乘以一个非零常
  3. 倍加：把一个方程的 $k$ 倍加到另一个方程组上
• 我们小学学习的解多元一次方程组的方法，本质上就是不停使用初等变换进行消元求解

3.3 克莱姆法则（行列式的应用）

• 求解多元线性方程组是件麻烦事，1750年克莱姆提出的克莱姆法则为此提供了一个通解。
• 求解线性方程组、判断线性方程组解的情况，这是行列式最初的应用场景

3.3.1 用克莱姆法则解元线性方程组

• 克莱姆法则：一个含有N个未知量和N个方程的线性方程组，当系数行列式满足 $D\ne 0$ 时，有且仅有一个解
  $$x_1=\frac{D_1}{D}，x_2=\frac{D_2}{D}，...，x_n=\frac{D_n}{D}\text{\hspace{1em}(1–2)}$$

  其中$D_i$ 是将 $D$ 的第 j 列换成常数项 $b_1,b_2,...,b_n$ 而其余列不变的行列式，即
  $$D_j=\left|\begin{array}{ccccccc}{a}_{11}& \dots & a_{1,j-1}& b_1& a_{1,j+1}& \dots & a_{1n}\\ a_{21}& \dots & a_{2,j-1}& b_2& a_{2,j+1}& \dots & a_{2n}\\ ⋮& & ⋮& ⋮& ⋮& & ⋮\\ a_{n1}& \dots & a_{n,j-1}& b_n& a_{n,j+1}& \dots & a_{nn}\end{array}\right|=b_1{A}_{1j}+b_2{A}_{2j}+...+b_n{A}_{nj}(j=1,2,...,n)$$

  这里后面那个式子是按 $b$ 那一列展开的结果，后面再详细说明展开方法

3.3.2 证明克莱姆法则

1. 首先有原始线性方程组如下
   $$\{\begin{array}{c}{a}_{11}{x}_1+a_{12}{x}_2+...+a_{1n}{x}_n=b_1\\ a_{21}{x}_1+a_{22}{x}_2+...+a_{2n}{x}_n=b_2\\ \dots \\ a_{n1}{x}_1+a_{n2}{x}_2+...+a_{nn}{x}_n=b_n\end{array}$$

2. 通过初等变换（倍加），变为同解方程组
   $$\{\begin{array}{c}\begin{array}{r}{b}_{11}{x}_1+b_{12}{x}_2+...+b_{1n}{x}_n=c_1\\ b_{22}{x}_2+...+b_{2n}{x}_n=c_2\\ \dots \\ b_{nn}{x}_n=c_n\end{array}\end{array}$$

3. 再进行倍加，从下到上消元，得到同解方程组
   $$\{\begin{array}{c}\begin{array}{r}{a}_1{x}_1=d_1\\ a_2{x}_2=d_2\\ \dots \\ a_n{x}_n=d_n\end{array}\end{array}$$

4. 由行列式性质，有
   $$D=\left|\begin{array}{cccc}{a}_1& & & \\ & a_2& & \\ & & \ddots & \\ & & & a_n\end{array}\right|=a_1{a}_2...a_n$$
   $$D_1=\left|\begin{array}{cccc}{d}_1& & & \\ d_2& a_2& & \\ ⋮& & \ddots & \\ d_n& & & a_n\end{array}\right|=d_1{a}_2...a_n$$
   $$D_2=\left|\begin{array}{cccc}{a}_1& d_1& & \\ & d_2& & \\ & ⋮& \ddots & \\ & d_n& & a_n\end{array}\right|=a_1{d}_2...a_n$$
   $$D_n=\left|\begin{array}{cccc}{a}_1& & & d_1\\ & \ddots & & ⋮\\ & & a_{n-1}& d_{n-1}\\ & & & d_n\end{array}\right|=a_1...a_{n-1}{d}_n$$
   于是，若原方程组线性无关，则方程组的唯一解为
   $$x_1=\frac{d_1}{a_1}=\frac{D_1}{D}，x_2=\frac{d_2}{a_2}=\frac{D_2}{D}，...，x_n=\frac{d_n}{a_n}=\frac{D_n}{D}$$

3.4 线性相关与线性无关

• 利用克莱姆法则，我们可以方便地判断一个齐次线性方程组有非零解
  1. 有齐次线性方程组形式如下，注意所有式子等号右侧都是0
     $$\{\begin{array}{c}{a}_{11}{x}_1+a_{12}{x}_2+...+a_{1n}{x}_n=0\\ a_{21}{x}_1+a_{22}{x}_2+...+a_{2n}{x}_n=0\\ \dots \\ a_{n1}{x}_1+a_{n2}{x}_2+...+a_{nn}{x}_n=0\end{array}$$
  2. 判别定理：齐次线性方程组有非零解$\iff$ 方程组系数行列式 D = 0
  3. 证明（以下 $|a_{ij}{|}_n$ 代表系数行列式D）：
• 讨论说明

  1. 解的讨论
     

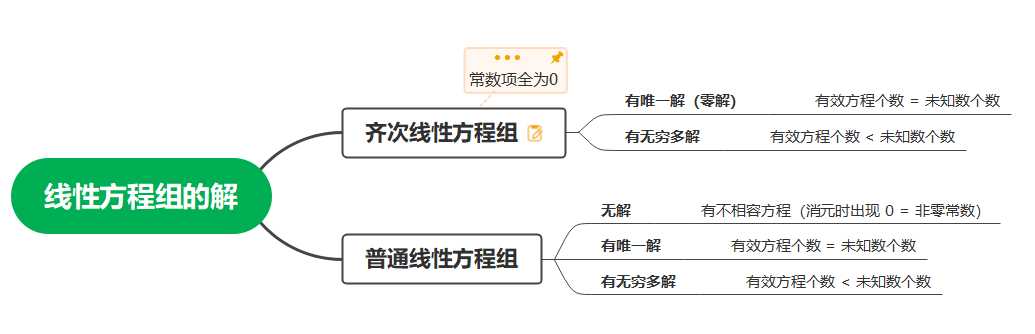
  2. 只要有效方程个数 = 未知数个数，线性方程组必有唯一解，对于齐次线性方程组，这个唯一解就是零解。

  3. 如果齐次线性方程组中出现非零解

     1. 意味着这里有效方程数量不足
     2. 字面上方程和未知数数量相同，故一定有某些方程能被其他方程线性表示，这种情况称为线性相关
     3. 所以消元后的同解线性方程组的系数行列式D中出现了全0行
     4. 根据行列式性质，D=0

     因此我们可以用系数行列式 $D$ 是否为0来判断齐次线性方程组是否有非零解。通常我们不关注行列式的具体值，而只关注系数行列式是否为0

  4. 线性相关和线性无关

     1. 说白了就是，如果一个方程组中，某个方程可以被其他方程通过倍乘和相加的方式（线性变换）表示出来，就说这些方程线性相关；反之称为线性无关
     2. 考虑系数行列式 $D$，对于 $D=0$ 的情况，我们通常不说方程线性相关，而说这里的行/列向量线性相关（意思其实就也是某一个向量可以用其他的线性表示）；反之若 $D\ne 0$ ，就称行/列向量线性无关
     3. 从几何角度看：$D=0$ 线性相关，代表向量间没有夹角，有同方向向量存在，无法围成封闭的n维图形体积，体积为0；$D\ne 0$ 线性无关，代表向量间有夹角，可以围成封闭的n维图形体积，体积不为0。

4. 行列式的性质

1. 行列互换，其值不变，即$|A|=|A^T|$，行列地位相等。

   • 可以从几何角度验证

2. 行列式中某行（列）元素全0，则行列式为0

   • 从几何角度看，某个向量边长为0，无法围成封闭的集合体
   • 从线性方程组看，某个方程组系数全为0，有效方程数量少于未知数个数，线性相关，存在非零解

3. 行列式中某行（列）元素有公因子k(k≠0)，则k可以提到行列式外部（行列式的值变成k倍）

   • 从几何角度看，k倍体积，只需要把某个边长度延长k倍
   • 从线性方程组看，倍乘是初等变换，不影响解情况

4. 行列式中某行（列）元素均是两个元素之和，则可以拆成两个行列式之和

   • 从几何角度看，这是把一个四边形/立方体垂直某边/棱切成两个
     

5. 行列式中两行（列）互换，行列式的值反号

   • 可以从几何角度验证
   • 从线性方程组看，互换是初等变换，不影响解情况
   • 可以用性质7和性质3推出

6. 行列式中的两行（列）元素相等或对应成比例，则行列式值为0

   • 从几何角度看，有两个平行边，无法围成封闭立方体
   • 这条和性质2差不多

7. 行列式中某行（列）的k倍加到令一行（列），行列式的值不变

   • 从几何角度看，这是把某条边延其向量指向平移了一段，体积不变
   • 从线性方程组看，倍加是初等变换，不影响解情况
   • 可以用性质4拆开，变成原行列式加一个性质6中的行列式（值为0）

5. 行列式的逆序数定义

• 在各大教科书里，通常都是直接给出这种逆序数定义，这种定义来自行列式的第二公理化构造，它其实是从对行列式符合的公理化条件里推导出来的一个结果，所以很不直观，用得也很少。对于这个推导，可以参考：线性代数拾遗（1）—— 行列式的三种公理化构造

5.1 逆序和排列

• 定义：
  
• 说明：逆序数描述了一组标准正交基 $p=(e_1,e_2,...,e_n)$，其置换 $p_1=(e_{i_1},e_{i_2},...,e_{i_n})$ 要经过几次两两对换才能变回 $p$ 本身

5.2 $n$ 阶行列式的定义

• $n\ge 2$ 阶行列式定义如下
  $$A=\left|\begin{array}{cccc}{a}_{11}& a_{12}& \dots & a_{1n}\\ a_{21}& a_{22}& \dots & a_{2n}\\ ⋮& ⋮& & ⋮\\ a_{n1}& a_{n2}& \dots & a_{nn}\end{array}\right|=\sum _{j_1{j}_2...j_n}(-1{)}^{\tau (j_1{j}_2...j_n)}{a}_{1j_1}{a}_{2j_2}...a_{n{j}_n}$$
  这里 ${\sum }_{j_1{j}_2...j_n}$ 表示对所有n个列下标排列求和，故为 $n!$ 项之和，注意到行下标已经顺序，而列下标是任意个级排列，故每项是由取自不同行不同列的 n 个元素的乘积组成，每项的正负号取决于 $(-1{)}^{\tau (j_1{j}_2...j_n)}$。当列下标为奇排列时，应附加负号；当列下标为偶排列时，应附加正号
  

6. 行列式的展开定理（第三种定义）

• 行列式可以按行或列展开，这其实来自其第三公理化定义

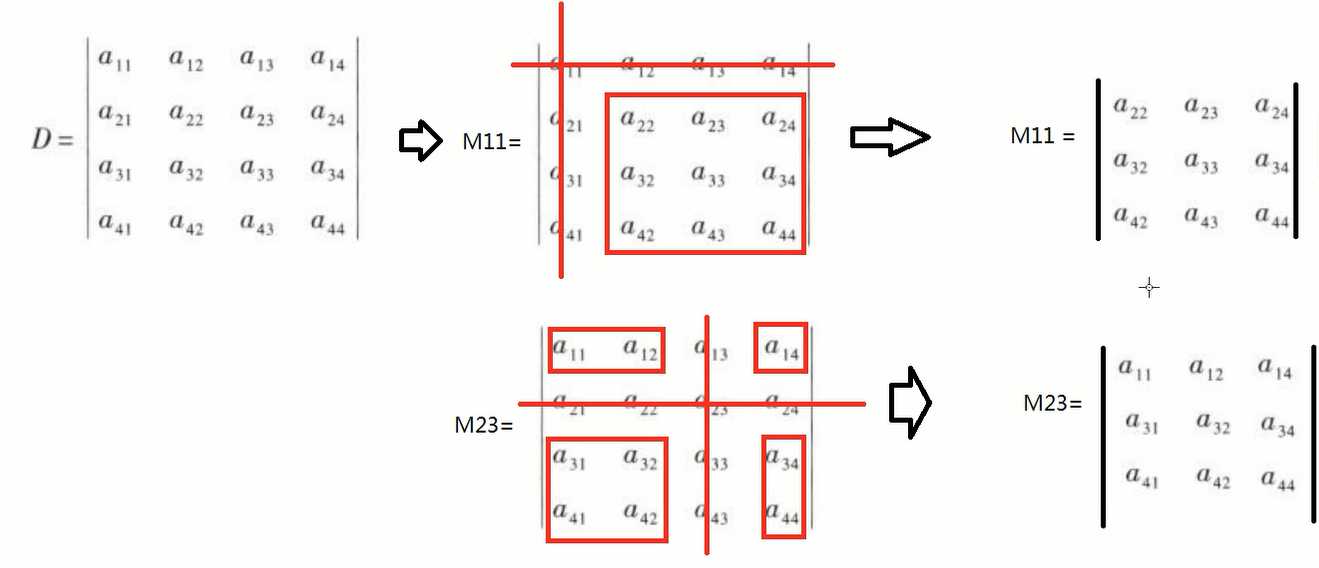
6.1 余子式

1. 余子式：在n阶行列式中，划去元$a_{ij}$所在的第i行与第j列的元，剩下的元不改变原来的顺序所构成的n-1阶行列式称为元$a_{ij}$的余子式，记作$M_{ij}$，即
   
2. 代数余子式：余子式乘上$(-1{)}^{i+j}$后称为$a_{ij}$的代数余子式，记作$A_{ij}$，即
   $$A_{ij}=(-1{)}^{i+j}{M}_{ij}$$
   显然也有
   $$M_{ij}=(-1{)}^{i+j}{A}_{ij}$$

6.2 行列式按某行（列）展开公式

• 行列式的值等于行列式的某行（列）元素分别乘以其相应的代数余子式后再求和，即
  $$|A|=\{\begin{array}{ccc}& 按第i行展开：& a_{i1}{A}_{i1}+a_{i2}{A}_{i2}+...+a_{in}{A}_{in}=\sum _{j=1}^n{a}_{ij}{A}_{ij}(i=1,2,...,n)\\ & 按第j列展开：& a_{1j}{A}_{1j}+a_{2j}{A}_{2j}+...+a_{nj}{A}_{nj}=\sum _{i=1}^n{a}_{ij}{A}_{ij}(j=1,2,...,n)\end{array}$$
  这样可以把一个n阶行列式转化为n个(n-1)阶行列式，实现降阶，直到最后可以用交叉技巧求解

• 行列式的某行（列）元素分别乘以另一行（列）元素的代数余子式后再求和，结果为0
  $$\begin{gathered} a_{i1}{A}_{k1}+a_{i2}{A}_{k2}+...+a_{in}{A}_{kn}=0,i\ne k \\ {a}_{1j}{A}_{1k}+a_{2j}{A}_{2k}+...+a_{nj}{A}_{nk}=0,j\ne k \end{gathered}$$
  分析一下第一行的式子，使用第 $i$ 行元素乘以第 $k$ 行代数余子式，就相当于把原行列式中第 $k$ 行内容替换为第 $i$ 行内容，再按第 $k$ 行展开，这个行列式中出现了两行相同，自然结果为 0

7. 几个重要的行列式

• 记住以下重要行列式，可以方便我们快速计算行列式的值

7.1 三角行列式

7.2 拉普拉斯展开

• 设 $A\text{A}A$ 为m阶矩阵，$B\text{B}B$ 为n阶矩阵，$O\text{O}O$ 代表全0阵，则
  $$\left|\begin{array}{cc}A& O\\ O& B\end{array}\right|=\left|\begin{array}{cc}A& C\\ O& B\end{array}\right|=\left|\begin{array}{cc}A& O\\ C& B\end{array}\right|=|A||B|$$
  $$\left|\begin{array}{cc}O& A\\ B& O\end{array}\right|=\left|\begin{array}{cc}C& A\\ B& O\end{array}\right|=\left|\begin{array}{cc}O& A\\ B& C\end{array}\right|=(-1{)}^{mn}|A||B|$$

7.3 范德蒙德行列式

今天的文章线性代数（1）—— 行列式分享到此就结束了，感谢您的阅读。