【算法】JavaScript必会算法 —— 排列组合（全排列）

首先理解一下排列组合的定义：

• 排列的定义：从$n$个不同元素中，任取$m$（$m\le n$，$m$与$n$均为自然数，下同）个元素按照一定的顺序排成一列，叫做从$n$个不同元素中取出$m$个元素的一个排列；从$n$个不同元素中取出$m(m\le n)$个元素的所有排列的个数，叫做从$n$个不同元素中取出$m$个元素的排列数，用符号$A_n^m$表示。此外规定$0!=1$
• 计算公式：$$A_n^m=n\times (n-1)\times (n-2)\times \dots \times (n-m+1)=\frac{n!}{(n-m)!}$$
• 组合的定义：从$n$个不同元素中，任取$m(m\le n)$个元素并成一组，叫做从$n$个不同元素中取出$m$个元素的一个组合；从$n$个不同元素中取出$m(m\le n）$个元素的所有组合的个数，叫做从$n$个不同元素中取出$m$个元素的组合数。用符号 $C_n^m$表示。
• 计算公式：$$C_n^m=\frac{A_n^m}{m!}=\frac{n!}{m!\times (n-m)!}$$
• 排列和组合的区别：看问题是否和顺序有关。有关就是排列，无关就是组合。

• 排列组合_360百科

接下来进入正题：

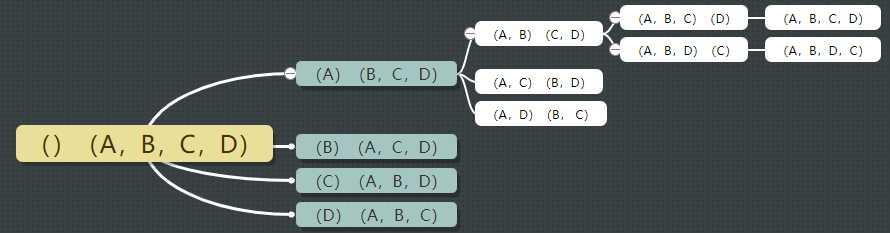
在一个数组arr中四个元素，现需要得到它们全排列的结果：即如下图所示得到$A_4^4=4\times 3\times 2\times 1=24$个结果

算法过程如图：

代码：

let func = (arr) => { 
   
  let len = arr.length
  let res = [] // 所有排列结果
  /** * 【全排列算法】 * 说明：arrange用来对arr中的元素进行排列组合，将排列好的各个结果存在新数组中 * @param tempArr：排列好的元素 * @param leftArr：待排列元素 */
  let arrange = (tempArr, leftArr) => { 
   
    if (tempArr.length === len) { 
    // 这里就是递归结束的地方
      // res.push(tempArr) // 得到全排列的每个元素都是数组
      res.push(tempArr.join('')) // 得到全排列的每个元素都是字符串
    } else { 
   
      leftArr.forEach((item, index) => { 
   
        let temp = [].concat(leftArr)
        temp.splice(index, 1)
        // 此时，第一个参数是当前分离出的元素所在数组；第二个参数temp是传入的leftArr去掉第一个后的结果
        arrange(tempArr.concat(item), temp) // 这里使用了递归
      })
    }
  }
  arrange([], arr)
  return res
}
console.log('结果：', func(['A', 'B', 'C', 'D']))

摘自极客时间王争老师的《数据结构与算法之美》专栏：

• 写递归代码的关键就是找到如何将大问题分解为小问题的规律，并且基于此写出递推公式，然后再推敲终止条件，最后将递推公式和终止条件翻译成代码。
• 编写递归代码的关键是，只要遇到递归，我们就把它抽象成一个递推公式，不用想一层层的调用关系，不要试图用人脑去分解递归的每个步骤。

• 轻松理解全排列算法的递归解法_jiaobuchong的专栏-CSDN博客

今天的文章【算法】JavaScript必会算法 —— 排列组合（全排列）分享到此就结束了，感谢您的阅读。