目录
a. 基本随机数
Matlab 中有两个最基本生成随机数的函数。
1.rand()
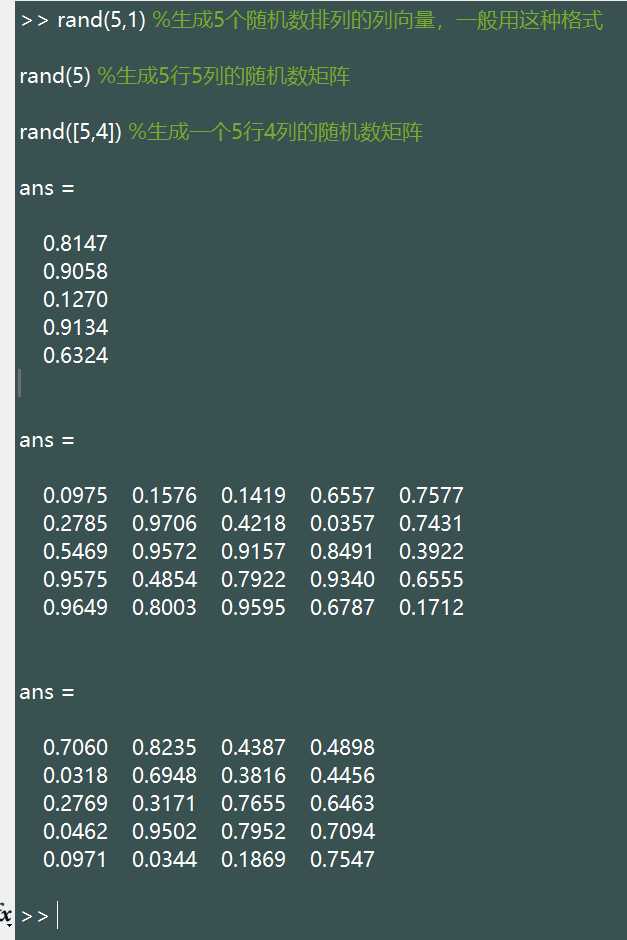
生成(0,1)区间上均匀分布的随机变量。基本语法:
rand([M,N,P ...])生成排列成 M*N*P… 多维向量的随机数。如果只写 M,则生成 M*M 矩阵;如果参数为 [M,N] 可以省略掉方括号。例如:
通过下面代码,可以生成大量随机数,查看大致的分布情况:
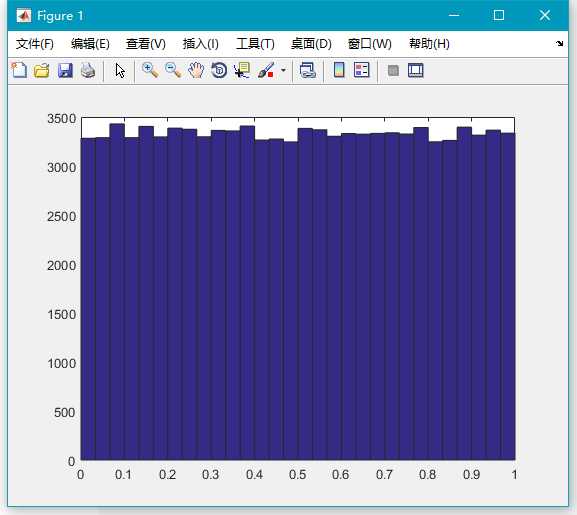
x=rand(100000,1);
hist(x,30);由此可以看到生成的随机数很符合均匀分布。
2.randn()
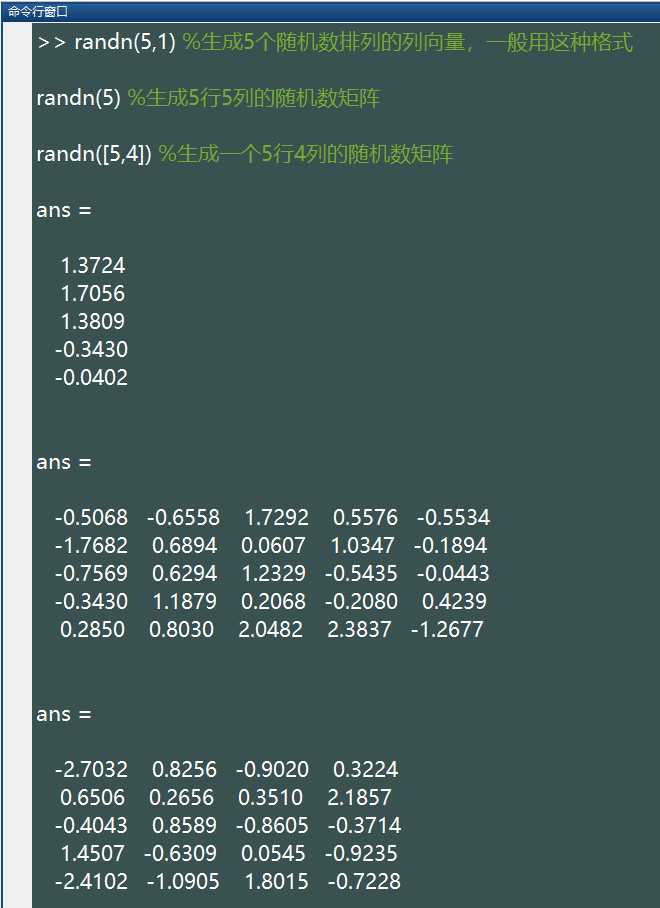
生成服从标准正态分布(均值为 0,方差为 1)的随机数。基本语法和 rand() 类似。
randn([M,N,P ...])生成排列成 M*N*P… 多维向量的随机数。如果只写 M,则生成 M*M 矩阵;如果参数为 [M,N] 可以省略掉方括号。例如:
通过下面代码,可以生成大量随机数,查看大致的分布情况:
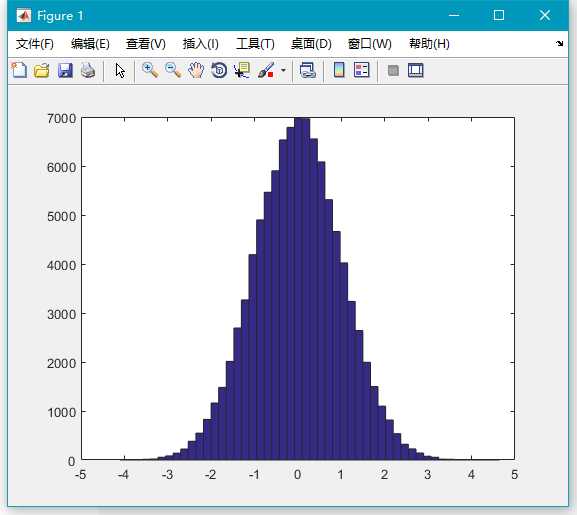
x=randn(100000,1);
hist(x,50);由图可以看到生成的随机数很符合标准正态分布。
b. 连续型分布随机数
如果你安装了统计工具箱(Statistic Toolbox),除了这两种基本分布外,还可以用 Matlab 内部函数生成符合下面这些分布的随机数。
3.unifrnd()
这个函数生成某个区间内均匀分布的随机数。基本语法
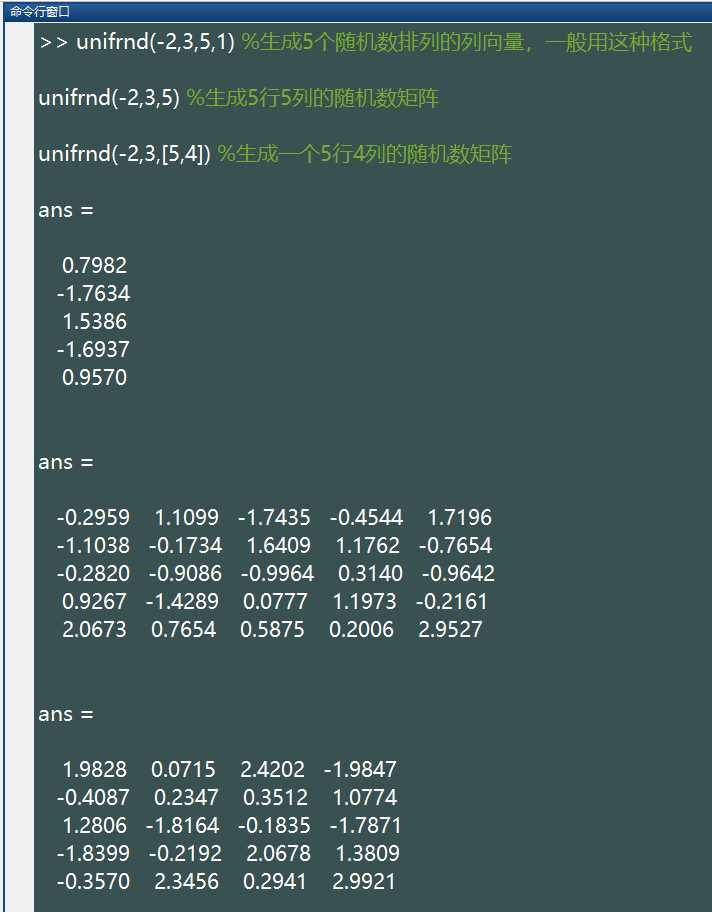
unifrnd(a,b,[M,N,P,...])生成的随机数区间在 (a,b) 内,排列成 M*N*P… 多维向量。如果只写 M,则生成 M*M 矩阵;如果参数为 [M,N] 可以省略掉方括号。例如:
%注:上述语句生成的随机数都在 (-2,3) 区间内.
通过下面代码,可以生成大量随机数,查看大致的分布情况:
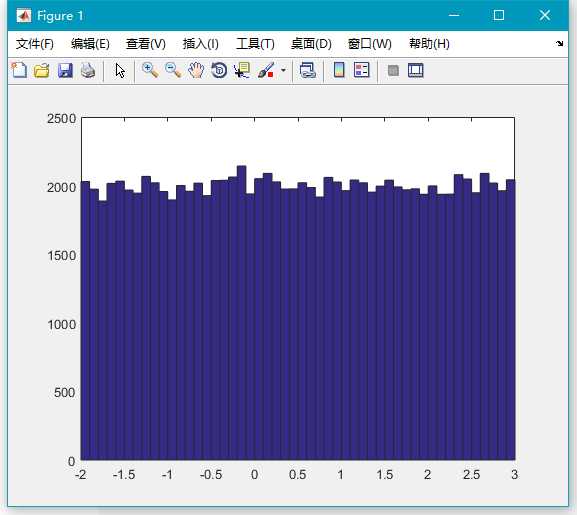
x=unifrnd(-2,3,100000,1);
hist(x,50);由图可以看到生成的随机数很符合区间 (-2,3) 上面的均匀分布。
4.normrnd()
此函数生成指定均值、标准差的正态分布的随机数。基本语法
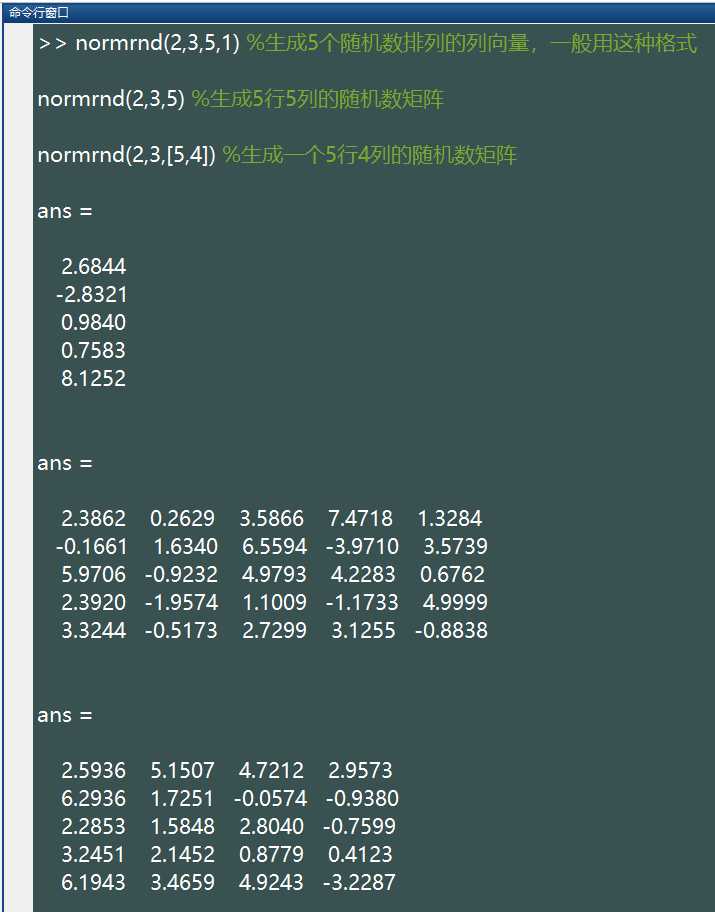
normrnd(mu,sigma,[M,N,P,...])生成的随机数服从均值为 mu,标准差为 sigma(注意标准差是正数)正态分布,这些随机数排列成 M*N*P… 多维向量。如果只写 M,则生成 M*M 矩阵;如果参数为 [M,N] 可以省略掉方括号。例如:
%注:上述语句生成的随机数所服从的正态分布都是均值为 2,标准差为 3.
通过下面代码,可以生成大量随机数,查看大致的分布情况:
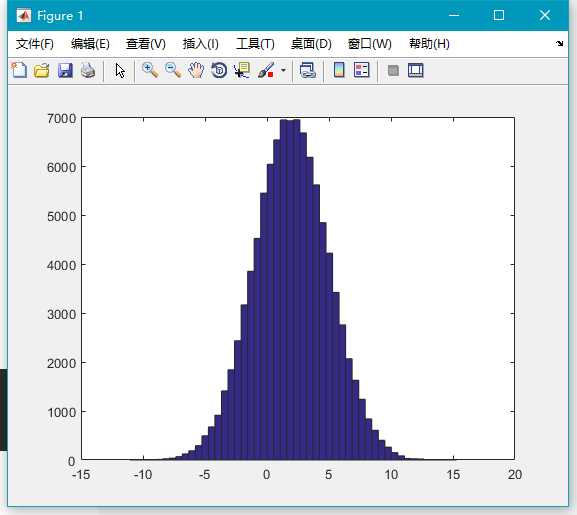
x=normrnd(2,3,100000,1);
hist(x,50);如图,上半部分是由上一行语句生成的均值为 2,标准差为 3 的 10 万个随机数的大致分布,下半部分是用小节 “randn()” 中最后那段语句生成 10 万个标准正态分布随机数的大致分布。
注意到上半个图像的对称轴向正方向偏移(准确说移动到 x=2 处),这是由于均值为2的结果。
而且,由于标准差是 3,比标准正态分布的标准差(1)要高,所以上半部分图形更胖 (注意 x 轴刻度的不同)。
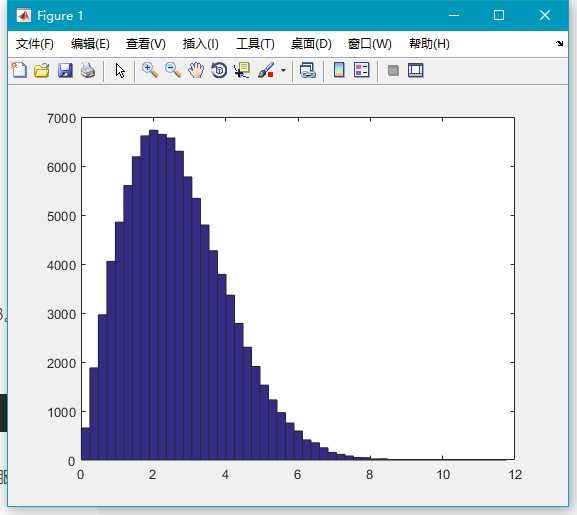
5.chi2rnd()
此函数生成服从卡方(Chi-square) 分布的随机数。卡方分布只有一个参数:自由度 v。基本语法
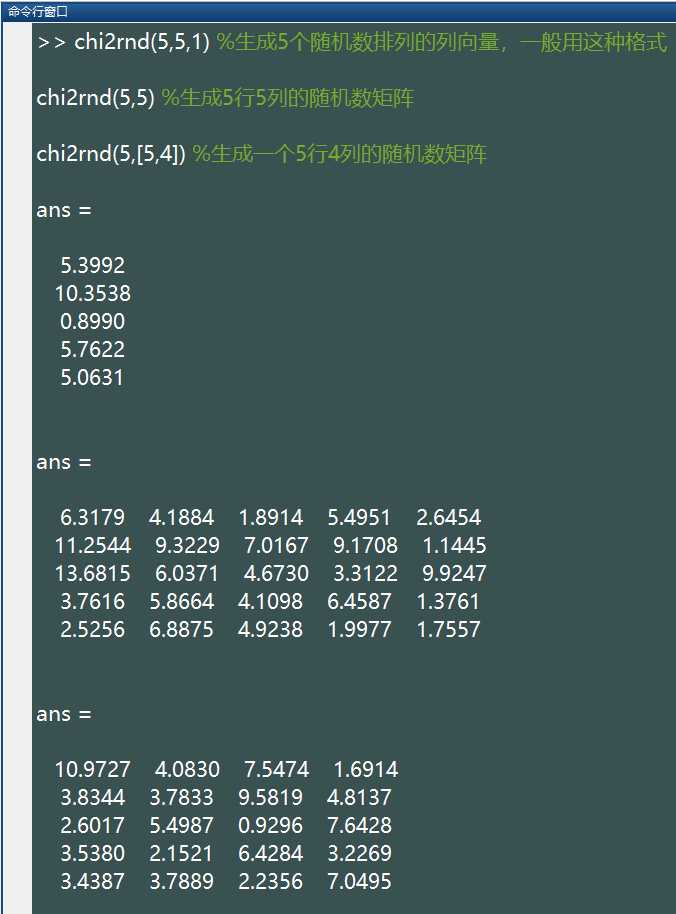
chi2rnd(v,[M,N,P,...])生成的随机数服从自由度为 v 的卡方分布,这些随机数排列成 M*N*P… 多维向量。如果只写 M,则生成 M*M 矩阵;如果参数为 [M,N] 可以省略掉方括号。例如:
%注:上述语句生成的随机数所服从的卡方分布的自由度都是5
通过下面代码,可以生成大量随机数,查看大致的分布情况:
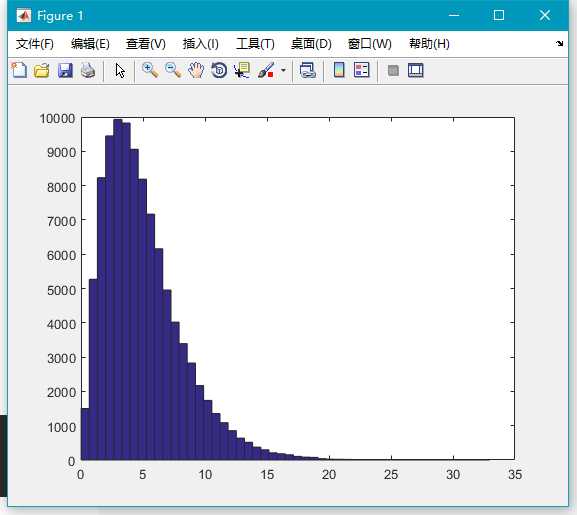
x=chi2rnd(5,100000,1);
hist(x,50);6.frnd()
此函数生成服从 F 分布的随机数。F分布有2个参数:v1, v2。基本语法
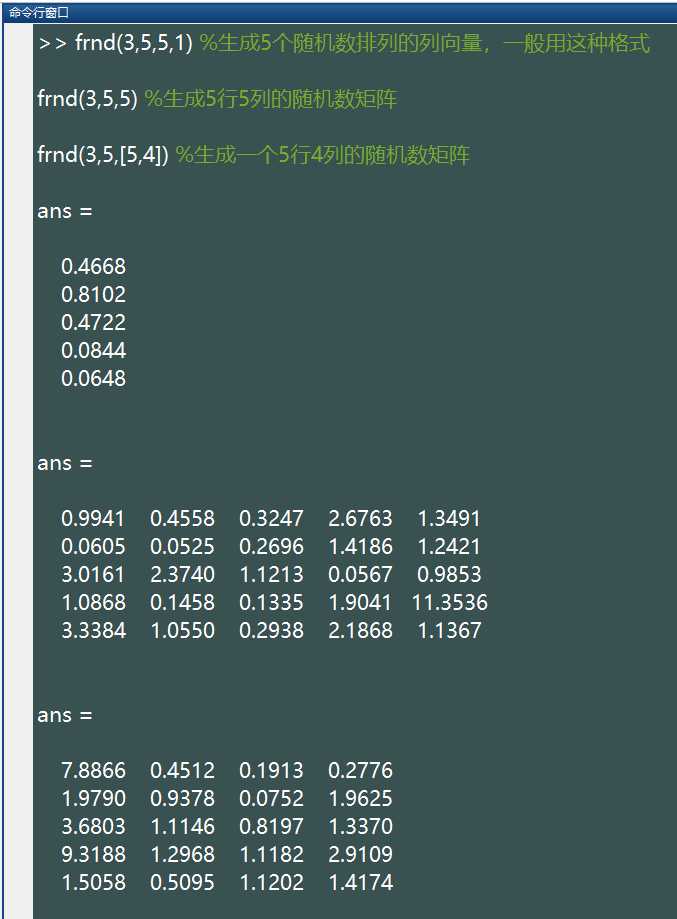
frnd(v1,v2,[M,N,P,...])生成的随机数服从参数为 (v1,v2) 的卡方分布,这些随机数排列成 M*N*P… 多维向量。如果只写 M,则生成 M*M 矩阵;如果参数为 [M,N] 可以省略掉方括号。例如:
%注:上述语句生成的随机数所服从的参数为 (v1=3,v2=5) 的 F 分布
通过下面代码,可以生成大量随机数,查看大致的分布情况:
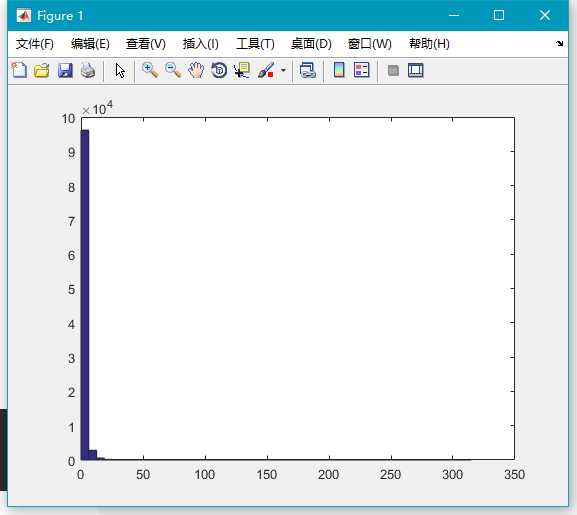
x=frnd(3,5,100000,1);
hist(x,50);从结果可以看出来, F分布集中在 x 正半轴的左侧,但是它在极端值处也很可能有一些取值。
7.trnd()
此函数生成服从 t 分布 (Student’s t Distribution,这里 Student 不是学生的意思,而是 Cosset.W.S. 的笔名) 的随机数。t 分布有 1 个参数:自由度 v。基本语法
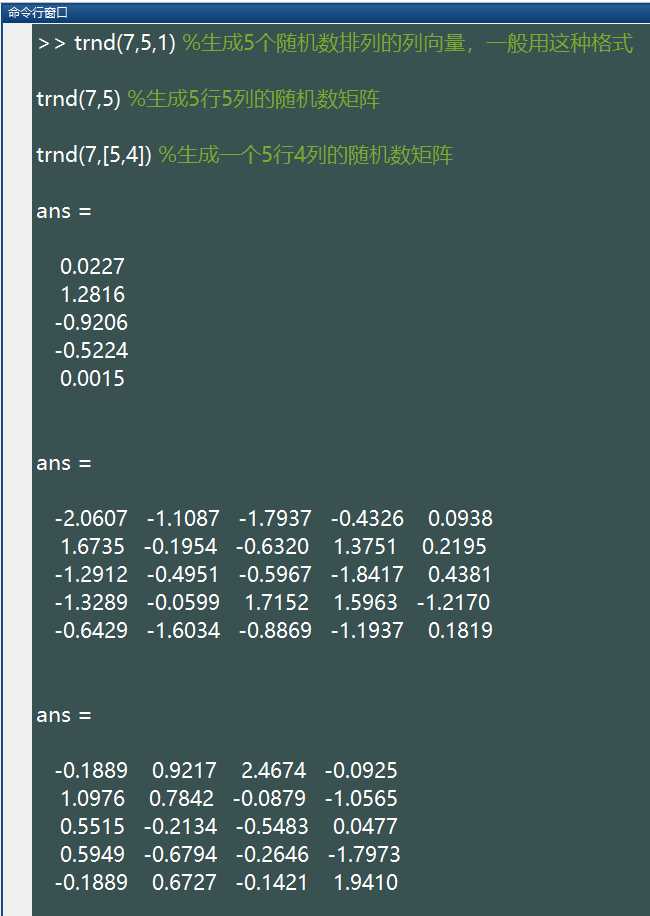
trnd(v,[M,N,P,...])生成的随机数服从参数为 v 的t分布,这些随机数排列成 M*N*P… 多维向量。如果只写 M,则生成 M*M 矩阵;如果参数为 [M,N] 可以省略掉方括号。例如:
%注:上述语句生成的随机数所服从的参数为 (v=7) 的 t 分布
通过下面代码,可以生成大量随机数,查看大致的分布情况:
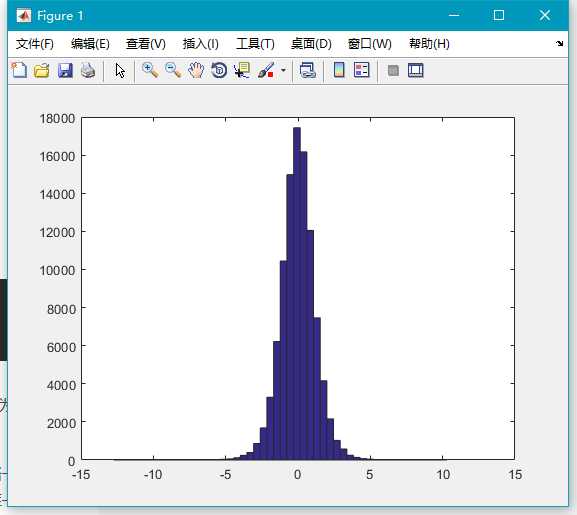
x=trnd(7,100000,1);
hist(x,50);可以发现t分布比标准正太分布要 “瘦”,不过随着自由度 v 的增大,t 分布会逐渐变胖,当自由度为正无穷时,它就变成标准正态分布了。
接下来的分布相对没有这么常用,同时这些函数的语法和前面函数语法相同,所以写得就简略一些。
8.betarnd()
此函数生成服从 Beta 分布的随机数。Beta 分布有两个参数分别是 A 和 B。
生成beta分布随机数的语法是:
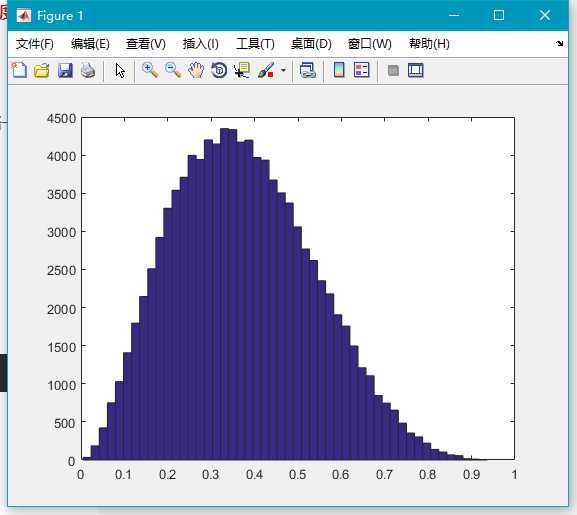
betarnd(A,B,[M,N,P,...])通过下面代码,可以生成大量随机数,查看大致的分布情况:
x=betarnd(3,5,100000,1);
hist(x,50);9.exprnd()
此函数生成服从指数分布的随机数。指数分布只有一个参数: mu。
生成指数分布随机数的语法是:
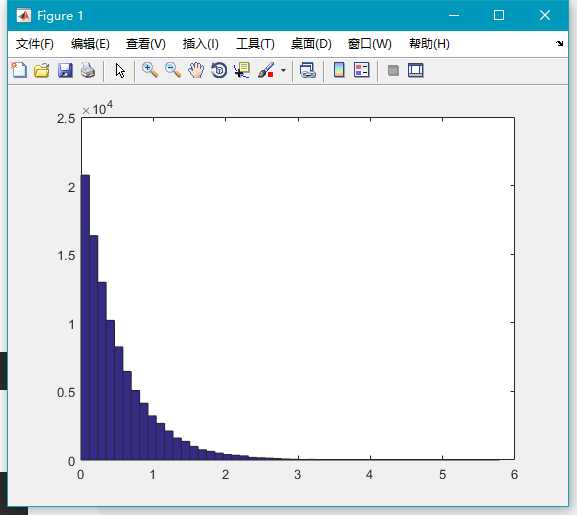
exprnd(mu,[M,N,P,...])通过下面代码,可以生成大量随机数,查看大致的分布情况:
x=exprnd(0.5,100000,1);
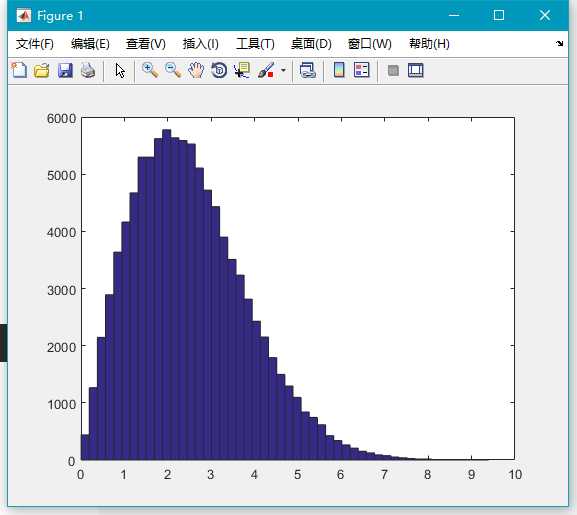
hist(x,50);10.gamrnd()
生成服从 Gamma 分布的随机数。Gamma 分布有两个参数:A 和 B。
生成 Gamma 分布随机数的语法是:
gamrnd(A,B,[M,N,P,...])通过下面代码,可以生成大量随机数,查看大致的分布情况:
x=gamrnd(3,5,100000,1);
hist(x,50);11.lognrnd()
生成服从对数正态分布的随机数。其有两个参数:mu 和 sigma,服从这个这样的随机数取对数后就服从均值为 mu,标准差为 sigma 的正态分布。
生成对数正态分布随机数的语法是:
lognrnd(mu,sigma,[M,N,P,...])通过下面代码,可以生成大量随机数,查看大致的分布情况:
x=lognrnd(-1,1/1.2,100000,1);
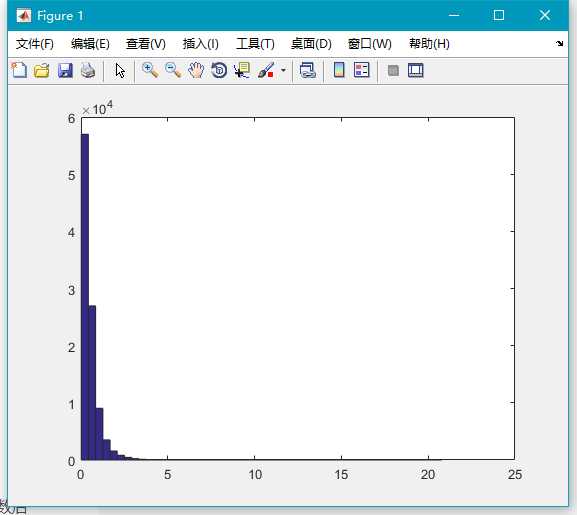
hist(x,50);12.raylrnd()
生成服从瑞利(Rayleigh)分布的随机数。其分布有 1 个参数:B。
生成瑞利分布随机数的语法是:
raylrnd(B,[M,N,P,...])通过下面代码,可以生成大量随机数,查看大致的分布情况:
x=raylrnd(2,100000,1);
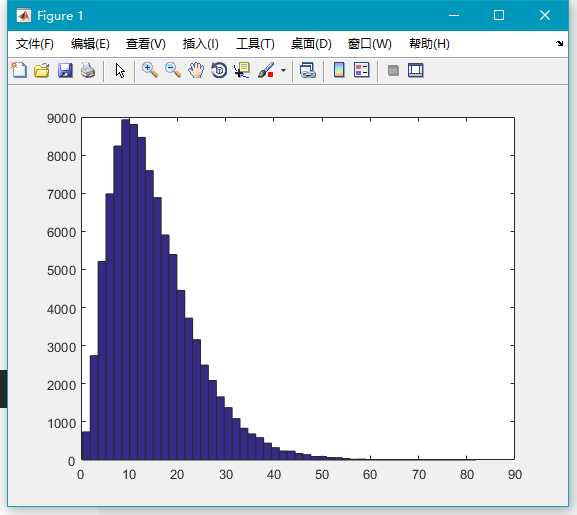
hist(x,50);13.wblrnd()
生成服从威布尔(Weibull)分布的随机数。其分布有 2 个参数:scale 参数 A 和 shape 参数 B。
生成 Weibull 分布随机数的语法是:
wblrnd(A,B,[M,N,P,...])还有非中心卡方分布(ncx2rnd),非中心F分布(ncfrnd),非中心t分布(nctrnd),括号中是生成服从这些分布的函数,具体用法用:help 函数名 的方法查找。
通过下面代码,可以生成大量随机数,查看大致的分布情况:
x=wblrnd(3,2,100000,1);
hist(x,50);c. 离散型分布随机数
离散分布的随机数可能的取值是离散的,一般是整数。
14.unidrnd()
此函数生成服从离散均匀分布的随机数。Unifrnd 是在某个区间内均匀选取实数(可为小数或整数),Unidrnd 是均匀选取整数随机数。离散均匀分布随机数有 1 个参数:n, 表示从 {1, 2, 3, … N} 这 n 个整数中以相同的概率抽样。基本语法:
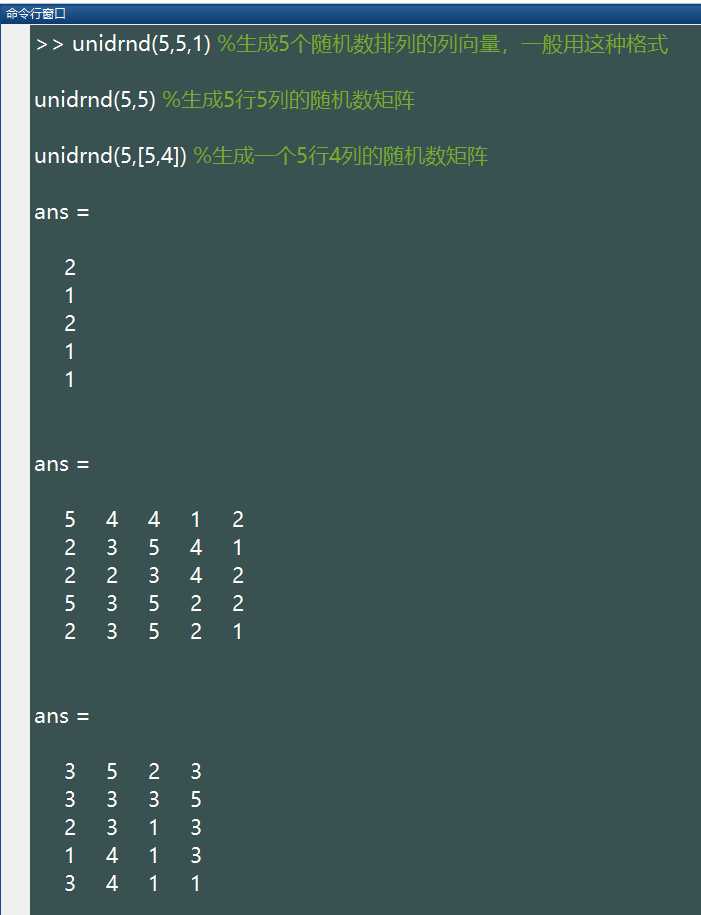
unidrnd(n,[M,N,P,...])这些随机数排列成 M*N*P… 多维向量。如果只写 M,则生成 M*M 矩阵;如果参数为 [M,N] 可以省略掉方括号。例如:
%注:上述语句生成的随机数所服从的参数为 (10,0.3) 的二项分布
通过下面代码,可以生成大量随机数,查看大致的分布情况:
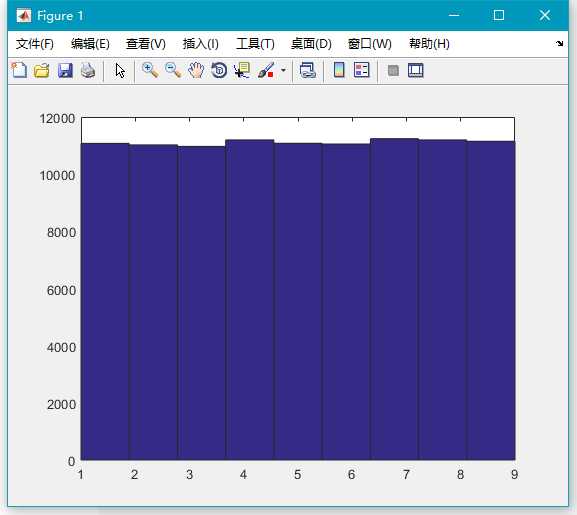
x=unidrnd(9,100000,1);
hist(x,9);可见,每个整数的取值可能性基本相同。
15.binornd()
此函数生成服从二项分布的随机数。二项分布有 2 个参数:n, p。考虑一个打靶的例子,每枪命中率为 p,共射击 N 枪,那么一共击中的次数就服从参数为(N,p)的二项分布。注意 p 要小于等于1 且非负,N 要为整数。基本语法:
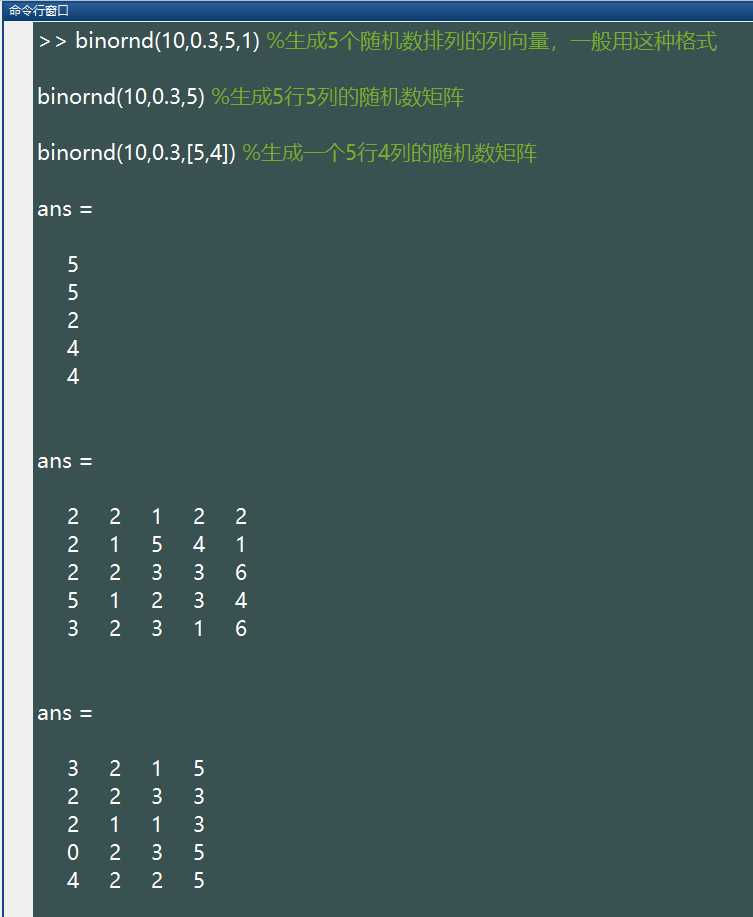
binornd(n,p,[M,N,P,...])生成的随机数服从参数为 (N,p) 的二项分布,这些随机数排列成 M*N*P… 多维向量。如果只写 M,则生成 M*M 矩阵;如果参数为 [M,N] 可以省略掉方括号。例如:
%注:上述语句生成的随机数所服从的参数为 (10,0.3) 的二项分布
通过下面代码,可以生成大量随机数,查看大致的分布情况:
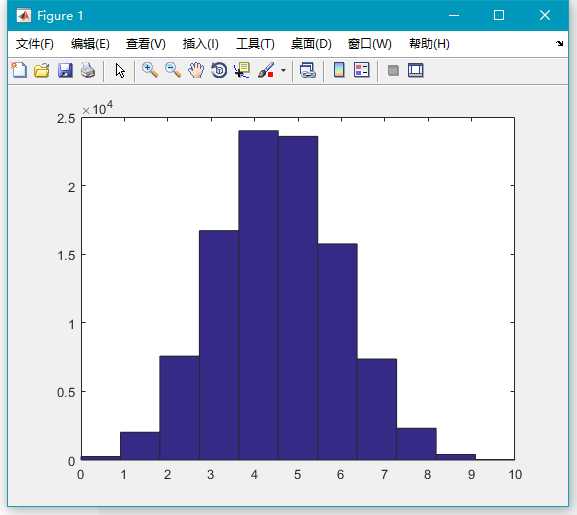
x=binornd(10,0.45,100000,1);
hist(x,11);我们可以将此直方图解释为,假设每枪射击命中率为 0.45,每论射击 10 次,共进行 10 万轮,这个图就表示这 10 万轮每轮命中成绩可能的一种情况。
16.geornd()
此函数生成服从几何分布的随机数。几何分布的参数只有一个:p。几何分布的现实意义可以解释为,打靶命中率为 p,不断地打靶,直到第一次命中目标时没有击中次数之和。注意 p 是概率,所以要小于等于1且非负。基本语法:
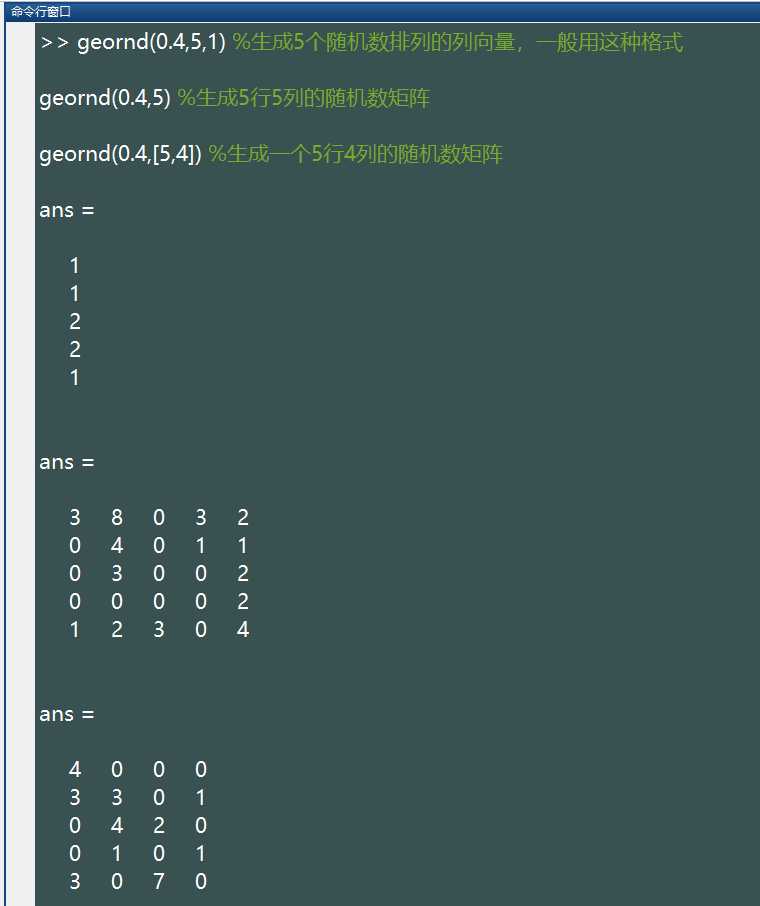
geornd(p,[M,N,P,...])这些随机数排列成 M*N*P… 多维向量。如果只写 M,则生成 M*M 矩阵;如果参数为 [M,N] 可以省略掉方括号。例如:
%注:上述语句生成的随机数所服从的参数为(0.4)的二项分布
通过下面代码,可以生成大量随机数,查看大致的分布情况:
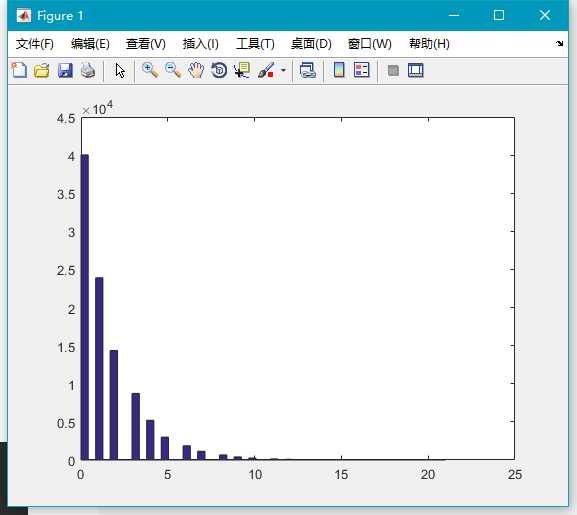
x=geornd(0.4,100000,1);
hist(x,50);17.poissrnd()
此函数生成服从泊松 (Poisson) 分布的随机数。泊松分布的参数只有一个:lambda。此参数要大于零。基本语法:
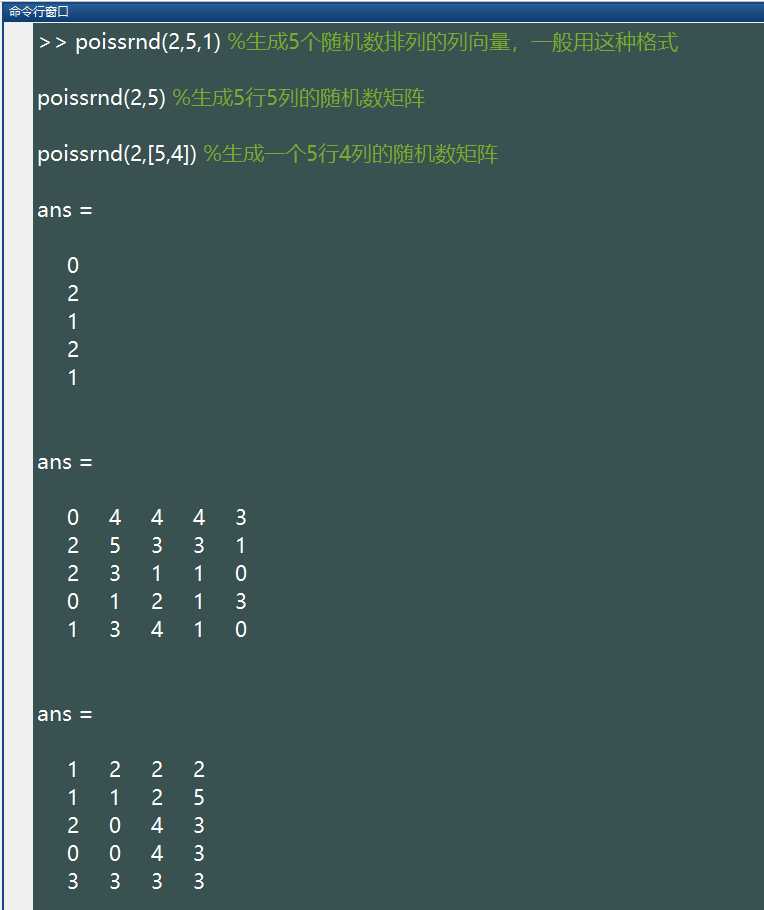
geornd(p,[M,N,P,...])这些随机数排列成 M*N*P… 多维向量。如果只写 M,则生成 M*M 矩阵;如果参数为 [M,N] 可以省略掉方括号。例如:
%注:上述语句生成的随机数所服从的参数为(2)的泊松分布
通过下面代码,可以生成大量随机数,查看大致的分布情况:
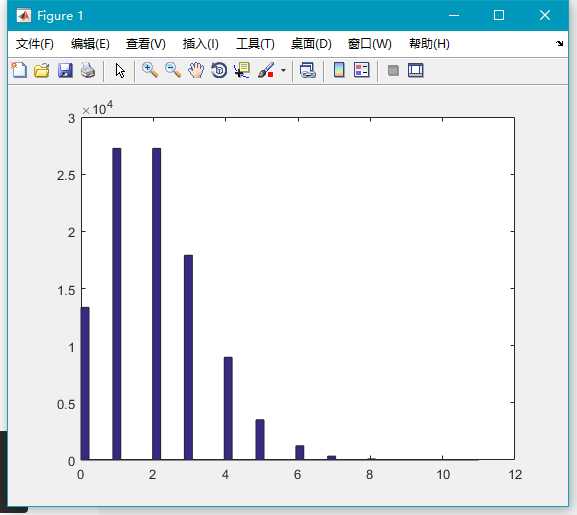
x=poissrnd(2,100000,1);
hist(x,50);其他离散分布还有超几何分布 (Hyper-geometric, 函数是 hygernd) 等,详细见 Matlab 帮助文档。
本博客文字大多来自博客 MATLAB随机数生成_MALSIS的博客-CSDN博客_matlab生成一个随机数
今天的文章MATLAB 生成随机数 方法总汇 (各分布配图参考)分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/13104.html