人工智能数学基础系列文章
人工智能的学习对于数学要求还是需要一定的功底的,不管是算法还是涉及到的名词概念,都是建立在数学模型的基础上来做训练学习的,所以非常有必要把涉及到的数学知识都理解和梳理一遍,才能把思维从传统的编程方式转变过来。
这里介绍的是 一元函数(标量场)的导数,以后会介绍多元函数(矢量或者多维矩阵场)导数,因为多元函数需要向量和矩阵相关的知识,会先介绍向量和矩阵相关之后,再来详细介绍多元函数导数问题
一、导数
1. 定义
函数导数f'(x0),就是函数f(x)在x0值处的导数,也是函数f(x)在x0这个点的切线斜率,这个点我们这里用P点表示,如图:
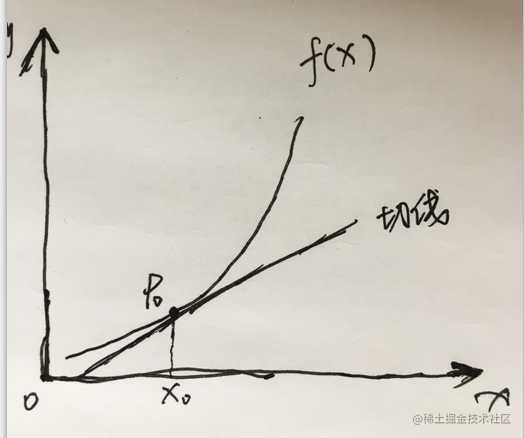
2. 求导的推导过程
我们知道高中的时候对于函数斜率的计算公式:y-y0 = m(x – x0),其中m就是函数的斜率。具体我们要怎么求出这斜率值或者导数呢。
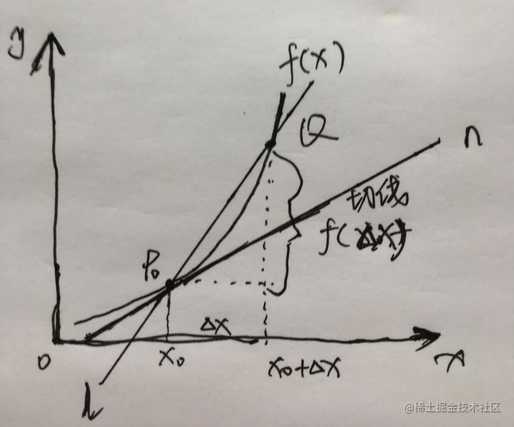
上图中,假设有一条直线l,与函数f(x)相交于p0和Q点,保持p0点不变,当Q点沿着函数f(x)向p0点无限靠近,P0点和Q点重合的时候,此时直线l就和P0的切线n重合,这是一个极限的无限趋于x0值(也就是P0点)的求解过程。 上图看出,P0点到Q点在x轴上的变化量是Δx,Q点的x值就是x0+Δx,Q点在y轴上的变化量就是Δy,或者叫Δf。
P0和Q点的坐标是: P0( x0, f(x0) ),Q( x0+Δx, f(x0+Δx) ) 最开始我们提到了,斜率的计算公式y-y0 = m(x-x0),m = (y – y0) / (x – x0),m = Δf / Δx, 这是割线l的斜率,要求P0的斜率,则要引入极限的概念,斜率或者说导数的如下(当Δx趋近于0的时候,也就是变化量趋于0的时候,Q点和P0点重合):
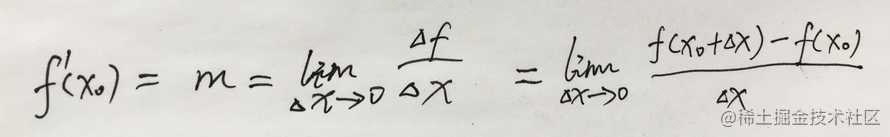
3. 求导例子
例子一
根据以上公式,举个例子,有函数f(x) = 1/x,求在x0上的导数?
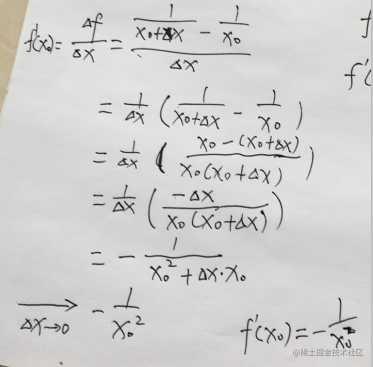
当Δx趋近于0的时候,函数1/x的导数是 -1/x^2。
例子二
函数1/x的导数求出来后,我们来解决一个有趣的问题,求出经过在函数f(x) = 1/x的点P的切线与坐标轴交点所围成的三角形的面积,如下图求出三角形AOB的面积:
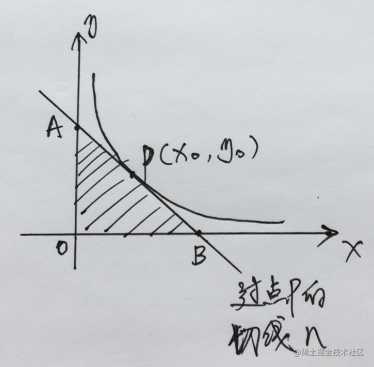
经过上面的学习,我们已经知道切线的方程:y-y0 = m(x – x0),函数f(x) = 1/x的导数是 -1/x^2,求三角形面积,我们只要求出线段AO和BO的长度,即在A点的坐标(0, y)和B点的坐标(x, 0),将A、B两点的坐标值和函数导数代入切线方程中得到:

求解的过程写的有点乱,将A、B坐标和导数代入后,求出A和B代表的三角形的两个边的y、x值。最后根据三角形面积公式:1/2
AOBO,求出面积为:2, 函数f(x) = 1 / x,比较神奇,过函数的点的切线与坐标轴交点所围成的三角形面积都是2。
例子三
既然函数f(x) = 1/x(即x的-1次幂)可以求其导数,f(x) = x^n,也可以求其导数,如下是求导过程:
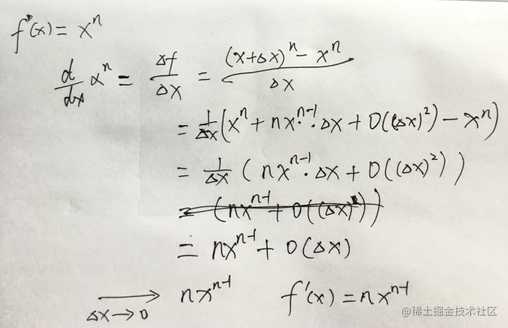
这里最难的是二项式(x + Δx)^n的展开为多项式,(二项式定理)这个高中的数学书应该有提及,其实只要试试(x + Δx)^2和(x + Δx)^3的展开,就可以找出其中规律,上图写的O((Δx)^2)是许多由Δx所组成的项式,因为我们求导最终是一个极限的过程,所以只有变化量的项式就写成了一个统称,没有实际的计算意义。最终得出当Δx趋于0的时候,函数f(x) = x^n的导数是 f ‘(x) = nx^n-1,通过这个导数公式也可以反过来证明我们上门例子一中所计算出的函数f(x) = 1/x的导数,也是f ‘(x) = -1/x^2(即-x^-2)。 经过例子三的计算,很容易对多项式函数进行求导,比如:f(x) = 10x^3 -2x^5,f ‘(x) = 30x^2 – 10x^4。
例子四
下面来推导下三角函数的导数: f(x) = sinx,f ‘(x) = (sinx)’,利用上门的求导公式,解得:
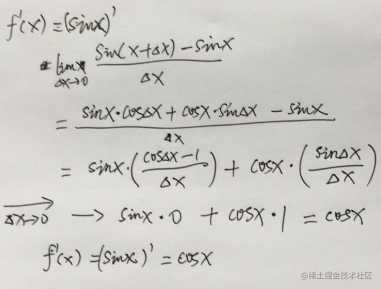
正弦的两角和公式展开后,求得Δx趋于0的时候,cosΔx等于1,所以cosΔx-1 / Δx等于0,Δx趋于0的时候,sinΔx等于0, sinΔx/Δx等于1。
余弦函数f(x) =cosx的求导,f ‘(x) = (cosx)’:
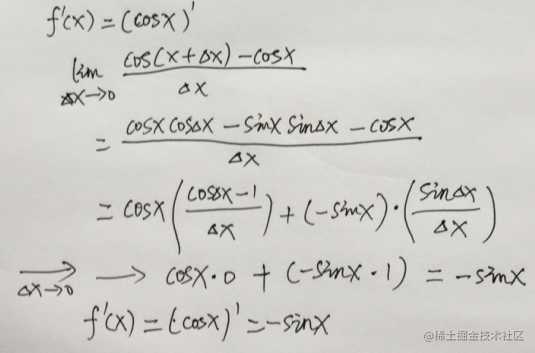
以上三角函数的两角和公式: sin(x + Δx) = sinx·cosΔx + cosx·sinΔx cos(x + Δx) = cosx·cosΔx – sinx·sinΔx
二、高阶导数
所谓高阶导数就是,函数的一次求导叫一阶导数,对一阶导数再次求导叫二阶导数,对二阶导数再次求导叫三阶导数,对三阶导数再次求导叫四阶导数,如果求导n次就是n阶导数,这些都是高阶导数。这里举个例子,函数f(x) = x^n,的n次导数,求解? 牛顿用f ‘(x)表示一阶导数,莱布尼茨在微分中使用 d/dx(x^n)来表示一阶导数也可以用D x^n 来表示,(d/dx)d/dx(x^n)表示二阶导数也可以用D ^2 x^n表示,n次导数可以用 D^n x^n
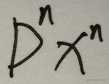
下面我们来对函数f(x) = x^n,进行n阶导求解:
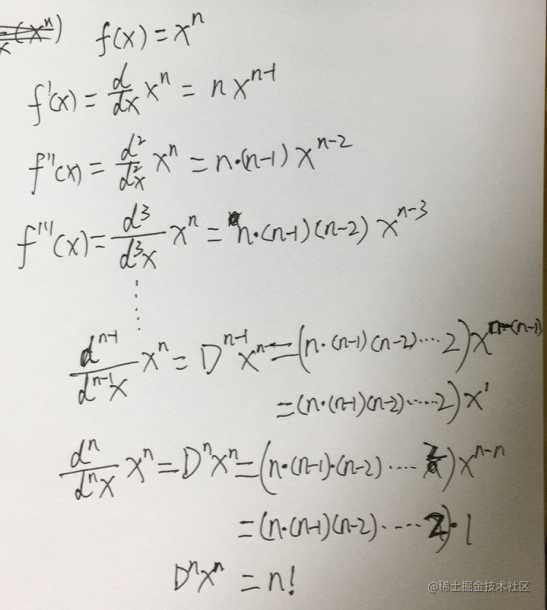
最终是一个n!,n的阶层是一个常量了,如果进行n+1次求导,那么函数f(x) = x^n的n+1阶导数就是0。
三、常用导数公式

其中指数和对数的会比较难记住,我就是经常记不住。o_o|||,惭愧高中指数和对数的知识也忘了。以后还是有必要专门有一篇是介绍和复习指数对数相关概念、性质和运算法则的文章。
导数知识先介绍到这,关于四则运算的求导,网上已有很多资料,可以上网查找其相关求导法则,万变不离其宗推导方式都可以利用第二小标题的“求导公式”来计算推导。希望这篇文章能对你有所帮助,回忆起高中导数和微分相关的内容。
人工智能数学基础系列文章
今天的文章人工智能数学基础—-导数分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/14741.html
