深度优先遍历 (DFS) 与广度优先遍历 (BFS)

前端小兵，不吝赐教

背景

看了很多前辈的分享后，笔者今天想整理下所理解的图的遍历算法。

图的遍历算法分为深度优先遍历与广度优先遍历，这两种算法从字面上了解的话，可以很清楚的知道。 一种是以深度，不断去查找是否有下级节点，如果有就继续递归向下查找，否则回到上级，再由未遍历的下级节点进入。 另一种是以广度，从一个节点，查找出它的所有子节点，再依次从所有子节点中向下查找所有子节点。

这是笔者对深度与广度优先遍历的浅面层次的看法。接下来，就进行详细的分析与理解。

深度优先遍历 (DFS)

深度优先遍历的思想可以分为以下几步：

1. 指定一点为顶点，进行标记，并查找该节点的任意一个相邻节点。

2. 若该相邻节点未被访问，则对其进行标记，并进入递归，查找它的未被标记访问的邻接节点；若该节点已被访问标记，则回退到上级节点，查找它未被标记访问的邻接节点，再进入递归，直到与起点相通的全部顶点都被标记访问为止。

3. 若所有节点都被标记访问，就结束；反之，如果还有节点未被访问，则需要以该节点为顶点进行下一步的递归查找，直到所有点都被标记访问。

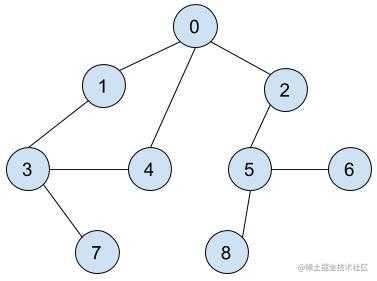
首先会先选择一个节点作为顶点，这里我们就以 0 为起点，然后进行标记，并查找该节点的任意一个相邻节点。

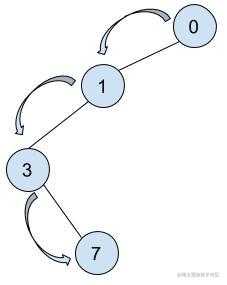
若该相邻节点未被访问，则对其进行标记，并进入递归，查找它的未被标记访问的邻接节点

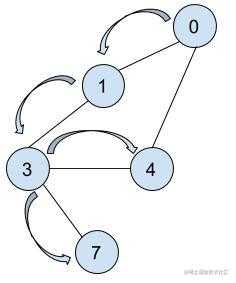
因为节点 4 的邻接节点 3 与 0 已被访问，则回退到节点 0 ，再进入下次递归，直到与起点相通的全部顶点都被标记访问为止

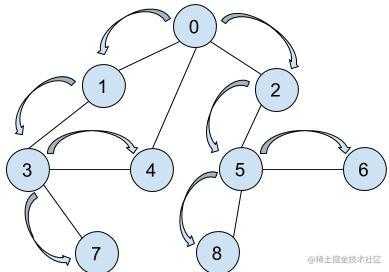
以上所有顶点都被访问标记，这次遍历就结束了，如果还有未被访问的，就说明未被访问的节点没有与节点 0 相通，是独立于这个通路的。 以上无向图的访问顺序为：v0, v1, v3, v7, v4, v2, v5, v8, v6（不唯一）

广度优先遍历 (BFS)

广度优先遍历，又称为”宽度优先搜索”或”横向优先搜索”，简称 BFS。它的实现思想是：从一点出发，查出它的邻接节点放入队列并标记，然后从队列中弹出第一个节点，寻找它的邻接未被访问的节点放入队列，直至所有已被访问的节点的邻接点都被访问过；若图中还有未被访问的点，则另选一个未被访问的点出发，执行相同的操作，直至图中所有节点都被访问。

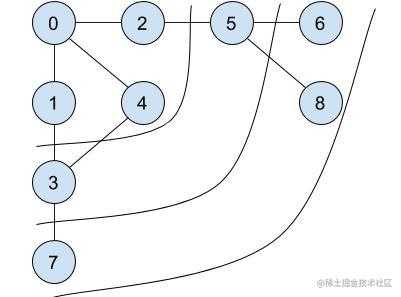
由近到远的访问方式，步骤是：

1. 创建一个队列，并将开始节点放入队列中

2. 若队列非空，则从队列中取出第一个节点，检测它是否为目标节点

   • 若是目标节点，则结束搜寻，并返回结果
   • 若不是，则将它所有没有被检测过的子节点都加入队列中

3. 若队列为空，表示图中并没有目标节点，则结束遍历

以上图中，没有设置目标节点，所以遍历所有节点。 先访问节点 0 ，依次访问了节点 1，4，2，接着访问节点 3，5，最后再访问 7，8，6，因此它的访问顺序是：v0, v1, v4, v2, v3, v5, v7, v8, v6（不唯一）

创建图：

const vertices = []; // 图的顶点集合
const edges = new Map(); // 图的边集合

/**
 * 添加节点
 **/
addVertex = (v: string) => {
  this.vertices.push(v);
  this.edges.set(v, []);
};

/**
 * 添加边
 **/
addEdge = (v: string, w: string) => {
  const vEdge = edges.get(v);
  vEdge.push(w);
  const wEdge = edges.get(w);
  wEdge.push(v);
  edges.set(v, vEdge);
  edges.set(w, wEdge);
};

formatToString = () => {
  let s = "";
  vertices.forEach(v => {
    s += `${v} -> `;
    const neighors = edges.get(v);
    neighors.forEach(n => (s += `${n} `));
    s += "\n";
  });
  return s;
};

深搜：

graphDFS = () => {
  const marked = [];
  vertices.forEach(v => {
    if (!marked[v]) {
      dfsVisit(v);
    }
  });

  const dfsVisit = (u: string) => {
    marked[u] = true;
    const neighbors = edges.get(u);
    neighors.forEach(n => {
      if (!marked[n]) {
        dfsVisit(n);
      }
    });
  };
};

广搜：

graphBFS = (v: string, t?: string) => {
  const queue = [],
    marked = [];
  marked[v] = true;
  queue.push(v); // 添加到队尾
  while (queue.length > 0) {
    const s = queue.shift(); // 从队首移除
    if (t && s === t) {
      console.log("target vertex: ", t);
      return;
    } else if (edges.has(s)) {
      console.log("visited vertex: ", s);
    }
    const neighbors = edges.get(s);
    neighors.forEach(n => {
      if (!marked[n]) {
        marked[n] = true;
        queue.push(n);
      }
    });
  }
};

总结

今天整理了下自己所理解的深度优先遍历与广度优先遍历的思想及实现，感谢各位的观看，谢谢！

站在巨人的肩膀

深度优先遍历与广度优先遍历