如何生成指定分布的随机数

前言

对于随机数平时我们还是比较常用的，一般都会直接通过各种语言原生自带的随机函数，比如 c++ 中有random()函数，java 中有 Random 类，python 有 random 模块等等。都能很方便生成随机变量，但它们有一个特点，那就是都服从均匀分布，而有些场景需要要生成不同分布的随机变量。

随机变量

随机变量即随机函数，通过该函数能生成每个可能事件对应的一个值。比如我们掷骰子，每次按一定的概率生成一个值。有两种类型变量，

离散型随机变量，能取到的不相同的值是有限个或可列无限多个。
连续型随机变量，能取到的值可以是连续的，在某个区间内可取任意一实数。

概率密度函数

主要用来表示不同点对应的概率大小，即X轴上每个单位长度对应的概率大小。概率等于面积，当某区间长度趋于0时则变为一个点，此时概率大小为f(x)。

常见分布

伯努利分布，即0-1分布，随机变量为0或为1，概率为p和1-p。
二项分布，进行n次伯努利实验，相对于不同成功次数对应的概率。
泊松分布，是二项分布的极限形式。
均匀分布，在相同长度间隔的分布概率是等可能的。
正态分布，又名高斯分布，正态曲线呈钟型，两头低，中间高。
指数分布，描述事件以恒定平均速率连续且独立地发生的过程的概率分布。
逻辑斯蒂分布，增长分布，形状有点像正态分布。

生成分布算法

Inverse Transform Method，首先生成一个均匀分布的随机数，再求指定分布的分布函数F(x)，然后求得F(x)的逆函数G(x)，将随机数带入逆函数得到的即为指定分布的随机数。
Acceptance-Rejection Method，首先生成一个均匀分布随机数a，设概率密度函数为f(x)，然后再生成一个均匀分布随机数b，若b<=f(a)，则成功得到指定分布的随机数，否则从头开始。

实现

两种算法都比较容易理解，第一个需要求逆函数，有时并不好求，而第二个基本没什么限制，对于任何分布都能很完成任务。下面就用第二种方法实现生成几种分布的随机数。

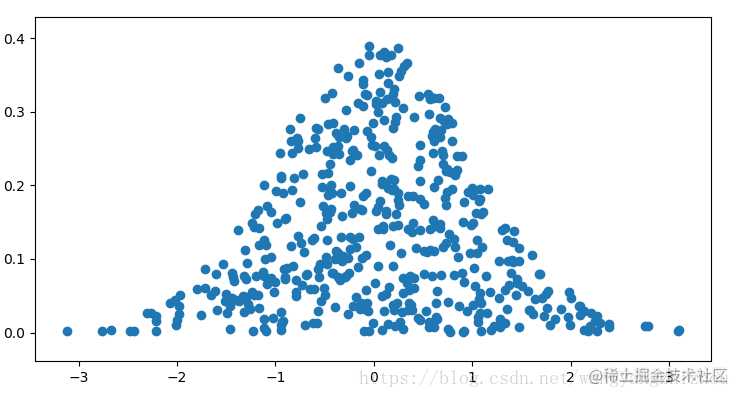
正态分布

def normal_pdf(x, mu=0, sigma=1):
    return (1 / (math.sqrt(2 * math.pi) * sigma)) * (math.exp(-math.pow(x - mu, 2) / (2 * math.pow(sigma, 2))))
    
def standard_normal_rand():
    while True:
        a = random.uniform(-4.0, 4.0)
        b = random.uniform(0.0, 3.0)
        if b < normal_pdf(a):
            return a, b

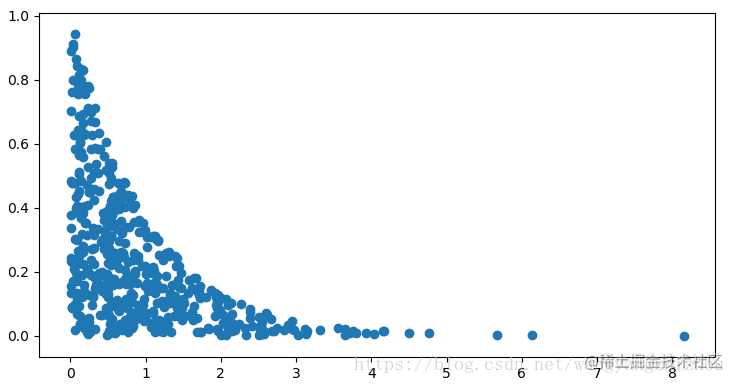
指数分布

def exponential_pdf(x, lam=1):
    return lam * math.exp(-lam * x)
    
def exponential_rand():
    while True:
        a = random.uniform(0.0, 100.0)
        b = random.uniform(0.0, 3.0)
        if b <= exponential_pdf(a):
            return a, b

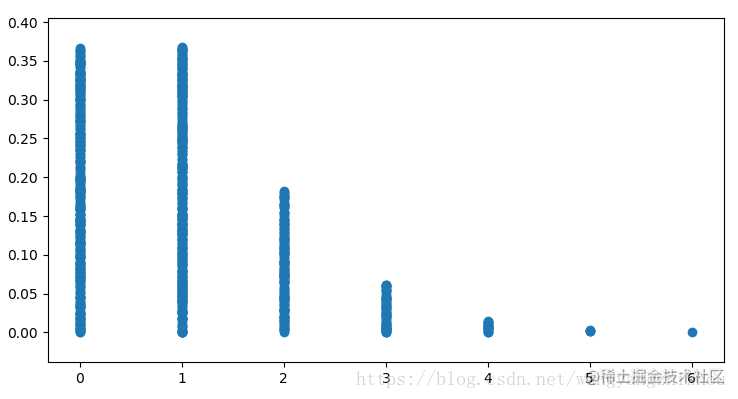
泊松分布

def poisson_pdf(x, lam=1):
    return (math.pow(lam, x) / math.factorial(x)) * math.exp(-lam)

def poisson_rand():
    while True:
        a = random.randint(0, 50)
        b = random.uniform(0.0, 1.0)
        if b <= poisson_pdf(a):
            return a, b