ECMAScript中的Number Type与 IEEE 754-2008

introduction

稍微深入了解一下JavaScript浮点数的开发者都会知道浮点数的误差问题，也就是说IEEE754-2008的浮点数误差。 常见的案例为: 0.1 + 0.2 = 0.30000000000000004 无论是google一下或者baidu一下，这类文章层出不穷，但是很多都是浅尝即止，无法让我能够逻辑通顺的理解。在所有阅读的中文资料当中，我觉得较优秀的是camsong同学的抓住数据的尾巴，有些图是直接借鉴该同学的(会注明)，但是这篇文章的一个问题是，对于某些数学上的区间表示不清楚，比如究竟是开区间还是闭区间。因此，我写下了该篇文章。 主要阅读的资料来源: ECMAScript 2015, ECMAScript 2018, wiki, etc.

首先，给出大家整篇内容的思维导图:

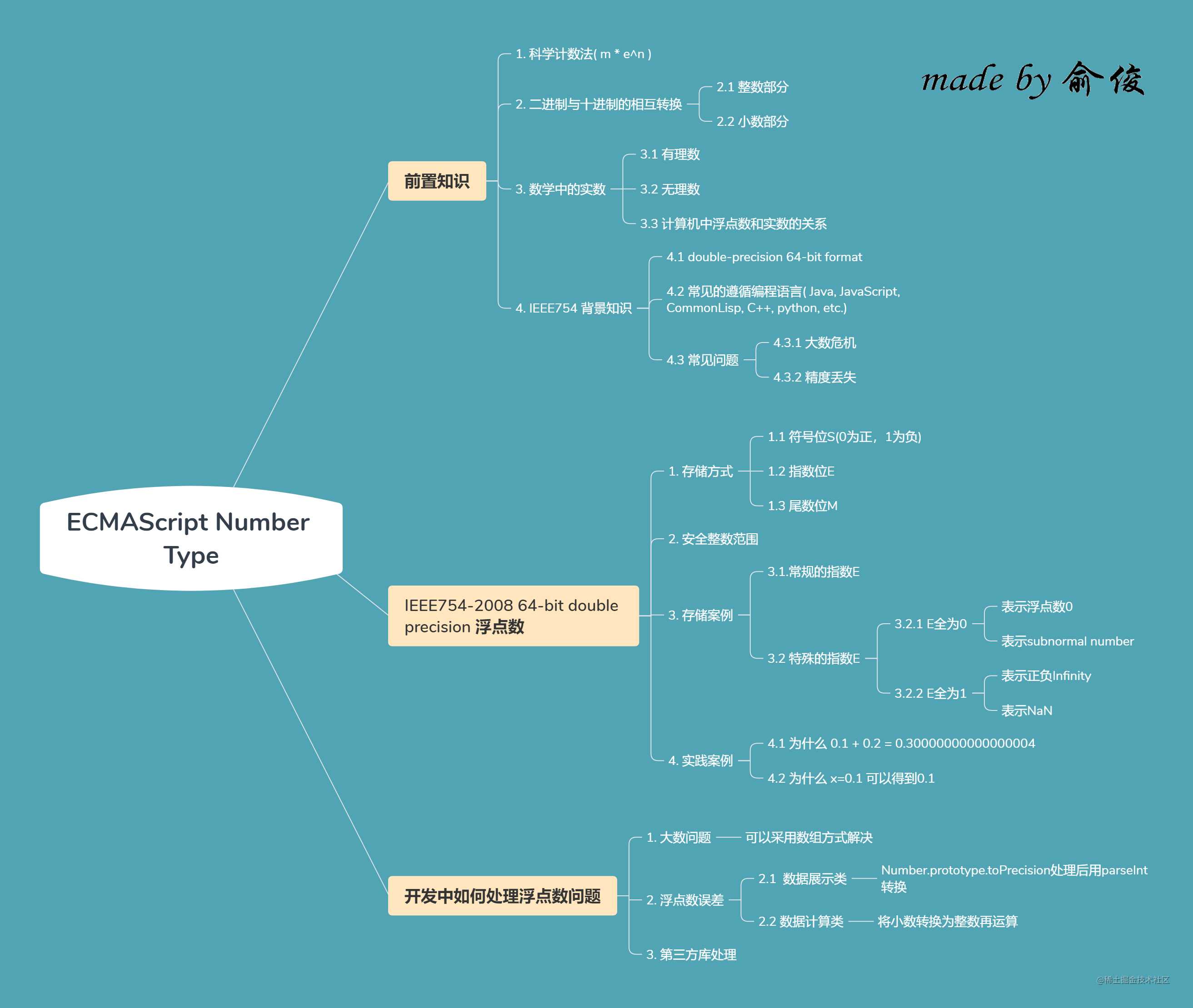
前置知识

1. 代数数学告诉我们实数(real number)包含有理数(rational number)和无理数:

• 有理数是一个整数a和一个正整数b的比(a/b),是整数和分数的集合，整数可以看成分母为1的分数，有理数的小数部分是有限的或为无限循环的数。
• 无理数是所有不是有理数字的实数，常见的无理数有：欧拉数e，黄金比例φ,数字π等.

很明显，在后面会知道，现代计算机使用有限的bits来存储浮点数，因此只能精确的表示实数中小数部分为有限的有理数，对于其他的数学实数数字只能是近似等于而已。借用网络上的一张图表示即是：

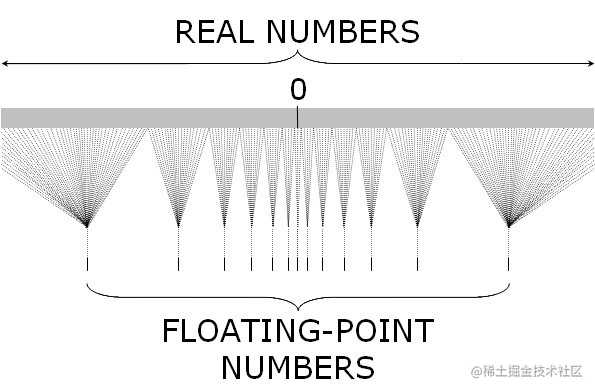
结论1：数学中的实数是连续的直线，而计算机中浮点数是实数直线的间断的点。

2. 在1985年以前，编程语言对于浮点数的存储各自有各自的标准，而在1985年后，基本都采用IEEE754 arithmetic标准，目前IEEE754最新版本为IEEE754-2008, 而ECMAScript 2015以后Number Type遵循 double-precision 64-bit format IEEE754-2008 arithmetic. 具体的章节为 6.1.6 The Number Type

需要注意的是，任何标准的实现可能和标准本身有差别，而ECMAScript Number Type在描述Number type和IEEE754-2008在对double-precision 64-bit format的描述有稍微的不同, 具体在后面详细讲解

3. 遵循IEEE-754的常见语言实现，比如 C and C++, Common Lisp, Java, JavaScript等。这类语言常见的关于小数的问题有两类：

• 数据精度丢失
• 大数危机(安全整数范围)

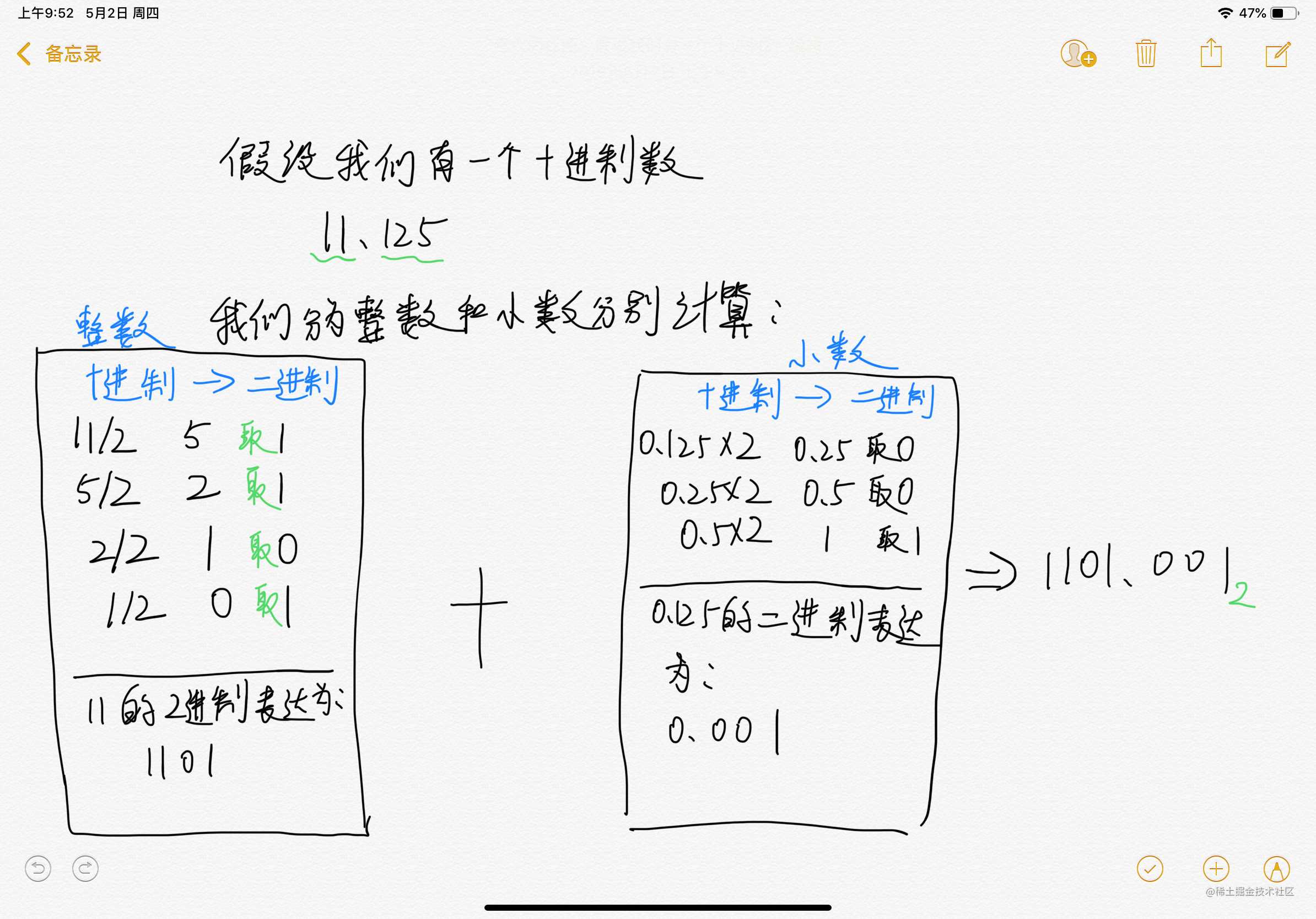
4. 我们回顾一下计算机组成原理当中，关于二进制和十进制的转换,主要分为整数部分和小数部分：

IEEE754 64-bit double precision 浮点数

首先看下浮点数的存储方式，64bits可以分为3个部分：

• 符号位S： 第一位是正负数符号位(sign), 0表示正数，1表示负数。这也是为什么会出现+0和-0的原因。
• 指数位E：中间的11位存储指数(exponent），用来表示次方数
• 尾数位M：最后的52位是尾数(mantissa), 超出的部分采用进1舍0.

采用wiki上的图表示就是:

转换成数学公式为:

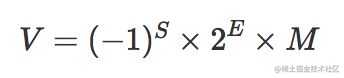
1. 上述的公式很明显遵循科学计数法的规范，十进制0<M<10,二进制位0<M<2，也就是对于二进制来讲整数部分只能是1，所以为了更高的精度表示,我们在计算机中存储的时候可以舍去整数部分的1，只保留后面的小数部分。

11.125 转换成二进制为 1101.001 转换成科学表达式  1.101001* 2^3

2. 我们来看指数位E，E是一个无符号整数，取值范围是[0, 2047]，但是我们通常用科学计数法表示数据时指数是可以为负数的，因此约定一个中间数(exponent bias)1023表示为0，因此[1,1022]表示指数位负，[1024,2046]表示为正(这里注意指数位为0和2047被用作特殊数字用途)。最后的公式变化为:

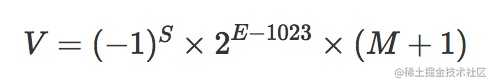
3. 下面我们用0.1来解释浮点误差的原因：

• 0.1转成二进制表示为0.0001100110011001100(1100循环), 转成科学计数法为1.100110011001100 * 2^-4,因此E= -4+1023 = 1019;M舍去舍去首位的1，小数点后第53位为1，遵循进1舍0，得到最后的结果为:

我们将上面的二进制数字在数学上转化成十进制为: 0.100000000000000005551115123126, 即出现了经典的浮点数误差.

4. 下面我们来看看M，也就是精度。53-bit significand precision转换成10进制能够保证15到17位的significant decimal digits precision（2−53 ≈ 1.11 × 10−16）， IEE754-2008对于边界情况有如下：

• 如果一个十进制有最多15个有效数字，转换成IEEE double-precision表示，然后再转换成十进制，最后的结果必须和最开始的十进制相同
• 如果一个IEEE 754 double-precision数字转换成一个十进制(至少17 significant digits)，然后再转换成double-precision 表示，最后的结果也必须和最开始的二进制相同。

因此，53-bit的精度转换成10进制为16个十进制数字(53log10(2) 约等于15.955).

安全整数

首先，我们给出结论，ECMAScript的安全整数范围为 [-2^53, 2^53]，那么为什么呢？

1. IEE754 64-bit无法表示2^53 + 1，因为尾数只有52位，共有2^53个选择，而2^53 + 1，转换成科学计数法 2^53 * (1+ 2^-53)，IEEE754 64-bit是没有办法表示的。这样明显是不安全的。

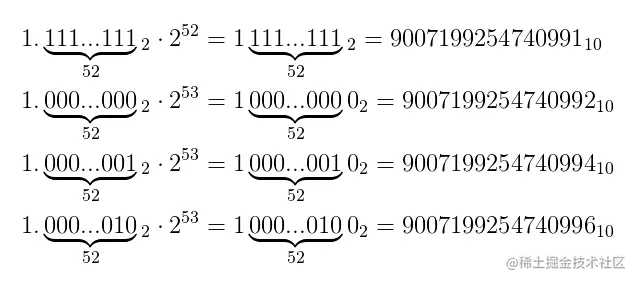
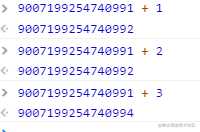
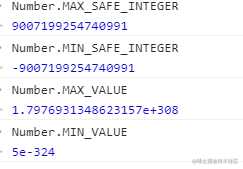
但是对于2^53 + 2，转换成科学计数法 2^54 * (1+ 2^-52)可以用IEEE754 64-bit表示。

2. 根据上面的现象，IEEE754能够表示的浮点数可以抽象为:

• [2^53, 2^54] 之间的数,IEEE754 64-bit能够表示的数都是可以被2整除的，两数之间的间隔为2.
• [2^54, 2^55] 之间的数的间隔为4
• 那么 [2^51, 2^52] 的数字与数字的间隔为0.5
• 数学归纳法总结一下:The spacing as a fraction of the numbers in the range from 2^n to 2^n+1 is 2^(n−52).

具体实现的64-bit precision案例

1. 这里可以看出指数E为0和2047是有特殊含义的，E为0除了表示+0和-0，还表示subnormal numbers. E为2047除了表示+Infinity和-Infinity，还表示各种NaN。NaN的个数为2^53 - 2个。

2. 引入了两个概念:subnormal double和normal double,下面的图基本能够表达两者之间的数学含义:

在计算机系统当中，一个未增强的floating-point system只能包含normalized numbers（上图中的红色），而允许subnormal numbers（蓝色）扩展了系统的数字范围，处于系统underflow gap（下溢）和0之间。下面用案例详细解释了两者之间的区别：

• 在normal floating-point value当中，我们通过exponent（指数）的偏移来移除尾数(significand)的0(比如0.0123 = 1.23 * 10^-2)。而subnormal numbers在significand中使用了leading zero，什么是leading zero具体看下面。
• 在IEEE floating-point number当中，比如一个positive normalized number，通常可以表示为m~0~.m~1~m~2~…m~p-1~（这里~2~表示的下标，m代表一个sidnificant digit, p是精度，m~0~不为0）。对于一个subnormal number, exponent是可能表示的最小的exponent，zero是significand digit （0.m~1~m~2~…m~p-1~），也就是说所有的subnormal number都比最小的normal number更接近0.

ECMASCript2015 specification: 6.1.6 Number Type

在ECMAScript规范当中，并没有直接用s * 2^(e-1023) * M这种表达方式，而是将M通过位移转换成整数，也就是s * 2 ^ (e-1075) * M. 这是需要注意的一点。 具体规范当中总结出来以下几点：

1. 64 bit去掉一位符号位，可以表达为 2^64 个不同的值，而IEEE754中2^53 – 2个 “not-a-number”值在ECMAScript中统一表达为NaN，也就是说，Number type有(2^64 – 2^53 + 3)个不同的values。
2. 两个特殊的值，为Infinity 和 -Infinity, 这里两个值的exponent转换为二进制位11个1，mantissia全为0(二进制).具体可以看上一小节的图篇案例。
3. 根据上面两点推断出，有2^64 – 2^53个finite numbers. 一半是positive numbers，另一半是negative numbers。也就是说这类值包含有positive zero和negative zero两个0值.
4. 也就是说，有2^64 – 2^53-2个非0的finite values，而这类值可以分为两类:
   • normalized value ：共包含2^64 – 2^54个值，这类值的form是: s * M * 2^e, s是+1或-1, m是positive integer（[2^52, 2^53)）,e的范围是[-1074, 951]，这里可以看出ECMAScript的实现没有采用exponent bias的表达方式

• denormalized number: 共有2^53 - 2个，公式仍然是: s * M * 2^e, s是+1或-1, m是positive integer（(0, 2^52)）,e的值为-1074

5. 我们知道，实际上按照二进制转十进制计算，由于E的最大值是1023(除了特殊的两个e取值)，也就是说实际上可以表示的最大整数位2^1024 - 1，我们知道这超过了最大安全整数范围。对于不能用IEEE-754 64-bit表示的值采取round to nearest, ties to even 的模式，round to nearest我们理解，但是什么是ties to even呢? 举个例子: 9007199254740995在IEEE754 64-bit中是无法表示的，因此会被绑定到9007199254740996上面去。

下面为什么0.1 + 0.2 = 0.30000000000000004?

我们来看计算步骤:

// 0.1 和 0.2 都转化成二进制后再进行运算
0.00011001100110011001100110011001100110011001100110011010 +
0.0011001100110011001100110011001100110011001100110011010 =
0.0100110011001100110011001100110011001100110011001100111

转换为IEEE754 double point为 1.0 0110 0110 0110 0110 0110 0110 0110 0110 0110 0110 0110 0110 100 * 2^(-2),如果用二进制转成十进制为(0.3 + 5/(100 * 2^50)).去小数点后面17位精度为0.30000000000000004，
这里取的是17位而不是16位，是IEEE754的规范中的计算结果

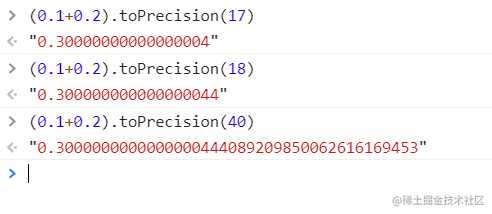
为什么x=0.1能得到0.1

在ECMAScript当中，没有使用IEEE754的exponent bias，而是把mantissa当中是整数，exponent为[-1024,951]，而2^53的十进制表示最多16位有效数字，也是最大表示的进度:

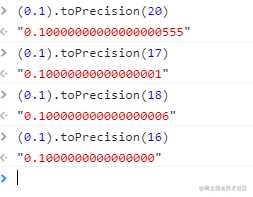
我们该如何处理这类浮点误差问题

首先，让我回想起在刷LeetCode题的时候，有一类问题即大数问题，当要计算的数超出了语言的上限，那时候我们是用数组来处理的。

首先引入两个方法, Number.prototype.toPrecision和Number.prototype.toFixed，两者都能够对于多余数字做凑整处理：

• toPrecision：The toPrecision() method returns a string representing the Number object to the specified precision，是用来处理精度的，对于精度数学中表示从左只右第一个不为0的数字开始算起
• toFixed: 从小数点后指定位数取整。

对于使用toFixed来做凑整处理，我们需要注意一些特殊案例: 比如(1.005).toFixed(2)返回1.00，因为1.005实际为1.0049999999999999999 而对于浮点误差问题，我们通常分成两类解决方案，解决方案来自camsong同学：

1. 对于数据展示类 对于需要展示的数字使用toPrecision处理后，用parseInt转成数字再显示:

function strip(num, precision = 12) {
  return +parseFloat(num.toPrecision(precision));
}

这里camsong同学采取12作为默认精度，是经验的选择，因为一般选12能处理大部分问题

2. 对于数据运算类 先将小数转成整数再运算:

/**
 * 精确加法
 */
function add(num1, num2) {
  const num1Digits = (num1.toString().split('.')[1] || '').length;
  const num2Digits = (num2.toString().split('.')[1] || '').length;
  const baseNum = Math.pow(10, Math.max(num1Digits, num2Digits));
  return (num1 * baseNum + num2 * baseNum) / baseNum;
} 

并且该同学也提供了相关地库:number-precision

一些其他著名的库包括但不限于: Math.js, big.js等

reference

1. IEEE754 double 可视化
2. 抓住数据的小尾巴 – JS浮点数陷阱及解法
3. double-precision floating-point format
4. denormal number
5. floating point arithemtic
6. What Every Computer Scientist Should Know About Floating-Point Arithmetic
7. ECMAScript Number Type