- 简单总结二叉树,二叉查找树,B树,B+树,红黑树
- 结合数据库中索引的存储,分析B树和B+树
Ref
二叉树
Overview
- 二叉树中,每个节点有不能多于2个的子节点。
- 二叉树常被用于实现二叉查找树和二叉堆。
- 一棵深度为
k,且有2^k-1个结点的二叉树,称为满二叉树。这种树的特点是每一层上的结点数都是最大结点数。 - 具有
n个结点的完全二叉树的深度为floor(log2n)+1。 - 深度为
k的完全二叉树,至少有2^(k-1)个叶子结点,至多有(2^k)-1个结点。
二叉树又包括如下类型
- 完全二叉树 —— 若设二叉树的高度为
h,除第h层外,其它各层 (1~h-1) 的结点数都达到最大个数,第h层有叶子结点,并且叶子结点都是从左到右依次排布,这就是完全二叉树。 - 满二叉树 —— 除了叶结点外,每一个结点都有左右子叶且叶子结点都处在最底层的二叉树。
- 平衡二叉树 —— 平衡二叉树又被称为
AVL树(区别于AVL算法),它是一棵二叉排序树,且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过 1,并且左右两个子树都是一棵平衡二叉树。
遍历二叉树
二叉树的遍历,有如下3种方式
- 先序遍历
- 中序遍历
- 后序遍历
此处给出一个结论,通过先序和中序,或者中序和后序,我们可以还原出原始的二叉树;但是通过先序和后序,是无法还原出原始的二叉树的。
- 先序遍历 代码实现
/** * 先序遍历 * @param rootTreeNode 根节点 */
public static void preTraverseBTree(TreeNode rootTreeNode) {
if (rootTreeNode != null) {
//访问根节点
System.out.println(rootTreeNode.getValue());
//访问左节点
preTraverseBTree(rootTreeNode.getLefTreeNode());
//访问右节点
preTraverseBTree(rootTreeNode.getRightNode());
}
}
- 中序遍历 代码实现
/** * 中序遍历 * @param rootTreeNode 根节点 */
public static void inTraverseBTree(TreeNode rootTreeNode) {
if (rootTreeNode != null) {
//访问左节点
inTraverseBTree(rootTreeNode.getLefTreeNode());
//访问根节点
System.out.println(rootTreeNode.getValue());
//访问右节点
inTraverseBTree(rootTreeNode.getRightNode());
}
}
二叉查找树
二叉查找树 (binary search tree),简称为 BST,其特点为
- 它是一个二叉树
- 当前根节点的左子节点,要比根节点小
- 当前根节点的右子节点,要比根节点大
二叉树的提出其实主要就是为了提高查找效率,比如我们常用的
HashMap在处理哈希冲突严重时,拉链过长导致查找效率降低,就引入了红黑树。我们知道,二分查找可以缩短查找的时间,但是它要求查找的数据必须是有序的。每次查找、操作时都要维护一个有序的数据集,于是有了二叉查找树这个概念。可以看出,二叉查找树非常适合数字的查找和排序。
动态创建二叉树(二叉查找树)
在实际场景中,经常会遇到给定一个数组,将该数组转换为一个二叉树。为了后续数据排序和查找的方便,我们一般会创建一个二叉查找树。
代码实现思路也较为简单
- 如果比当前根节点要小,那么放到当前根节点左边
- 如果比当前根节点要大,那么放到当前根节点右边
因为是动态创建的,因此,需要用一个类来表示根节点。
public class TreeRoot {
private TreeNode treeRoot;
public TreeNode getTreeRoot() {
return treeRoot;
}
public void setTreeRoot(TreeNode treeRoot) {
this.treeRoot = treeRoot;
}
}
下面给出代码实现。
/** * 动态创建二叉查找树 * * @param treeRoot 根节点 * @param value 节点的值 */
public static void createTree(TreeRoot treeRoot, int value) {
//如果树根为空(第一次访问),将第一个值作为根节点
if (treeRoot.getTreeRoot() == null) {
TreeNode treeNode = new TreeNode(value);
treeRoot.setTreeRoot(treeNode);
} else {
//当前树根
TreeNode tempRoot = treeRoot.getTreeRoot();
while (tempRoot != null) {
//当前值大于根值,往右边走
if (value > tempRoot.getValue()) {
//右边没有树根,那就直接插入
if (tempRoot.getRightNode() == null) {
tempRoot.setRightNode(new TreeNode(value));
return ;
} else {
//如果右边有树根,到右边的树根去
tempRoot = tempRoot.getRightNode();
}
} else {
//左没有树根,那就直接插入
if (tempRoot.getLefTreeNode() == null) {
tempRoot.setLefTreeNode(new TreeNode(value));
return;
} else {
//如果左有树根,到左边的树根去
tempRoot = tempRoot.getLefTreeNode();
}
}
}
}
}
最后给出一个测试代码,进行验证
// 测试代码
int[] arrays = {2, 3, 1, 4, 5};
//动态创建树
TreeRoot root = new TreeRoot();
for (int value : arrays) {
createTree(root, value);
}
//先序遍历树
preTraverseBTree(root.getTreeRoot());
System.out.println("---------------先序遍历树");
//中序遍历树
inTraverseBTree(root.getTreeRoot());
System.out.println("---------------中序遍历树");
输出结果为
1
2
3
4
5
---------------先序遍历树
2
1
3
4
5
---------------中序遍历树
查询树的最大值
对于二叉查找树,中序遍历二叉查找树,得到的结果是就是按照数据大小排序的,因此可以直接获取树的最大值。
如果二叉树不是二叉查找树,要如何查询树的最大值呢? 可以采用递归思路实现
- 先查找左边子树的最大值
- 再查找右边子树的最大值
- 最后将上述两个最大值和根节点数值进行比较
其代码实现如下。
/** * 找出树的最大值 * * @param rootTreeNode */
public static int getMax(TreeNode rootTreeNode) {
if (rootTreeNode == null) {
return -1;
} else {
//找出左边的最大值
int left = getMax(rootTreeNode.getLefTreeNode());
//找出右边的最大值
int right = getMax(rootTreeNode.getRightNode());
//与当前根节点比较
int currentRootValue = rootTreeNode.getValue();
//假设左边的最大
int max = left;
if (right > max) {
max = right;
}
if (currentRootValue > max) {
max = currentRootValue;
}
return max ;
}
}
二叉查找树的性能
在最好的情况下,二叉排序树的查找效率比较高,是 O(logn),其访问性能近似于折半查找。但最差时候会是 O(n),比如插入的元素是有序的,生成的二叉排序树就是一个链表,这种情况下,需要遍历全部元素才行(见下图)。
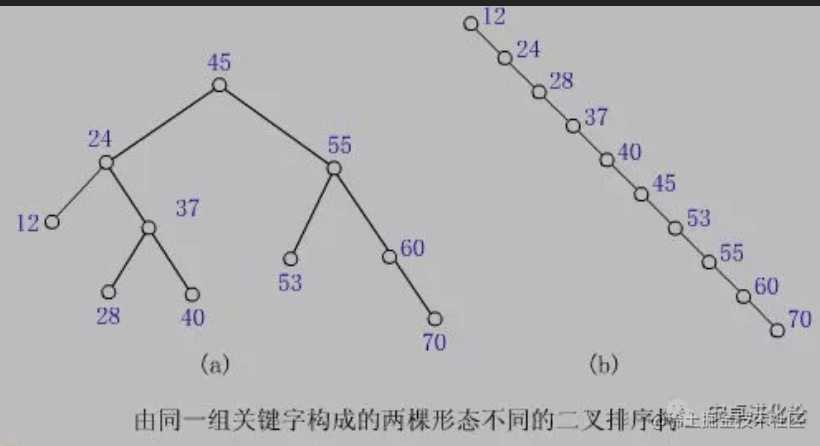
如果我们可以保证二叉排序树不出现上面提到的极端情况(插入的元素是有序的,导致变成一个链表),就可以保证很高的效率了。
但这在插入有序的元素时不太好控制,按二叉排序树的定义,我们无法判断当前的树是否需要调整。
因此就要用到平衡二叉树(AVL 树)了。
平衡二叉树
平衡二叉树 (AVL 树) 的提出,就是为了保证树不至于太倾斜,尽量保证两边平衡。因此它的定义如下
- 平衡二叉树要么是一棵空树
- 要么保证左右子树的高度之差不大于 1
- 子树也必须是一颗平衡二叉树
也就是说,树的两个左子树的高度差别不会太大。
此处,接着看前面的极端情况的二叉排序树,现在用它来构造一棵平衡二叉树。
以 12 为根节点,当添加 24 为它的右子树后,根节点的左右子树高度差为 1,这时还算平衡,这时再添加一个元素 28
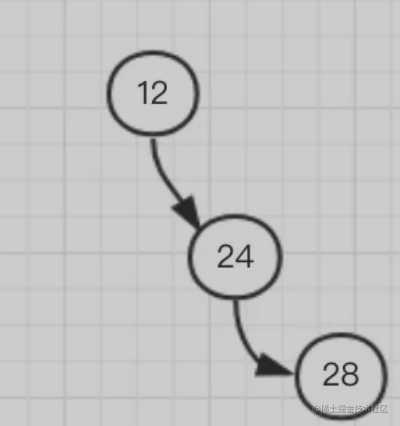
这时根节点 12 觉得不平衡了,我左孩子一个都没有,右边都有俩了,超过了之前说的最大为 1,不行,给我调整!
于是我们就需要调整当前的树结构,让它进行旋转。
因为最后一个节点加到了右子树的右子树,就要想办法给右子树的左子树加点料,因此需要逆时针旋转,将 24 变成根节点,12 右旋成 24 的左子树,就变成了这样
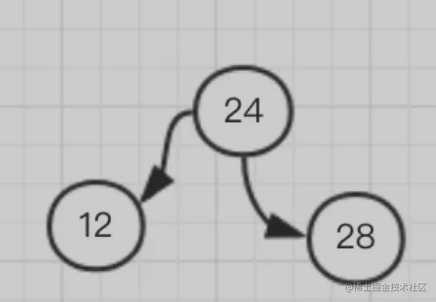
这时又恢复了平衡,再添加 37 到 28 的右子树,还算平衡
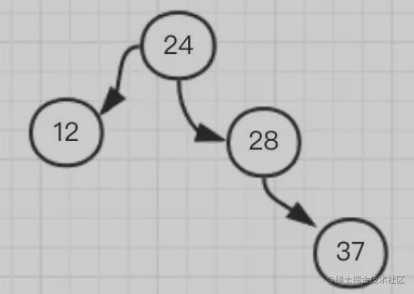
这时如果再添加一个 30,它就需要在 37 的左子树
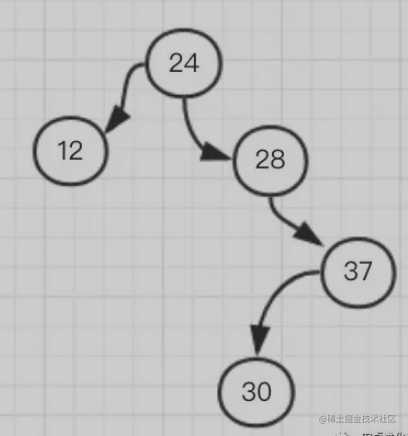
这时我们可以看到这个树又不平衡了,以 24 为根节点的树,明显右边太重,左边太稀,想要保持平衡就 24 得让位给 28,然后变成这样
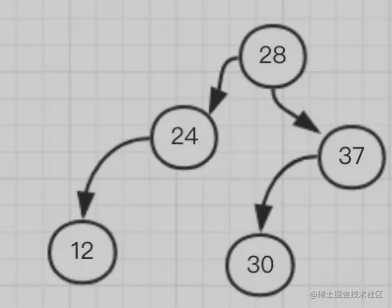
依次类推,平衡二叉树在添加和删除时需要进行旋转保持整个树的平衡,内部做了这么复杂的工作后,我们在使用它时,插入、查找的时间复杂度都是 O(logn),性能已经相当好了。
红黑树
Overview
红黑树(
Red–black tree)是一种自平衡二叉查找树,是在计算机科学中用到的一种数据结构,典型的用途是实现 关联数组。
红黑树本质上是一种二叉查找树,但它在二叉查找树的基础上额外添加了一个标记(颜色),同时具有一定的规则。这些规则使红黑树保证了一种平衡,插入、删除、查找的最坏时间复杂度都为 O(logn)。
它的统计性能要好于平衡二叉树(AVL树),因此,红黑树在很多地方都有应用。比如在 Java 集合框架中,很多部分(HashMap, TreeMap, TreeSet 等) 都有红黑树的应用,这些集合均提供了很好的性能。
由于 TreeMap 就是由红黑树实现的,因此本文将使用 TreeMap 的相关操作的代码进行分析、论证。
红黑树特点
首先,补充一个术语 黑色高度 —— 从根节点到叶节点的路径上黑色节点的个数,叫做树的黑色高度。
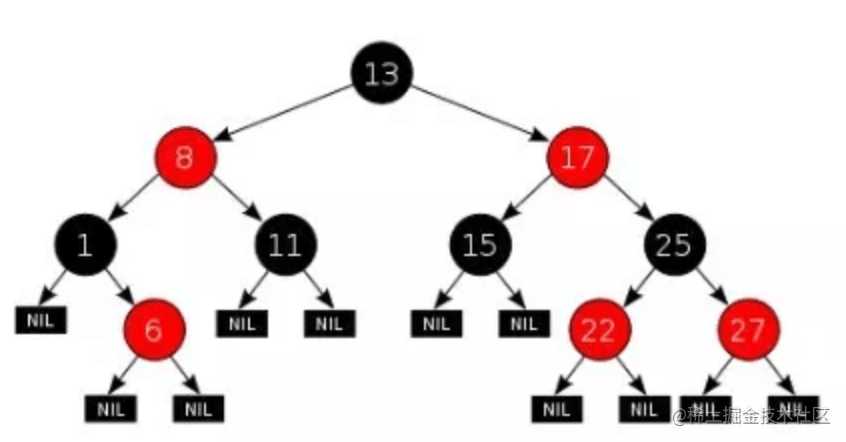
- Every node is either red or black. 每个节点要么是红色,要么是黑色。
- The root is black. 根节点永远是黑色的。
- Every leaf (NIL) is black. 所有的叶节点都是是黑色的(注意这里说叶子节点其实是上图中的 NIL 节点)。
- If a node is red, then both its children are black. 每个红色节点的两个子节点一定都是黑色。
- For each node, all simple paths from the node to descendant leaves contain the same number of black nodes. 从任一节点到其子树中每个叶子节点的路径都包含相同数量的黑色节点。
需要注意的是
- 性质 3 中指定红黑树的每个叶子节点都是空节点,而且并叶子节点都是黑色。但 Java 实现的红黑树将使用
null来代表空节点,因此遍历红黑树时将看不到黑色的叶子节点,反而看到每个叶子节点都是红色的。 - 性质 4 的意思是,从每个根到节点的路径上不会有两个连续的红色节点,但黑色节点是可以连续的。因此若给定黑色节点的个数 N,最短路径的情况是连续的 N 个黑色,树的高度为
N - 1;最长路径的情况为节点红黑相间,树的高度为2(N - 1) - 性质 5 是成为红黑树最主要的条件,后序的插入、删除操作都是为了遵守这个规定。
- 红黑树并不是标准平衡二叉树,它以性质 5 作为一种平衡方法,使自己的性能得到了提升。
红黑树的左旋右旋

红黑树的左右旋是比较重要的操作,左右旋的目的是调整红黑节点结构,转移黑色节点位置,使其在进行插入、删除后仍能保持红黑树的 5 条性质。
比如 X 左旋(右图转成左图)的结果,是让在 Y 左子树的黑色节点跑到 X 右子树去。
我们以 Java 集合框架中的 TreeMap 中的代码来看下左右旋的具体操作方法
- 指定节点 x 的左旋 (右图转成左图)
//这里 p 代表 x
private void rotateLeft(Entry p) {
if (p != null) {
Entry r = p.right; // p 是上图中的 x,r 就是 y
p.right = r.left; // 左旋后,x 的右子树变成了 y 的左子树 β
if (r.left != null)
r.left.parent = p; //β 确认父亲为 x
r.parent = p.parent; //y 取代 x 的第一步:认 x 的父亲为爹
if (p.parent == null) //要是 x 没有父亲,那 y 就是最老的根节点
root = r;
else if (p.parent.left == p) //如果 x 有父亲并且是它父亲的左孩子,x 的父亲现在认 y 为左孩子,不要 x 了
p.parent.left = r;
else //如果 x 是父亲的右孩子,父亲就认 y 为右孩子,抛弃 x
p.parent.right = r;
r.left = p; //y 逆袭成功,以前的爸爸 x 现在成了它的左孩子
p.parent = r;
}
}
可以看到,x 节点的左旋就是把 x 变成 右孩子 y 的左孩子,同时把 y 的左孩子送给 x 当右子树。
简单点记就是:左旋把右子树里的一个节点(上图 β)移动到了左子树。
- 指定节点 y 的右旋(左图转成右图)
private void rotateRight(Entry p) {
if (p != null) {
Entry l = p.left;
p.left = l.right;
if (l.right != null) l.right.parent = p;
l.parent = p.parent;
if (p.parent == null)
root = l;
else if (p.parent.right == p)
p.parent.right = l;
else p.parent.left = l;
l.right = p;
p.parent = l;
}
}
同理,y 节点的右旋就是把 y 变成 左孩子 x 的右孩子,同时把 x 的右孩子送给 x 当左子树。
简单点记就是:右旋把左子树里的一个节点(上图 β)移动到了右子树。
了解左旋、右旋的方法及意义后,就可以了解红黑树的主要操作:插入、删除。
红黑树的平衡插入
参考 面试旧敌之红黑树 | 掘金。
红黑树的平衡删除
参考 面试旧敌之红黑树 | 掘金。
B树
Overview
B树,也称 B- 树,它是一颗多路平衡查找树。我们描述一颗 B 树时需要指定它的阶数,阶数表示了一个结点最多有多少个孩子结点,一般用字母 m 表示阶数。当 m 取 2 时,就是我们常见的二叉搜索树。
一颗 m 阶的 B 树定义如下
- 每个结点最多有
m-1个关键字 - 根结点最少可以只有1个关键字
- 非根结点至少有
Math.ceil(m/2)-1个关键字 - 每个结点中的关键字都按照从小到大的顺序排列,每个关键字的左子树中的所有关键字都小于它,而右子树中的所有关键字都大于它
- 所有叶子结点都位于同一层,或者说根结点到每个叶子结点的长度都相同
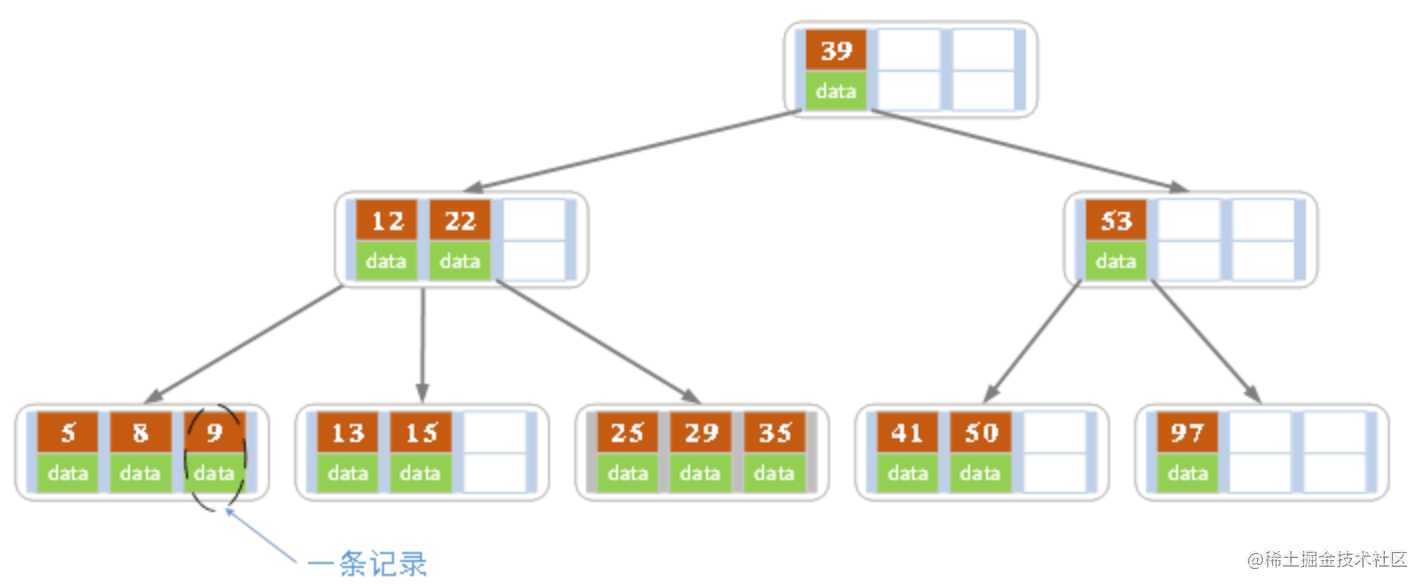
上图是一颗阶数为 4 的 B 树。在实际应用中的 B 树的阶数 m 都非常大(通常大于100),所以即使存储大量的数据,B 树的高度仍然比较小。
每个结点中存储了关键字(key)和关键字对应的数据(data),以及孩子结点的指针。我们将一个 key 和其对应的 data 称为一个记录。但为了方便描述,除非特别说明,后续文中就用 key 来代替 (key,llenvalue) 键值对这个整体。
在数据库中我们将 B 树(和 B+ 树)作为索引结构,可以加快查询速速,此时 B 树中的 key 就表示键,而 data 表示了这个键对应的条目在硬盘上的逻辑地址。
B树的插入操作
插入操作是指插入一条记录,即 (key,llenvalue) 的键值对。如果 B 树中已存在需要插入的键值对,则用需要插入的value 替换旧的 value。若 B 树不存在这个 key,则一定是在叶子结点中进行插入操作。
- 若该结点中关键码个数小于
m-1,则直接插入(对应的子节点) - 如该结点中关键码个数等于
m-1,则将引起结点的分裂。以中间关键码为界将结点一分为二,产生一个新结点,并把中间关键码插入到父结点(h-1层)中 - 向父亲结点插入中间关键字的时候,重复以上两个步骤。最坏情况是一直分裂到根结点,建立一个新的根结点,整个B树增加一层,如下图所示。
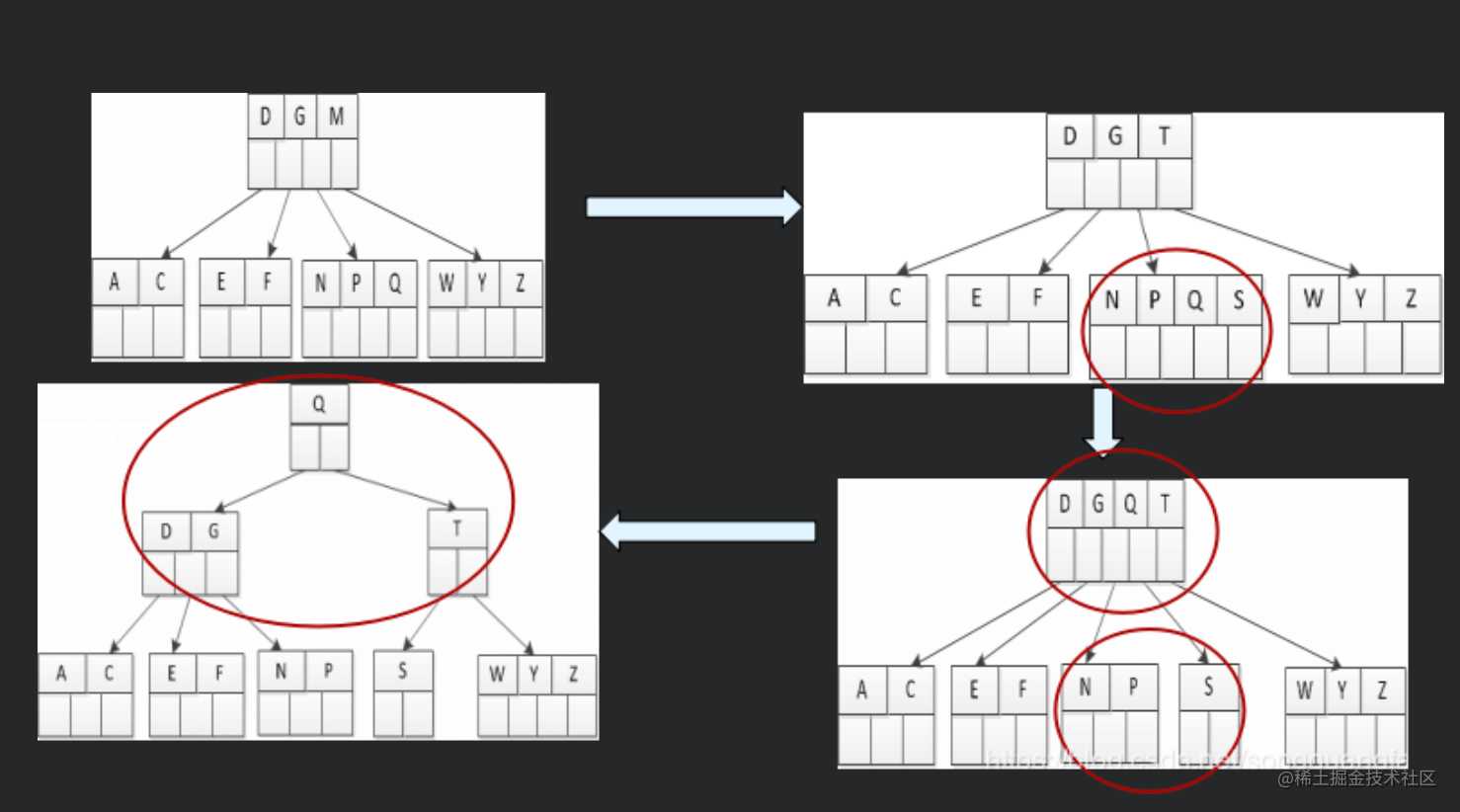
如上图所示,当试着向左上图中一个 4 阶的 B 树插入 S 时,插入后结点 NPQS 的关键字个数大于 4-1,所以进行分裂,分裂为 NP 和 S,并将中间关键字 Q 加入父亲结点,在这是发现父亲结点的关键字个数也超了,再次分裂,使得 Q 结点成为新的根结点,使得树的高度+1。
下面以 5 阶 B 树为例,介绍 B 树的插入操作,在 5 阶 B 树中,结点最多有 4 个 key,最少有 2 个 key。
- 在空树中插入 39

此时根结点就一个key,此时根结点也是叶子结点
- 继续插入22,97和41
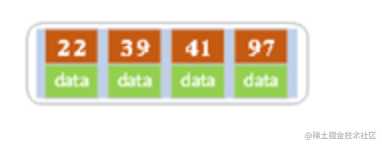
根结点此时有4个key
- 继续插入53

插入后超过了最大允许的关键字个数 4,所以以 key 值为 41 为中心进行分裂,结果如下图所示,分裂后当前结点指针指向父结点,满足 B 树条件,插入操作结束。当阶数 m 为偶数时,需要分裂时就不存在排序恰好在中间的 key,那么我们选择中间位置的前一个 key 或中间位置的后一个 key 为中心进行分裂即可。
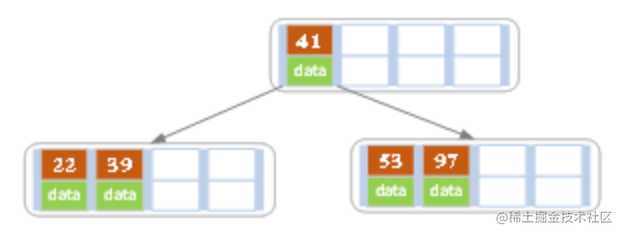
- 依次插入13,21,40,同样会造成分裂,结果如下图所示
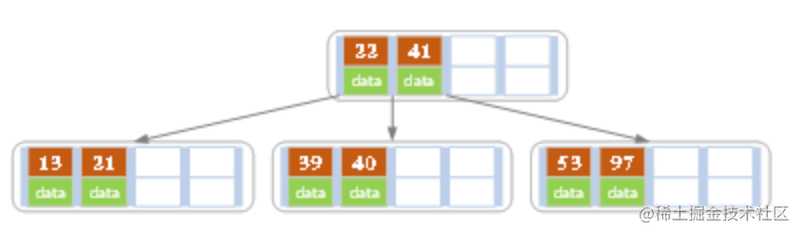
- 依次插入30,27, 33 ;36,35,34 ;24,29,结果如下图所示
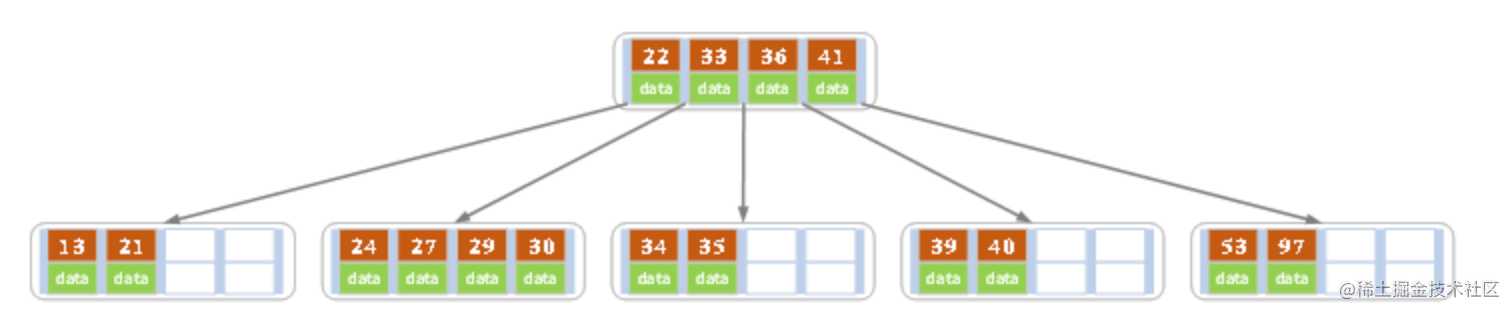
(1)插入 30,27,33后,对应节点表现如下,此时超出了最大允许的关键字个数4,将中间关键字 33 分裂,提升到父节点
|27|30|33|39|40|
(2)插入 36,35,34 后,对应节点表现如下,此时超出了最大允许的关键字个数4,将中间关键字 36 分裂,提升到父节点
|34|35|36|39|40|
- 插入key值为26的记录,插入后的结果如下图所示
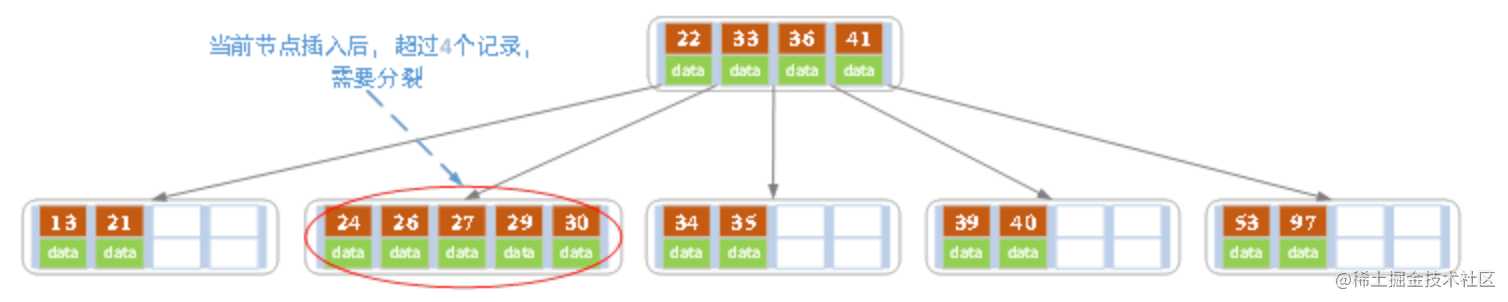
当前结点需要以27为中心分裂,并向父结点进位27,然后当前结点指向父结点,结果如下图所示。

进位后导致当前结点(即根结点)也需要分裂,分裂的结果如下图所示。
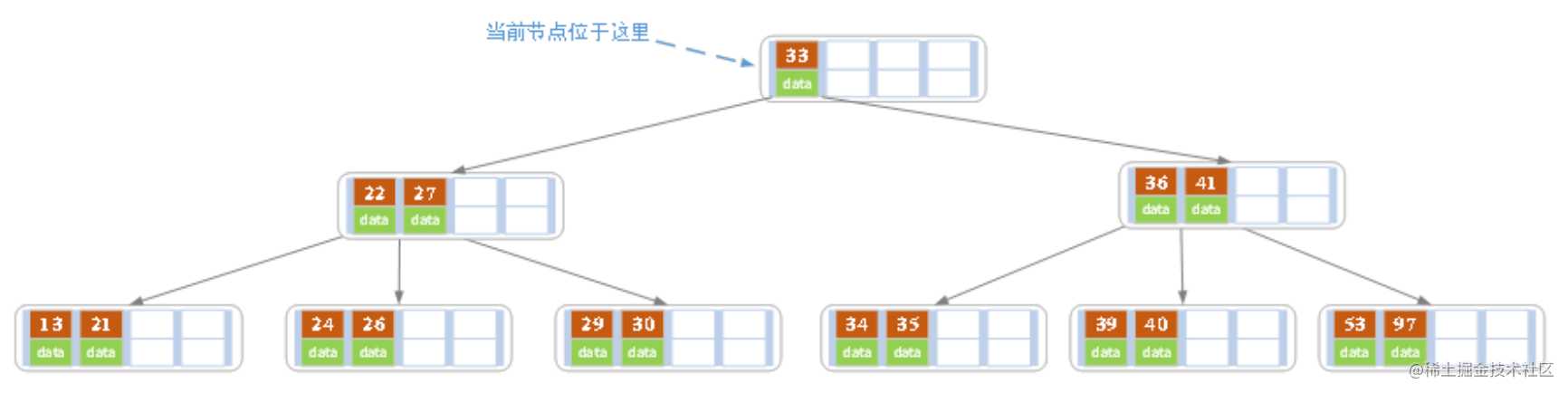
分裂后当前结点指向新的根,此时无需调整。
- 最后再依次插入key为17,28,29,31,32的记录,结果如下图所示
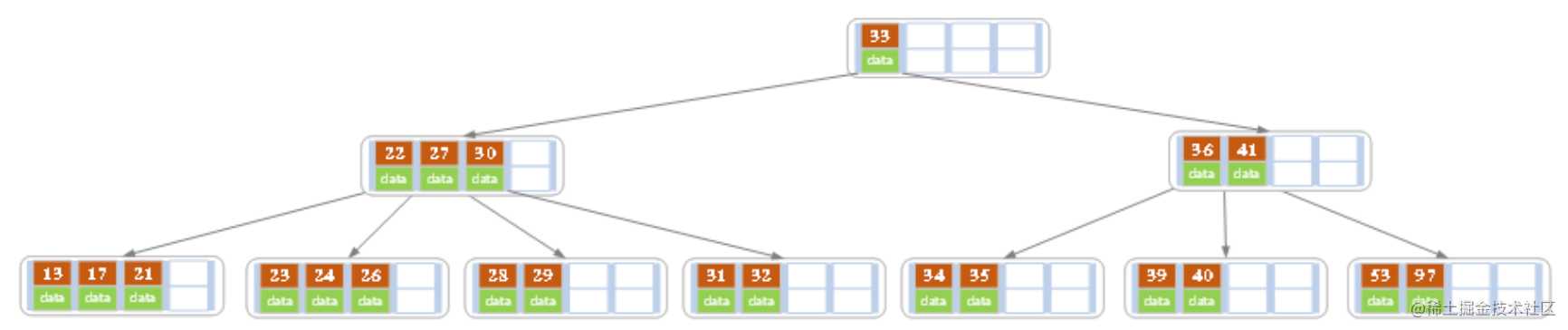
在实现 B 树的代码中,为了使代码编写更加容易,我们可以将结点中存储记录的数组长度定义为 m 而非 m-1,这样方便底层的结点由于分裂向上层插入一个记录时,上层有多余的位置存储这个记录。同时,每个结点还可以存储它的父结点的引用,这样就不必编写递归程序。
一般来说,对于确定的 m 和确定类型的记录,结点大小是固定的,无论它实际存储了多少个记录。但是分配固定结点大小的方法会存在浪费的情况,比如key 为 28,29 所在的结点,还有 2 个 key 的位置没有使用,但是已经不可能继续在插入任何值了,因为这个结点的前序 key 是 27,后继key 是30,所有整数值都用完了。所以如果记录先按 key 的大小排好序,再插入到B树中,结点的使用率就会很低,最差情况下使用率仅为 50%。
B树的删除
删除操作是指,根据 key 删除记录,如果 B 树中的记录中不存对应 key 的记录,则删除失败。
- 如果当前需要删除的 key 位于非叶子结点上,则用后继 key(这里的后继 key 均指后继记录的意思)覆盖要删除的 key,然后在后继 key 所在的子支中删除该后继 key。此时后继 key 一定位于叶子结点上,这个过程和二叉搜索树删除结点的方式类似。删除这个记录后执行第2步
- 该结点 key 个数大于等于
Math.ceil(m/2)-1,结束删除操作,否则执行第3步。 - 如果兄弟结点 key 个数大于
Math.ceil(m/2)-1,则父结点中的 key 下移到该结点,兄弟结点中的一个 key 上移,删除操作结束。 - 否则,将父结点中的 key 下移与当前结点及它的兄弟结点中的 key 合并,形成一个新的结点。原父结点中的 key 的两个孩子指针就变成了一个孩子指针,指向这个新结点。然后当前结点的指针指向父结点,重复上第2步。
有些结点它可能即有左兄弟,又有右兄弟,那么我们任意选择一个兄弟结点进行操作即可。
下面以 5 阶 B 树为例,介绍 B 树的删除操作,5阶B树中,结点最多有 4 个key,最少有 2 个key。
- 原始状态
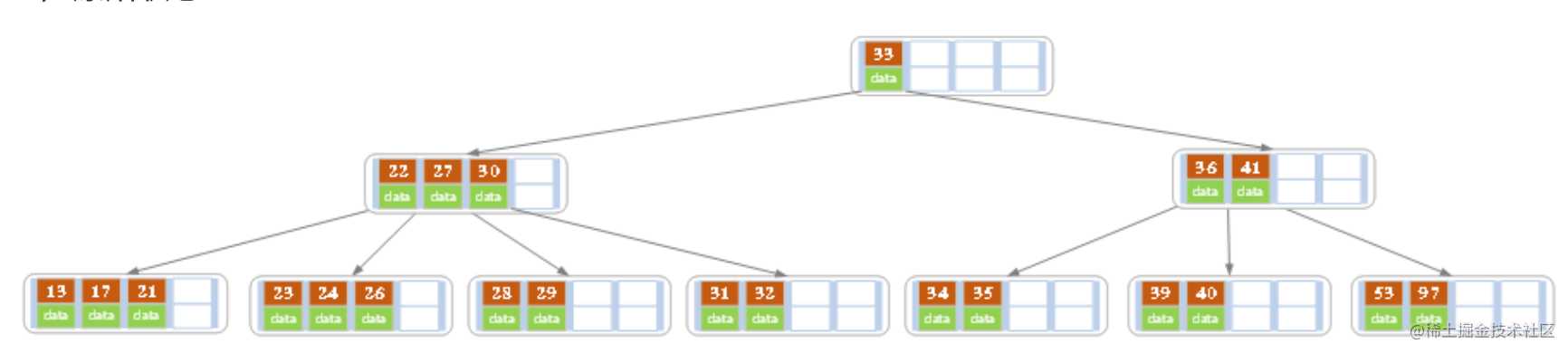
- 在上面的B树中删除21,删除后结点中的关键字个数仍然大于等2,所以删除结束
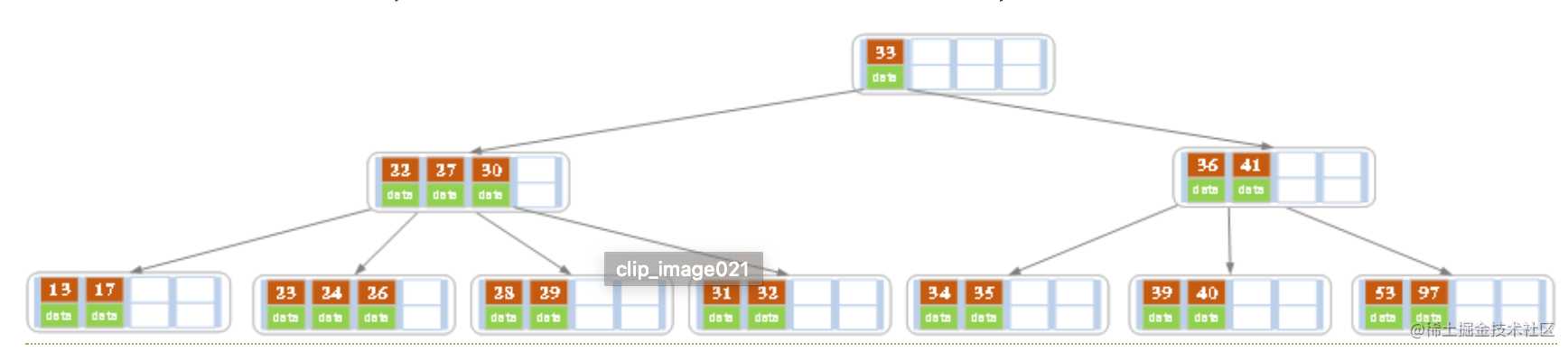
- 在上述情况下接着删除27。从上图可知 27 位于非叶子结点中,所以用 27 的后继替换它。从图中可以看出,27 的后继为 28,我们用28替换27,然后在28(原27)的右孩子结点中删除28。删除后的结果如下图所示
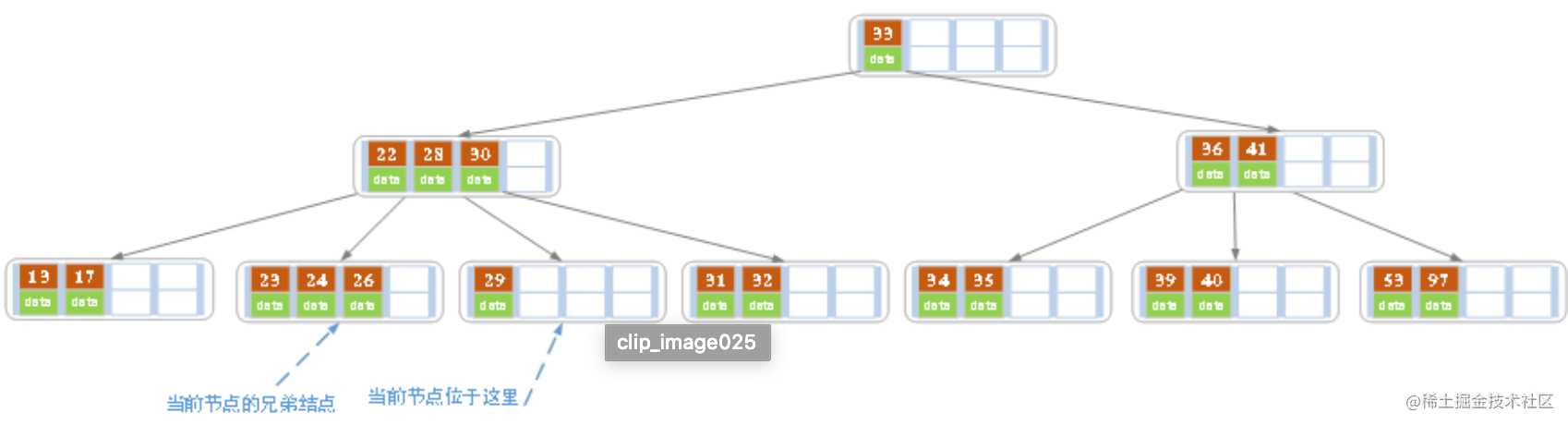
删除后发现,当前叶子结点的记录的个数小于2,而它的兄弟结点中有3个记录(当前结点还有一个右兄弟,选择右兄弟就会出现合并结点的情况,不论选哪一个都行,只是最后B树的形态会不一样而已),我们可以从兄弟结点中借取一个key。所以父结点中的28下移,兄弟结点中的26上移,删除结束。结果如下图所示。
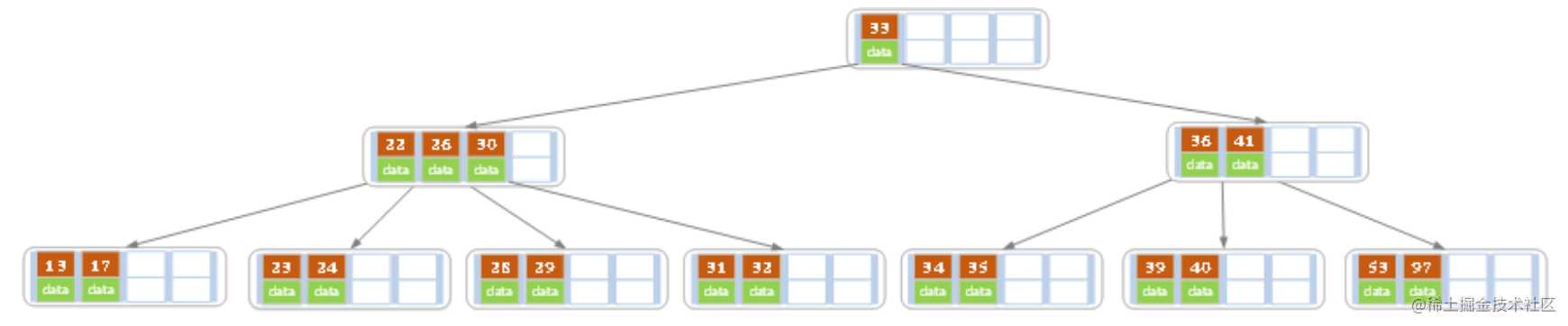
- 在上述情况下接着删除32,结果如下图
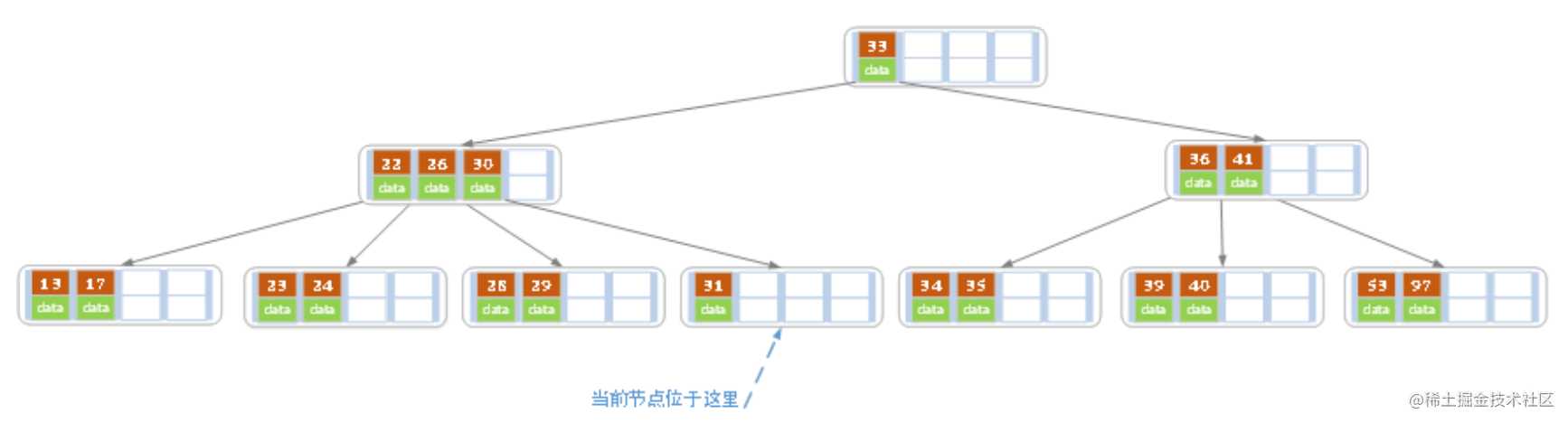
当删除后,当前结点中只有1个key,而兄弟结点中也仅有2个key。所以只能让父结点中的30下移和这个两个孩子结点中的key合并,成为一个新的结点,当前结点的指针指向父结点。结果如下图所示。
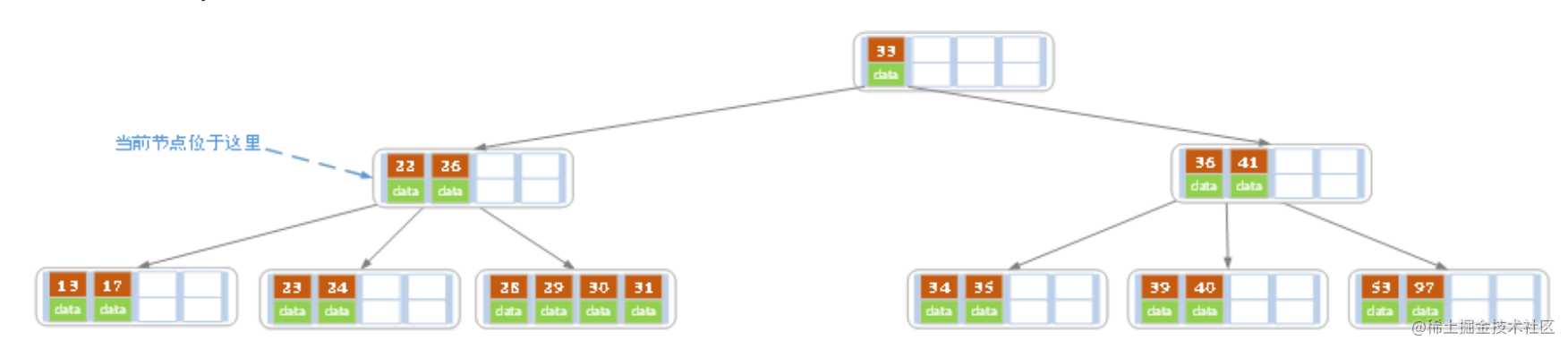
当前结点key的个数满足条件,故删除结束。
- 上述情况下,我们接着删除key为40的记录,删除后结果如下图所示
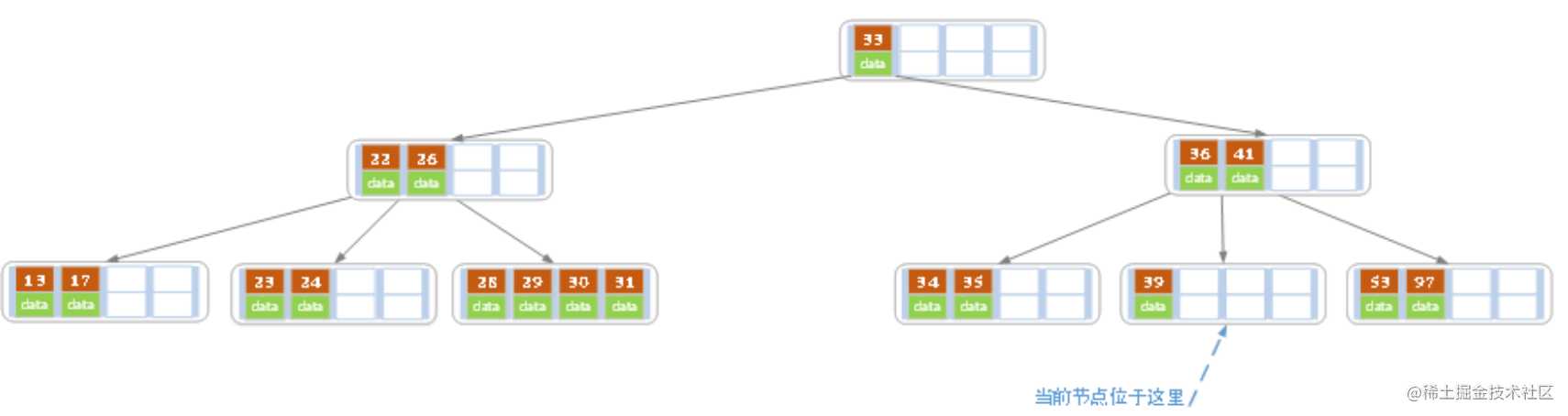
同理,当前结点的记录数小于2,兄弟结点中没有多余key,所以父结点中的key下移,和兄弟(这里我们选择左兄弟,选择右兄弟也可以)结点合并,合并后的指向当前结点的指针就指向了父结点。
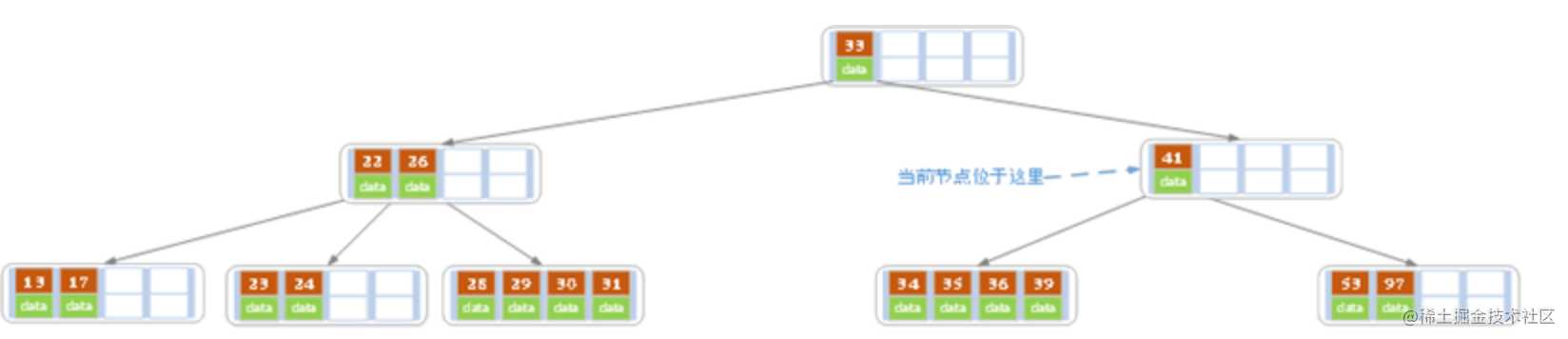
同理,对于当前结点而言只能继续合并了,最后结果如下所示。

合并后结点当前结点满足条件,删除结束。
B+树
Overview
B+树是一种树数据结构,通常用于数据库和操作系统的文件系统中。B+树的特点是能够保持数据稳定有序,其插入和修改拥有较稳定的对数时间复杂度。B+ 树元素自底向上插入,这与二叉树恰好相反。
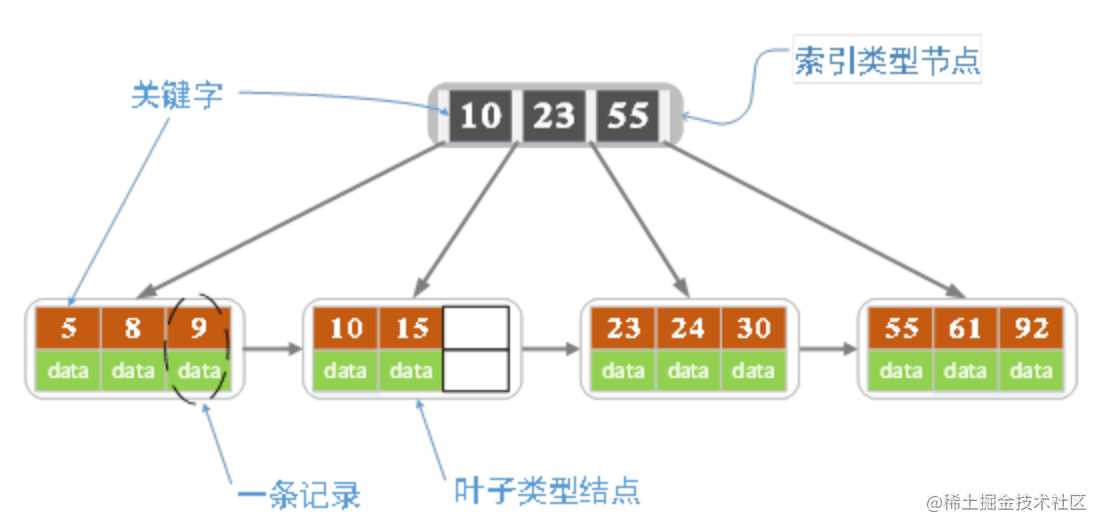
B+ 树是为磁盘或其他直接存取辅助设备而设计的一种平衡查找树,在 B+ 树中,所有记录节点都是按键值的大小顺序存放在同一层的叶节点中,各叶节点指针进行连接。
各种资料上 B+ 树的定义各有不同,一种定义方式是关键字个数和孩子结点个数相同。这里我们采取 维基百科 上所定义的方式,即关键字个数比孩子结点个数小1,这种方式是和B树基本等价的。上图就是一颗阶数为4的B+树。
除此之外B+树还有以下的要求
- B+ 树包含 2 种类型的结点:内部结点(也称索引结点)和叶子结点。根结点本身即可以是内部结点,也可以是叶子结点。根结点的关键字个数最少可以只有1个。
- B+树与B树最大的不同是内部结点不保存数据,只用于索引,所有数据(或者说记录)都保存在叶子结点中。
- m 阶 B+ 树表示了内部结点最多有
m-1个关键字(或者说内部结点最多有m个子树),阶数 m 同时限制了叶子结点最多存储 m-1 个记录。 - 内部结点中的 key 都按照从小到大的顺序排列,对于内部结点中的一个key,左树中的所有key都小于它,右子树中的key都大于等于它。叶子结点中的记录也按照key的大小排列。
- 每个叶子结点都存有相邻叶子结点的指针,叶子结点本身依关键字的大小自小而大顺序链接。
B+树的插入
- 若为空树,创建一个叶子结点,然后将记录插入其中,此时这个叶子结点也是根结点,插入操作结束。
- 针对叶子类型结点:根据 key 值找到叶子结点,向这个叶子结点插入记录。插入后,若当前结点 key 的个数小于等于 m-1,则插入结束。否则将这个叶子结点分裂成左右两个叶子结点,左叶子结点包含前
m/2个记录,右结点包含剩下的记录,将第m/2+1个记录的 key 进位到父结点中(父结点一定是索引类型结点),进位到父结点的 key 左孩子指针向左结点,右孩子指针向右结点。将当前结点的指针指向父结点,然后执行第3步。 - 针对索引类型结点:若当前结点 key 的个数小于等于
m-1,则插入结束。否则,将这个索引类型结点分裂成两个索引结点,左索引结点包含前(m-1)/2个key,右结点包含m-(m-1)/2个key,将第m/2个key进位到父结点中,进位到父结点的 key 左孩子指向左结点,进位到父结点的 key右孩子指向右结点。将当前结点的指针指向父结点,然后重复第3步。
下面是一颗5阶B树的插入过程,5阶B数的结点最少2个key,最多4个key。
- 空树中插入5
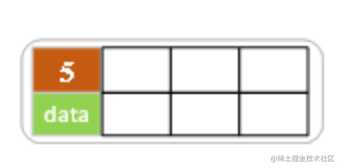
- 依次插入8,10,15

- 插入16

插入 16 后超过了关键字的个数限制,所以要进行分裂。在叶子结点分裂时,分裂出来的左结点 2 个记录,右边 3 个记录,中间 key 成为索引结点中的key,分裂后当前结点指向了父结点(根结点)。结果如下图所示。
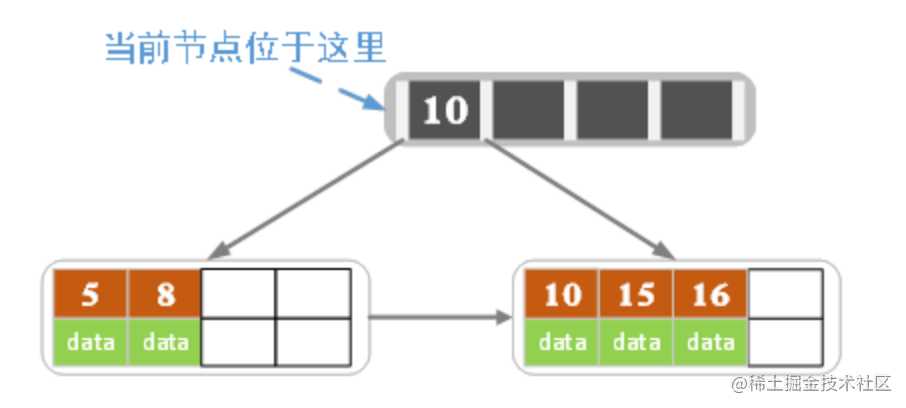
需要注意的是,分裂出来的父节点(图上灰色所示)是索引节点,不负责保存数据,因此数据10,依旧需要在右子节点中存储。
当然我们还有另一种分裂方式,给左结点3个记录,右结点2个记录,此时索引结点中的key就变为15。
- 插入17
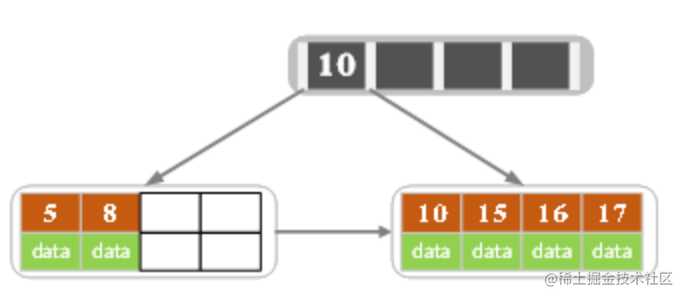
- 插入18,插入后如下图所示
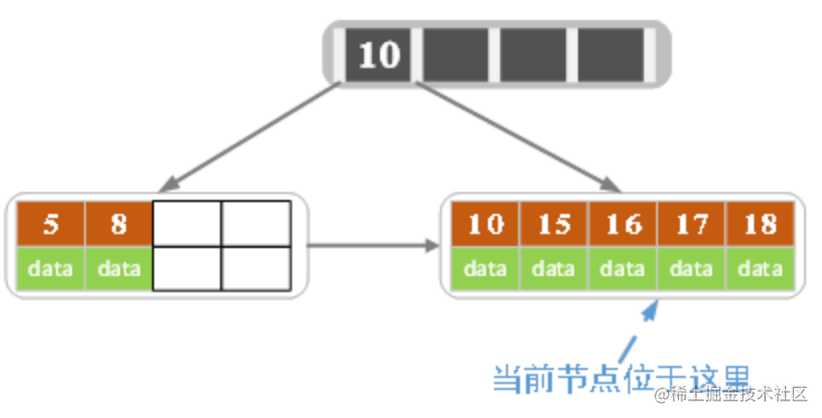
当前结点的关键字个数大于5,进行分裂。分裂成两个结点,左结点2个记录,右结点3个记录,关键字16进位到父结点(索引类型)中,将当前结点的指针指向父结点。
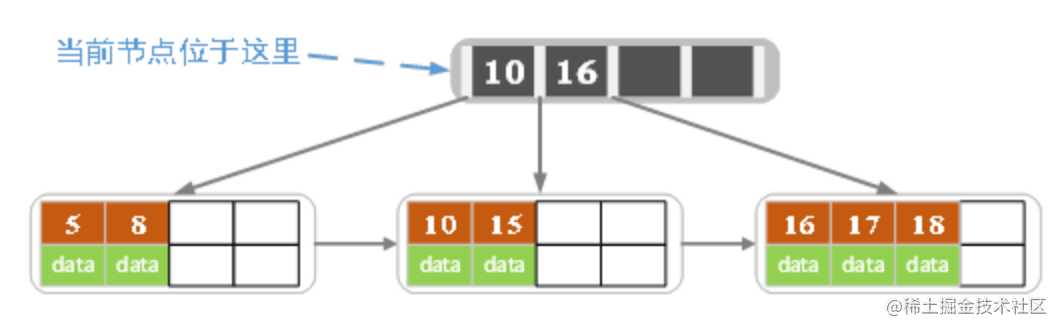
当前结点的关键字个数满足条件,插入结束。
- 插入若干数据后

- 在上图中插入7,结果如下图所示

当前结点的关键字个数超过4,需要分裂。左结点2个记录,右结点3个记录。分裂后关键字7进入到父结点中,将当前结点的指针指向父结点,结果如下图所示。

当前结点的关键字个数超过4,需要继续分裂。左结点2个关键字,右结点2个关键字,关键字16进入到父结点中,将当前结点指向父结点,结果如下图所示。
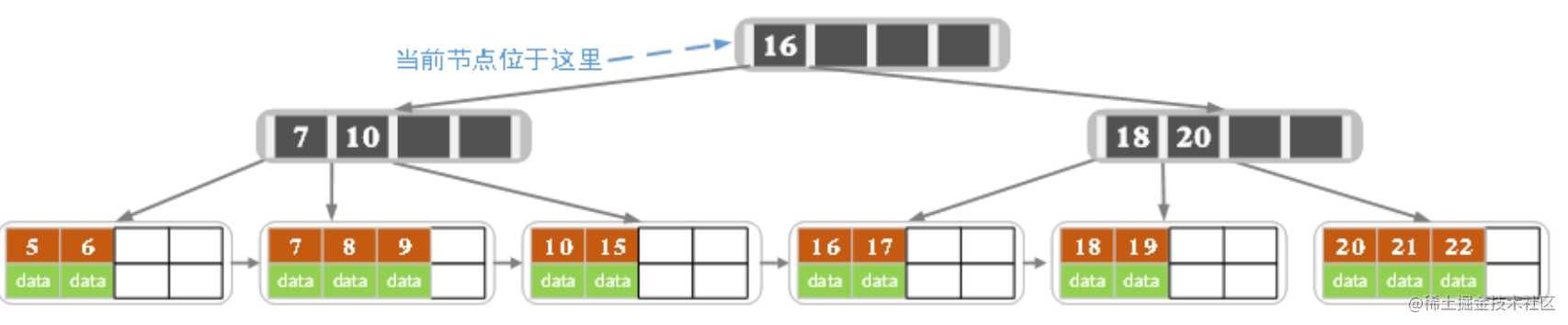
当前结点的关键字个数满足条件,插入结束。
B+树的删除
如果叶子结点中没有相应的key,则删除失败。否则执行下面的步骤
- 删除叶子结点中对应的key。删除后若结点的 key 的个数大于等于
Math.ceil(m-1)/2 – 1,删除操作结束,否则执行第2步。 - 若兄弟结点 key 有富余(大于
Math.ceil(m-1)/2 – 1),向兄弟结点借一个记录,同时用借到 的key 替换父结点(指当前结点和兄弟结点共同的父结点)中的key,删除结束。否则执行第3步。 - 若兄弟结点中没有富余的key,则当前结点和兄弟结点合并成一个新的叶子结点,并删除父结点中的key(父结点中的这个key两边的孩子指针就变成了一个指针,正好指向这个新的叶子结点),将当前结点指向父结点(必为索引结点),执行第4步(第4步以后的操作和B树就完全一样了,主要是为了更新索引结点)。
- 若索引结点的 key 的个数大于等于
Math.ceil(m-1)/2 – 1,则删除操作结束。否则执行第5步 - 若兄弟结点有富余,父结点key下移,兄弟结点key上移,删除结束。否则执行第6步
- 当前结点和兄弟结点及父结点下移key合并成一个新的结点。将当前结点指向父结点,重复第4步。
注意,通过B+树的删除操作后,索引结点中存在的key,不一定在叶子结点中存在对应的记录。
下面是一颗5阶B树的删除过程,5阶B数的结点最少2个key,最多4个key。
- 初始状态
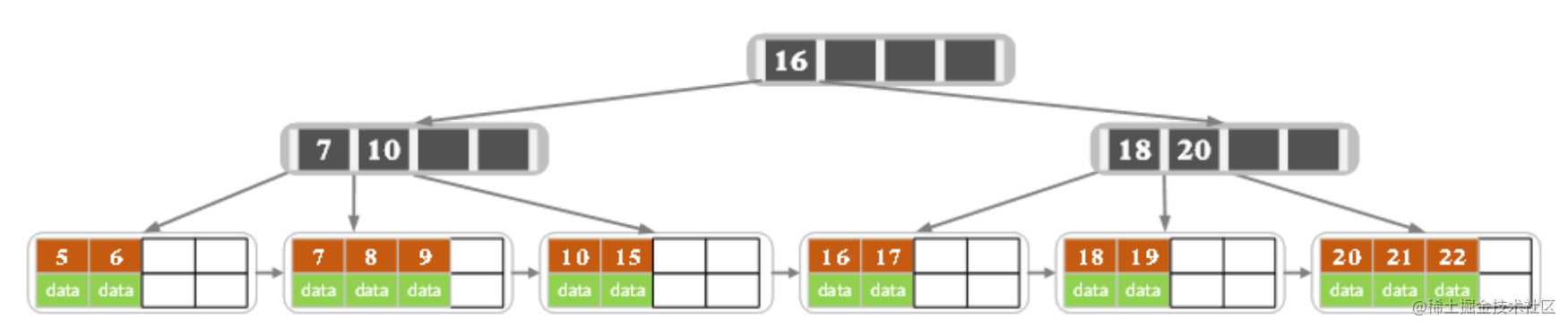
- 删除22,删除后结果如下图
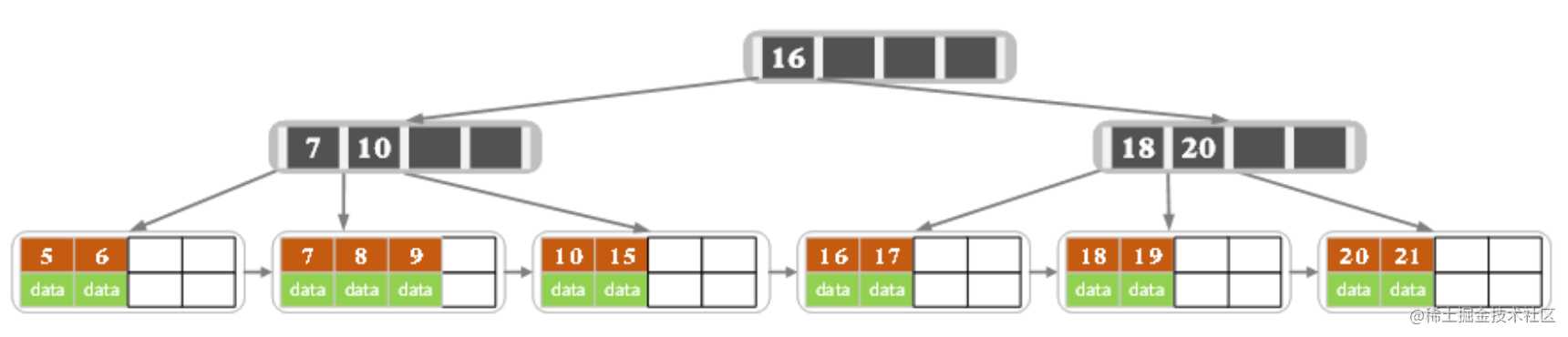
删除后叶子结点中key的个数大于等于2,删除结束
- 删除15,删除后的结果如下图所示
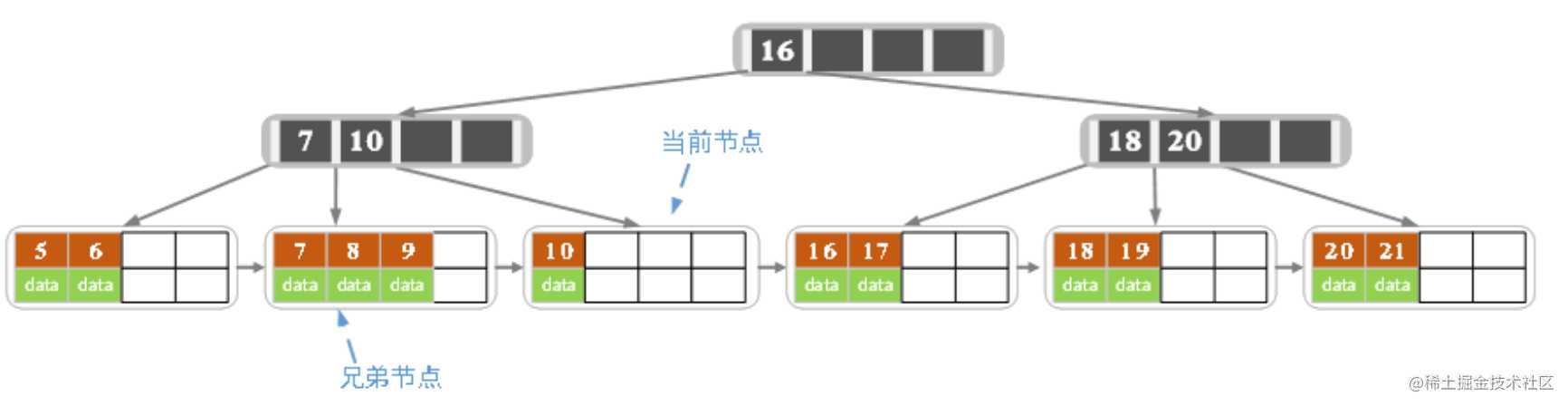
删除后当前结点只有一个key,不满足条件,而兄弟结点有三个key,可以从兄弟结点借一个关键字为9的记录,同时更新将父结点中的关键字由10也变为9,删除结束。
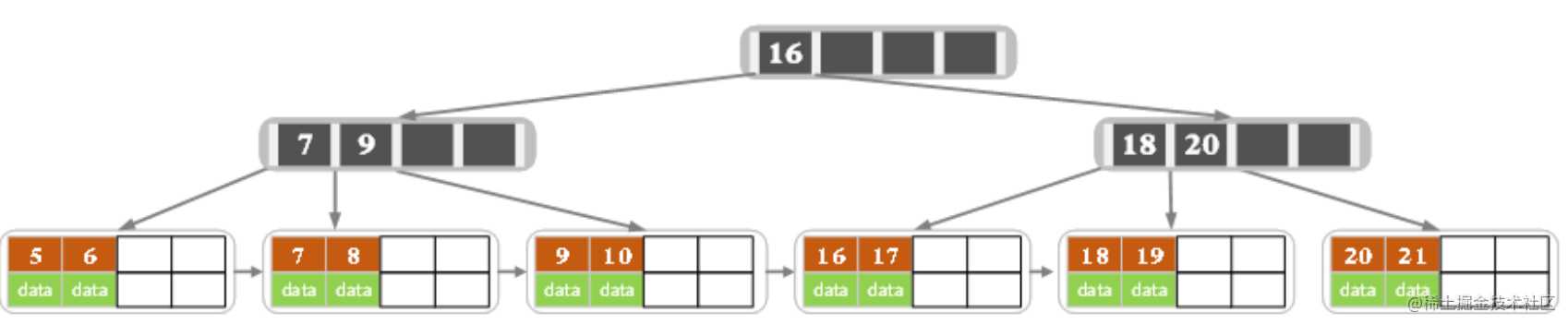
- 删除7,删除后的结果如下图所示
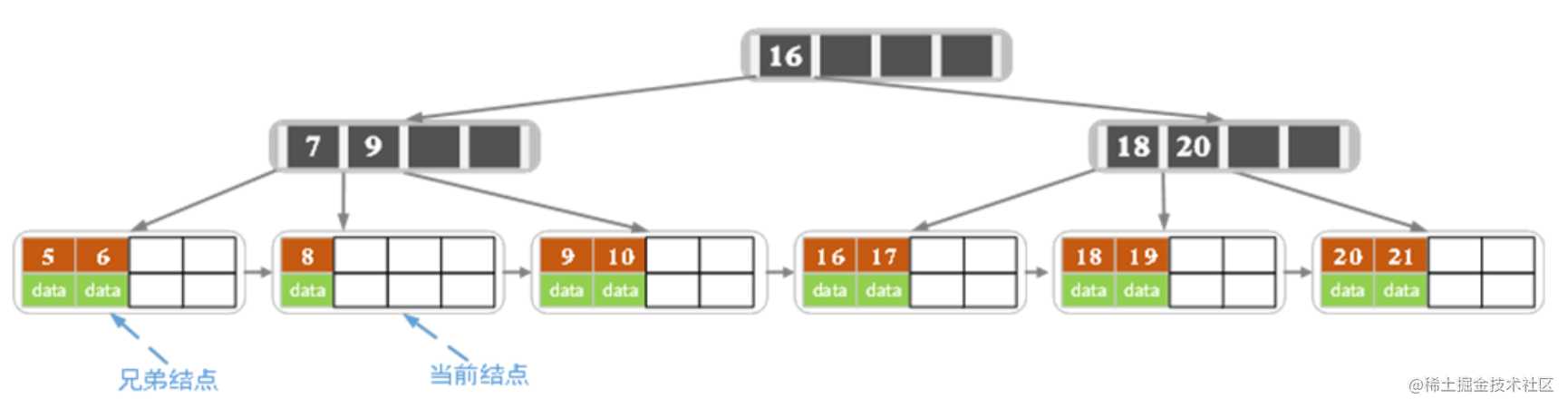
当前结点关键字个数小于2,(左)兄弟结点中的也没有富余的关键字(当前结点还有个右兄弟,不过选择任意一个进行分析就可以了,这里我们选择了左边的),所以当前结点和兄弟结点合并,并删除父结点中的key,当前结点指向父结点。
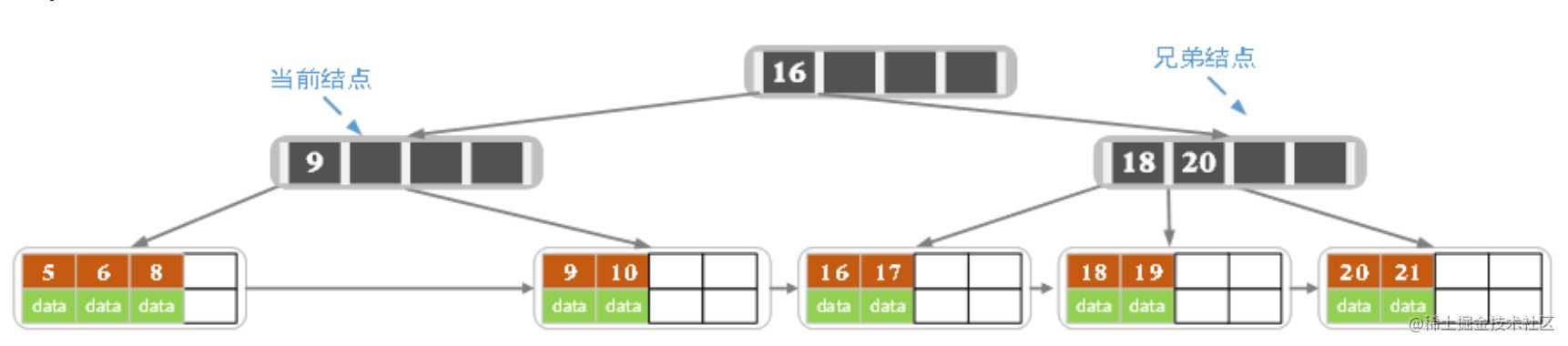
此时当前结点的关键字个数小于2,兄弟结点的关键字也没有富余,所以父结点中的关键字下移,和两个孩子结点合并,结果如下图所示。

MySQL 索引和B+树
今天的文章数据结构——二叉查找树,B+树,红黑树分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/17691.html
