【VRP】基于matlab遗传算法求解多VRP问题【含Matlab源码 010期】

一、简介

导语：车辆路径问题（vehicle routing problem，VRP）是比较经典的运筹学优化问题，在离散组合优化中研究较多，并在物流行业有着很强的应用价值，通过优化车辆行驶路径，能有效节省物流配送成本。车辆路线问题最早是由Dantzig和Ramser于1959年首次提出，由于配送路径优化问题是一个 NP-hard问题，因此，采用启发式算法求解该问题就成为人们研究的一个重要方向。经过全世界专家学者的不断研究，车辆路线问题研究取得了大量成果，在问题模型方面扩展了约束条件、优化目标等，更加符合现实生产生活场景，在求解方法方面主要通过启发式方法、精确方法、智能算法等，不断提高求解质量。本文本着学习交流的态度，从最基本的车辆路径问题入手，学习如何使用遗传算法求解车辆路径问题。
1、车辆路径问题概述
车辆路径问题(vehicle routing problem，VRP)给定一组有容量限制的车辆的集合、一个物流中心（或供货地）、若干有供货需求的客户，组织适当的行车路线，使车辆有序地通过所有的客户，在满足一定的约束条件（如需求量、服务时间限制、车辆容量限制、行驶里程限制等）下，达到一定的目标（如路程最短、费用极小、时间尽量少、使用车辆数尽量少等）。
本文以中国知网发表的高引用文章作参考，以配送总里程最短为目标函数，约束条件满足：(1)每条配送路径上各客户的需求量之和不超过配送车辆的载重量；(2)每条配送路径的长度不超过配送车辆一次配送的最大行驶距离；(3)每个客户的需求必须满足，且只能由一台配送车辆送货。（车辆路径优化问题的数学模型不再此处讨论）
2、遗传算法
遗传算法（Genetic Algorithm, GA）是一种较为经典的智能优化算法，经大量的研究表明，其在求解离散组合优化问题中有着优异的表现。遗传算法的思想为优胜劣汰，通过交叉操作、变异操作获得多样性的解，在下一代中保留目标函数最优的解，并通过轮盘赌方式选择下一代个体，不断循环迭代，从而不断优化问题的解。本文采用Matlab R2010b编程实现，遗传算法求解车辆路径问题的具体内容及步骤如下：
2.1. 编码操作
车辆路径问题为离散优化问题，结合约束条件3：每个客户的需求必须满足，且只能由一台配送车辆送货，可以以客户整数编号的排序进行编码，保证每个客户编号能且只能出现一次。比如说：客户数量为8，则编码的染色体可以为1-2-3-4-5-6-7-8。

二、运行结果

%population_num种群规模；Customer_num客户数量
population=zeros(population_num,Customer_num);
for i=1:population_num
     population(i,:)=randperm(Customer_num);
end
```2.2. 解码操作
解码操作需要在满足约束条件1、2的前提下，将染色体解码为车辆的配送路径，为计算目标值做好准备。根据排列顺序进行解码，主要判断该客户加入到车辆配送路径后，是否满足该车的最大行驶距离，是否满足该车的最大载重量。比如说染色体1-2-3-4-5-6-7-8，第1辆车路径：将客户1加入到该车的路径中，则第1辆车的行驶路线为0-1-0，表示，该车从物流中心0出发，将货物运到客户1，再返回物流中心，计算行驶距离是否满足第1辆车的最大行驶距离，同时计算运货量是否满足第1辆车的最大载货量，再确定客户2如果加入第1辆车的路径是否满足以上2个条件，如果满足，则第1辆车的行驶路线为0-1-2-0，依次类推，如果不满足其中的1个条件，则需要增加1辆车即为从物流中心出发的第2条行驶路线。
2.3. 计算目标值
根据解码出来的车辆行驶路径，计算目标值即为总配送里程。但需要判断解码出来的行驶路径的数量是否超过总车辆数，若未超过则按所有车辆路径相加得到总配送里程，若超过总车辆数，则说明该配送路径不可行，该解为不可行解，因该问题为最小化优化问题，可通过罚函数增大目标值来淘汰掉该不可行解。
2.4. 交叉操作
交叉操作是根据两个父代的染色体信息，根据交叉概率Pc交换某些片段，从而使父代的信息能够遗传给子代，本质是根据父代的染色体信息产生子代（新解），交叉操作的实现方式有多种，本文给出了一种交换染色体片段的交叉操作，如下图所示。
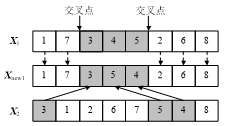
![在这里插入图片描述](https://p3-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/e5b1bb18a7574f14955e943463e59c4d~tplv-k3u1fbpfcp-zoom-1.image)
2.5. 变异操作
变异操作是在父代的染色体信息基础上，根据变异概率Pm改变某些基因位，从而使整个染色体发生变化，该操作对染色体的改变程度小于交叉操作，变异操作的实现方式有多种，本文给出了一种单点位基因突变的变异操作，如下图所示。
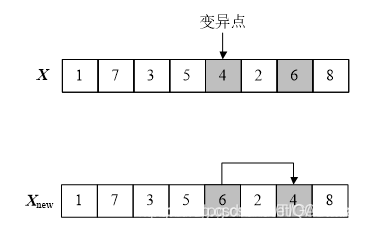
![在这里插入图片描述](https://p3-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/fe37518d0c664c628deb69f5f8a4082a~tplv-k3u1fbpfcp-zoom-1.image)
2.6. 选择操作
选择操作以目标值较好的染色体及随机产生的新染色体组成，在确保优良基因能传递给下一代的基础上，通过随机产生的新解扩大染色体的多样性。
2.7. 算法流程
遗传算法求解车辆路径问题的算法步骤如下：
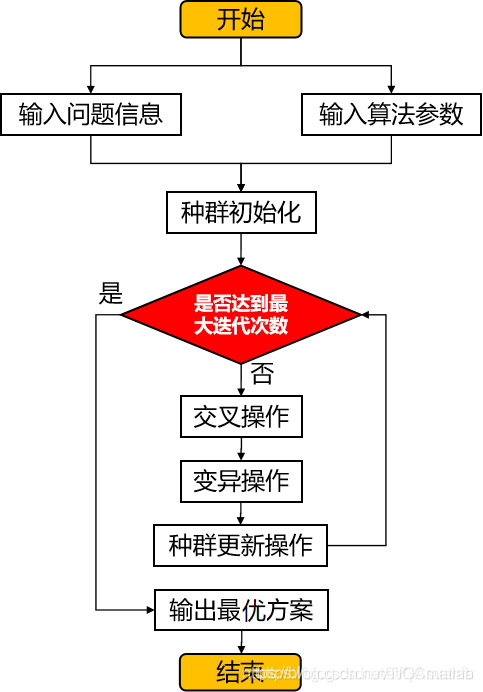
![在这里插入图片描述](https://p3-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/58f4289c65294c59baed14e265fc5d76~tplv-k3u1fbpfcp-zoom-1.image)
3、算法验证
实例1：某物流中心有2台配送车辆，其载重量均为8t，车辆每次配送的最大行驶距离为50Km，配送中心（编号为0）与8个客户之间及8个客户相互之间的距离dij、8个客户的货物需求量qj（i, j=1，2，……，8）见下表1。要求合理安排车辆配送路线，使配送总里程最短。
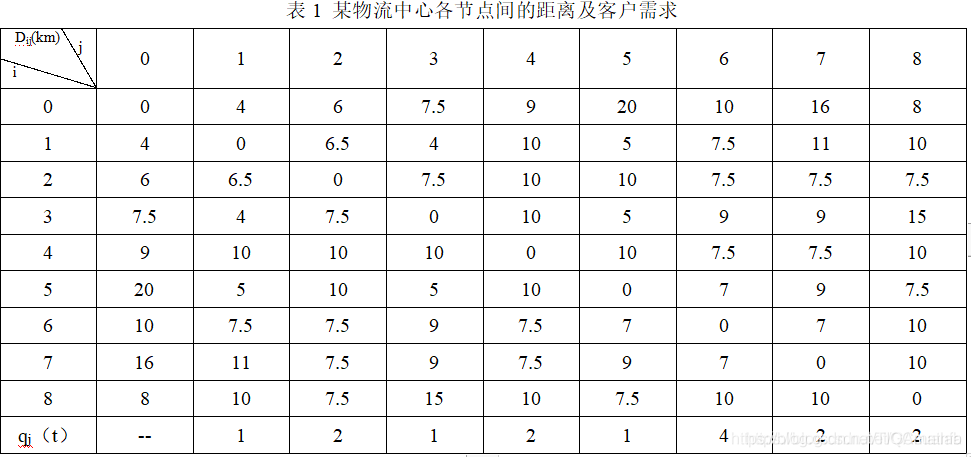
![在这里插入图片描述](https://p3-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/277aaf91293e4be699623d78ba84779a~tplv-k3u1fbpfcp-zoom-1.image)
根据以上问题的数据信息，设置好遗传算法的参数，通过遗传算法求解该车辆路径问题得到最有解为【1-3-5-6-4-7-2-8】，最短距离为【69.5】，解码操作得到的车辆路径为【0-1-3-5-6-0】、【0-4-7-2-8-0】。本文通过遗传算法求解实例1，得到与参考文献一致的最短距离，验证了算法的正确性。

```c
%% 遗传算法 优化函数
clc;close all;clear all;%清除变量
rand('seed', 100);
 
global XY p nodenumber maxlink;
filename='需求点分布.xlsx';
[adata,bdata,cdata]=xlsread(filename);
XY=adata(2:end,:)'; nodenumber=size(XY,1); p=4;% 配送中心个数 maxlink=5;% 最大连接数 N=p*2;%优化问题 lb=[min(XY(:,1))*ones(1,p),min(XY(:,2))*ones(1,p)]; ub=[max(XY(:,1))*ones(1,p),max(XY(:,2))*ones(1,p)]; % 遗传算法参数 popsize=200;%遗传算法种群数 ga_max=500;%遗传算法迭代次数 PM=0.05;%变异概率 PC=0.8;%交叉概率 %% 遗传算法主程序 %性能跟踪 tracemat=zeros(ga_max,2); gen=0; tic; Chrom=genChrome(popsize,N,lb,ub);% 建立种群 Value=decodingFun(Chrom,popsize);%解码染色体 %% 遗传算法优化的主循环 %进度条 wait_hand = waitbar(0,'run……', 'tag', 'TMWWaitbar');
while gen<ga_max
    %% 遗传算法选择
    FitnV=ranking(Value);%分配适应度值
    Chrom=select('rws',Chrom,FitnV,1);%选择
    Chrom=mutationGA(Chrom,popsize,PM,N,lb,ub);% 种群变异,单点变异
    Chrom=crossGA(Chrom,popsize,PC,N);% 种群交叉,单点交叉
    Value= decodingFun(Chrom,popsize);%解码染色体
    %% 计算最优
    [v1,index1]=min(Value);
    gen=gen+1;
    tracemat(gen,2)=mean(Value);
    %% 记录最优
    if gen==1
        bestChrom1=Chrom(index1,:);%记录最优染色体
        bestValue1=v1;%记录的最优值
    end
    if bestValue1>v1
        bestValue1=v1;%记录的最优值
        bestChrom1=Chrom(index1,:);
    end
    tracemat(gen,1)=bestValue1;% 保留最优
    waitbar(gen/ga_max,wait_hand);%每循环一次更新一次进步条
end
delete(wait_hand);%执行完后删除该进度条
disp('算法运行时间');
runtime1=toc
 
% 显示结果
disp('遗传算法优化得到的最优目标函数值');
bestValue1
disp('遗传算法优化得到的最优染色体');
bestChrom1
 
 
 
figure;
plot(tracemat(:,1),'r-','linewidth',1);
hold on;
plot(tracemat(:,2),'b-','linewidth',1);
legend({'种群最优值','种群均值'},'fontname','宋体');
xlabel('迭代次数','fontname','宋体');
ylabel('目标函数','fontname','宋体');
title('遗传算法优化','fontname','宋体');
 
x=bestChrom1;
[y,XY2,E]=myfun(x);
 
XY2
 
title1='结果';
drawnodes(XY,XY2,E,title1);
 
x2=x;
x2(8)=x2(8)+3;
[y,XY2,E]=myfun(x2);