> 和 >>> 详细分析

1、计算机二进制系统中最小单位bit

在计算机二进制系统中： bit (位) ：数据存储的最小单元。简记为b，也称为比特(bit)，每个二进制数字0或1就是一个位(bit)，其中，每 8bit = 1 byte(字节)；

再回顾Java 中的数据类型，如int数据类型 = 4个byte(字节)，而1 byte(字节) = 8 bit(位)；也就我们常说的int = 32位（说白了，在二进制系统中是以bit 作为数据存储单元的）。如下

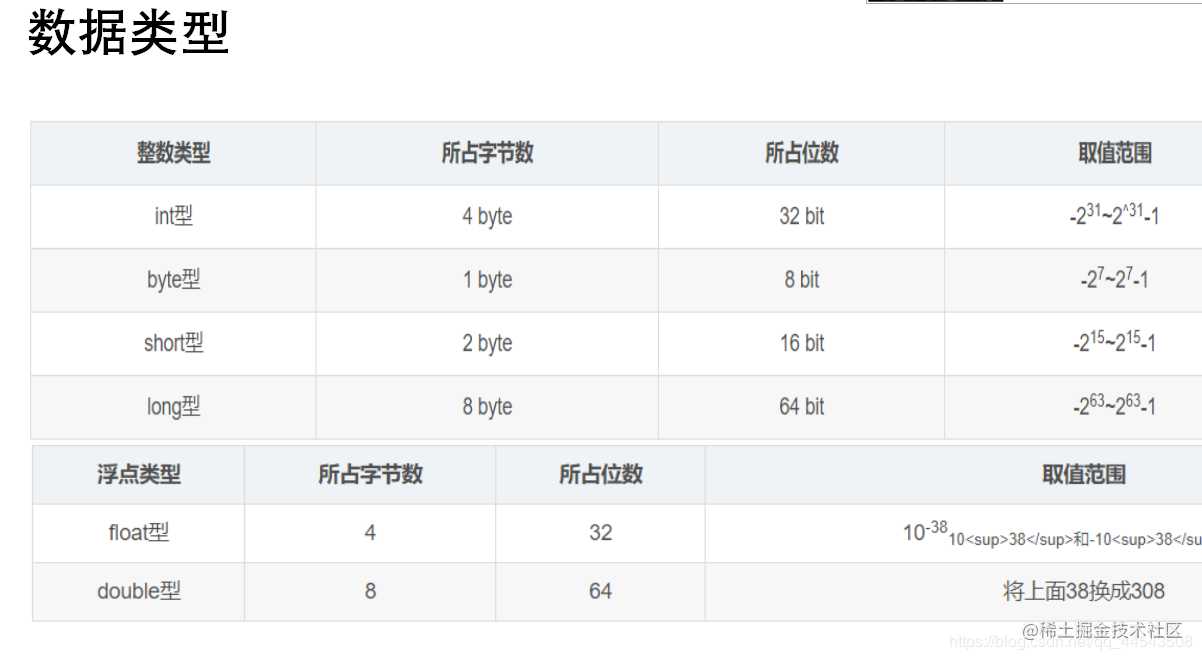
2、有符号数和无符号数

有符号数和无符号数简单的说就是分别对应正数和负数，在二进制系统中是以bit（位）来作为数据存储单元的，最高位（第一位）是符号位，正数符号位为“0” ，负数符号位为“1” 。

例子：

假设 int number = 1 ,那么number在计算机系统中将表示如下：

00000000 00000000 00000000 00000001

同理可得，number = -1 时，在二进制中表示如下：

10000000 00000000 00000000 00000001

注意：最高位（第一位）是符号位，因为是number值为1是一个正数，所以最高位为0；

3、二进制的原码、反码、补码

原码原码就是机器数，是加了一位符号位的二进制数(因为数值有正负之分)，正数符号位为0，负数符号位为1。

反码带符号位的原码乘除运算时结果正确，而在加减运算的时候就出现了问题，比如: 用十进制表示:1 + (-1) = 0, 但用二进制表示:

00000001 + 10000001 = 10000010,

将结果换算成十进制数也就是 -2。于是在原码的基础上发明了反码,用来解决这种问题。

补码虽然反码的出现解决了正负数的加减问题, 但却让0这个数字有了两种”形态”: “0”和”-0″, 但这是不合逻辑的,只应该有一个0,所以出现了补码。

对于有符号数而言：

1、正数的原码、反码、补码都一样； 2、负数的反码 = 它的原码符号位不变，其他位取反（取反的意思：0 换成 1 、 1 换成 0 ）； 3、负数的补码 = 它的反码 +1； 4、0的反码、补码都是0； 【特别注意】 1、在计算机运算的时候，都是以补码的方式来运算的。 2、二进制转为十进制，必须使用二进制的原码进行转换。

例子：

下面我们就使用“有符号数”来模拟一下，在计算机中是怎样运算的。

(1)正数相加：

例如：1+1 ，在计算机中运算如下：

1的原码为：

00000000 00000000 00000000 00000001

因为“正数的原码、反码、补码都一样”，所以，1的补码 = 1的原码，所以 1的补码+ 1的补码就等于：

00000000 00000000 00000000 00000001 + 00000000 00000000 00000000 00000001

00000000 00000000 00000000 00000010

00000000 00000000 00000000 00000010（转换为10进制） = 2

(2)正数相减：

例如：1 – 2，在计算机中运算如下：

在计算机中减运算其实是作为加运算来操作的，所以，1 – 2 = 1 + ( -2 )

第一步：把 1的补码找出来（因为正数的原码、反码、补码都一样，所以我们可通过原码直接获取补码）：

1的补码：

00000000 00000000 00000000 00000001

第二步：把-2的原码找出来：

-2的原码：

10000000 00000000 00000000 00000010

第三步：把-2的反码找出来：

-2的反码：

11111111 11111111 11111111 11111101

第三步：把-2的补码找出来：

-2的补码：

11111111 11111111 11111111 11111110

第四步：1的补码与-2的补码相加：

00000000 00000000 00000000 00000001 + 11111111 11111111 11111111 11111110

11111111 11111111 11111111 11111111

第五步：将计算结果的补码转换为原码，反其道而行之即可（如果想将二进制转换为十进制，必须得到二进制的原码）

补码：11111111 11111111 11111111 11111111

反码：11111111 11111111 11111111 11111110

原码：10000000 00000000 00000000 00000001

第六步：将计算结果的二进制原码转换为十进制

二进制原码：10000000 00000000 00000000 00000001 = 1*2^0 = -1

4、思考:java中为什么byte的取值范围是-128~127

java中byte占一个字节, 也就是8bit(位), 其中最高位是符号位, 剩下7位用来表示数值.若符号位为0, 则表示为正数,范围为00000000~01111111(补码形式)，也就是十进制的0-127. 若符号位为1, 则表示为负数, 范围为10000000~11111111(补码形式), -128~-1, 11111111转换为原码就是10000001,也就是-1。在补码中,为了避免存在”-0″,规定10000000为-128, 所以解释了byte的取值范围为什么是-128~127.

5、Java中的<< 和 >> 和 >>>

首先<< 和 >> 和 >>>是java中的位运算符，是针对二进制进行操作的。除了这些还有&、|、^、~、几个位操作符。不管是初始值是依照何种进制，都会换算成二进制进行位操作。这里主要讲解Java中的<< 和 >> 和 >>>。

<< 表示左移移，不分正负数，低位补0

注：以下数据类型默认为byte为8位，左移时不管正负，低位补0

正数：r = 20 << 2

20的二进制补码：0001 0100

向左移动两位后：0101 0000

结果：r = 80

负数：r = -20 << 2

-20 的二进制原码：1001 0100

-20 的二进制反码：1110 1011

-20 的二进制补码：1110 1100

左移两位后的补码：1011 0000

反码：1010 1111

原码：1101 0000

结果：r = -80

‘ >> ’表示右移，如果该数为正，则高位补0，若为负数，则高位补1；

注：以下数据类型默认为byte为8位

正数：r = 20 >> 2

20的二进制补码：0001 0100

向右移动两位后：0000 0101

结果：r = 5

负数：r = -20 >> 2

-20 的二进制原码：1001 0100

-20 的二进制反码：1110 1011

-20 的二进制补码：1110 1100

右移两位后的补码：1111 1011

反码：1111 1010

原码：1000 0101

结果：r = -5

‘ >>> ’ 表示无符号右移，也叫逻辑右移，即若该数为正，则高位补0，而若该数为负数，则右移后高位同样补0

注：以下数据类型默认为int 32位

正数： r = 20 >>> 2

的结果与 r = 20 >> 2 相同；

负数： r = -20 >>> 2

-20原码：10000000 00000000 00000000 00010100

反码：11111111 11111111 11111111 11101011

补码：11111111 11111111 11111111 11101100

右移：00111111 11111111 11111111 11111011

结果：r = 1073741819

最后，若有不足或者不正之处，欢迎指正批评，感激不尽！

欢迎各位关注我的公众号，里面有一些java学习资料和一大波java电子书籍，比如说周志明老师的深入java虚拟机、java编程思想、核心技术卷、大话设计模式、java并发编程实战…..都是java的圣经，不说了快上Tomcat车，咋们走！最主要的是一起探讨技术，向往技术，追求技术，说好了来了就是盆友喔…