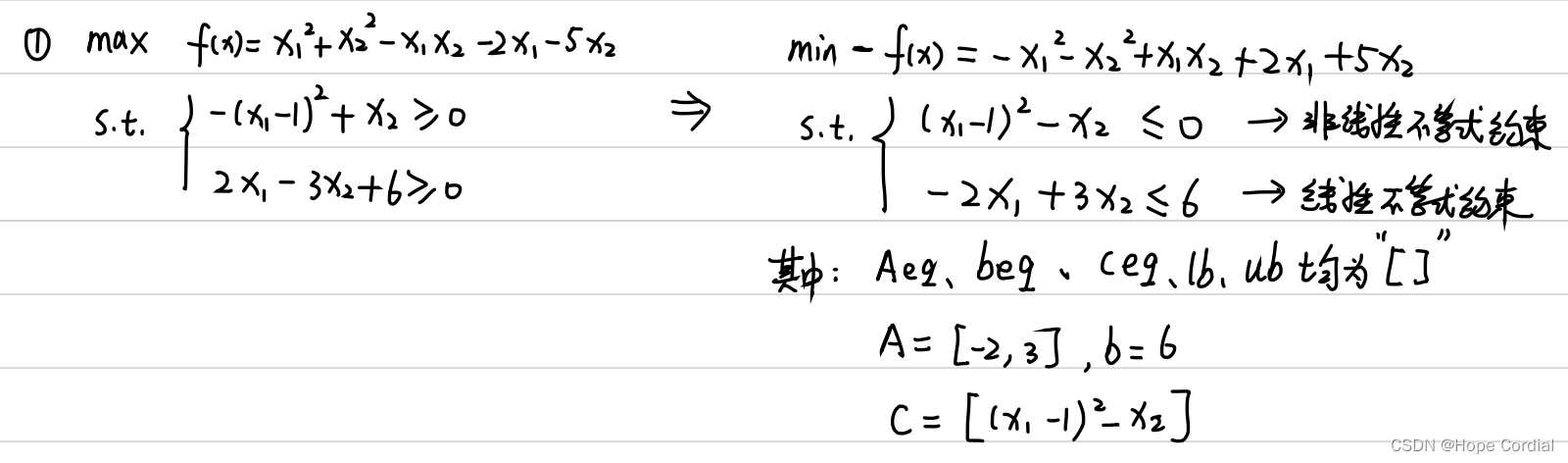前言

数学规划是运筹学的⼀个分⽀，其⽤来研究：在给定的条件下(约束条件),
如何按照某⼀衡量指标（目标函数）来寻求计划、管理⼯作中的最优⽅案 ，即求目标函数在⼀定约束条件下的极值问题。
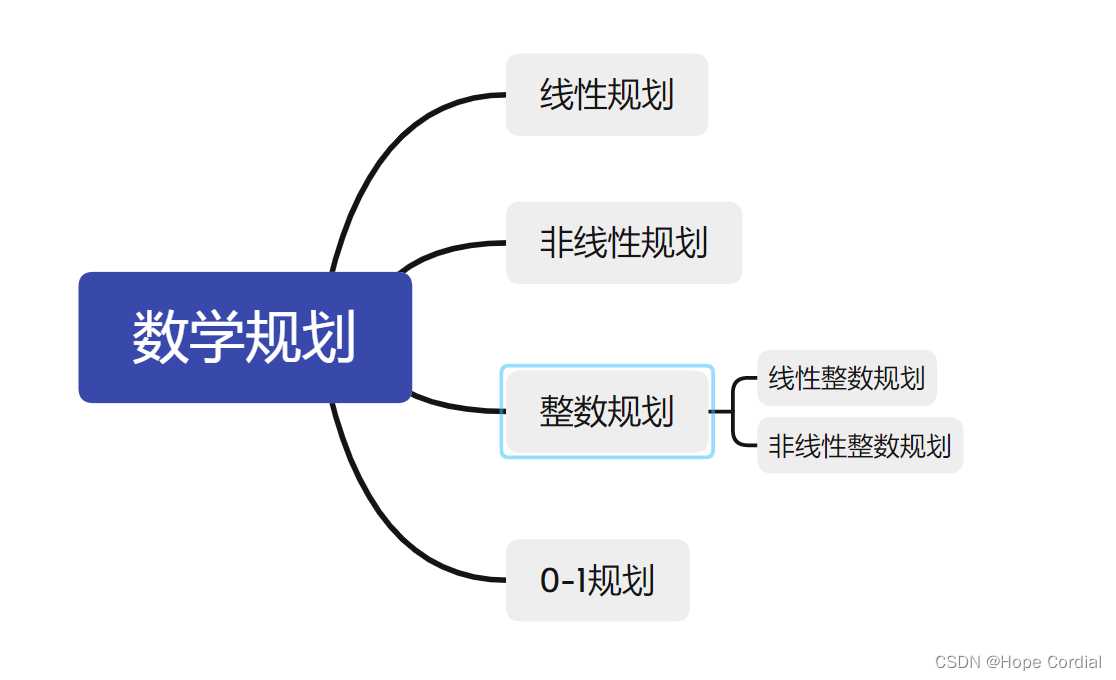
规划模型主要分为：线性规划问题、非线性规划问题、整数规划、最大最小化模型、多目标规划。

一、数学规划的一般形式

$$\{\begin{array}{l}\min \left(\text{或者}\max \right)Z=f\left(x\right)\\ s.t.g_i\left(x\right)\le 0,i=1,2,\dots ,m\left(\text{不等式约束}\right)\\ \left(\text{也有可能有等式约束、整数约束，或者两者皆有}\right)\end{array}$$
x:决策变量（一般有多个自变量）
f(x)：目标函数
约束条件：不等式约束、等式约束、整数约束

二、线性规划

1.MATLAB中线性规划的标准型

例子：

2.MATLAB求解线性规划的函数 —— linprog

三、非线性规划

1.MATLAB中非线性规划的标准型

例子：

2.Matlab求解非线性规划的函数 —— fmincon

四、整数规划

1.说明

2.Matlab线性整数规划求解 —— intlinprog

3.Matlab线性 0-1 规划求解

4.举例

五、最大最小化模型

1.模型的一般形式

2.模型的求解

六、多目标规划模型

1.求解思路

总结

暂无

今天的文章数学建模 —— 规划模型分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。