什么叫动态规划问题?
考虑一个场景:当你有去沙漠旅行,你有一个背包和一些物品,背包有最大承受重量,物品也有重量和价值,而物品种类很多,不可能全都装在背包里,如何去选取价值总量最高的物品组合呢?
物品价值表
| 物品名 | 价值 |
| water | 10 |
| book | 3 |
| food | 9 |
| jacket | 5 |
| camera | 6 |
物品重量表
| 物品名 | 重量 |
| water | 3kg |
| book | 1kg |
| food | 2kg |
| jacket | 2kg |
| camera | 1kg |
考虑使用贪婪算法,那就是什么价值高就优先拿什么,但有时这种近似解会不准,这时就要采用动态规划方法:从小问题入手,逐步解决大问题,可以帮助你在给定约束条件下找到最优解
首先定义一个表格,横坐标是背包重量,纵坐标是物品名称,填入值是当前物品,当前背包重量的最大价值:
| 物品/背包重量 | 1kg | 2kg | 3kg | 4kg | 5kg | 6kg |
| water | ||||||
| book | ||||||
| food | ||||||
| jacket | ||||||
| camera |
动态规划的解决方案就是把这张表填好,然后根据背包重量选择在该重量下最大价值所组成的物品
填入规则:每一行只能拿取当前行和之前行的物品
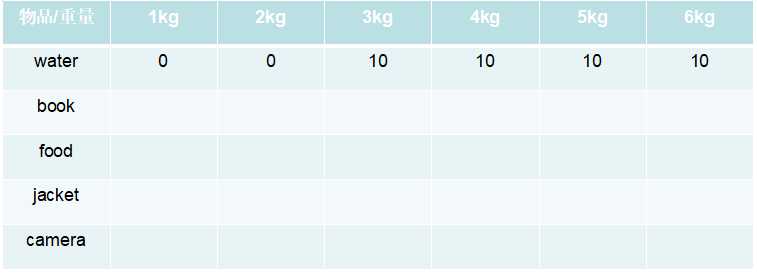
先看第一行water,这时只有water,没有之前的物品,而water的重量是3kg,那么在1kg,2kg的背包就装不下water,在3kg以上重量的背包就可以放入water,结果如下:
注:这时候只有水,没有其他的
现在再看第二行book,这时候可以拿的物品就有book和water,而book的重量是1kg
在1kg背包时可以放入book
2kg背包也只能放book(water放不下)
当3kg的背包时,这时候会面临选择,因为water的重量是3kg,可以放water,也可以放book,那么取价值最大的放进背包(water的价值是10,book是3)
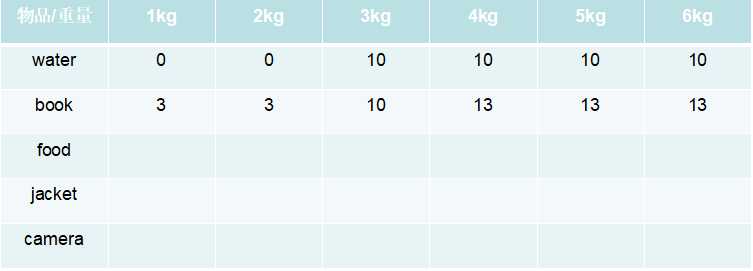
当4kg的背包时,water和book的总重正好是4kg,这时可以把这两个都放进去,所以第二行结果如下:
再看第三行,这时候可以拿water,book,food
在1kg背包时还是只能放下book
当2kg背包时多了个选项,因为food的重量是2kg,所以去价值最大的放在包里(food的价值是9)
3kg的时候的选择有:(1)放入water,(2)放入book,food,对比价值大小选择放入book和food,
4kg时根据价值最大原则,放入food和water
5kg时放入water和food
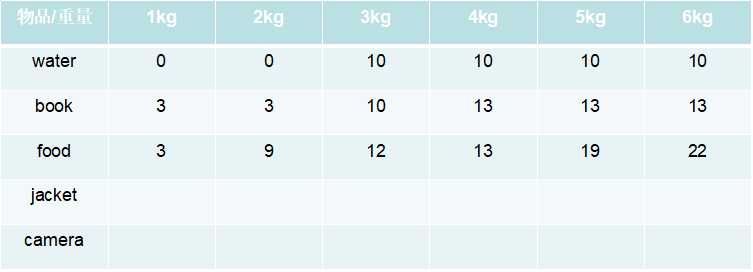
6kg是放入water,food,book刚好都放下了
结果为:
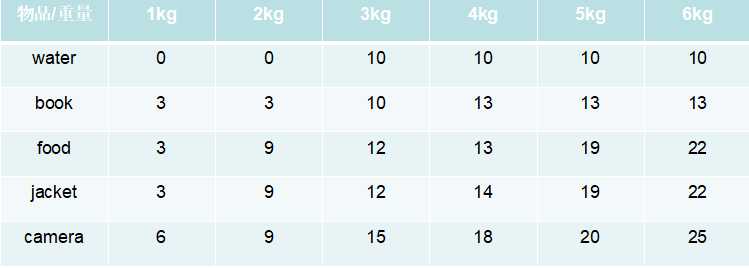
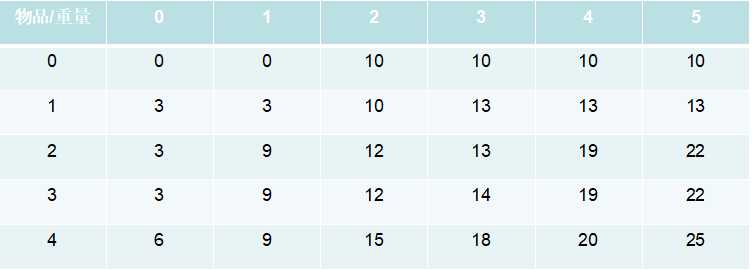
第四行和第五行也是采用这样的策略填入价值,最终结果为:
其实这里填的数字是有规律的:
现为方便说明把上面的图表转化为矩阵为:
那么填入的原则为:
table[i][j]= max(table[i-1][j],当前商品的价值+剩余空间价值(table[i-1][j-当前商品重量]))
注:如果处于特殊位置,如table[0][0]单元格,没有table[i-1][j]那么就是0
例:
table[3][4]=max(table[2][4],worth(jacket)+table[2][4-weight(jacket)])
=max(19,5+10)
=19
与之前一步步推算的结果一致
又例:
table[0][4]=max(table[0-1][4],worth(water)+table[0-1][4-weight(water)] (因为是第一行,所以有些数据是空的,定为0)
=max(0,10+0)
=10
同样与之前推算的结果一致
那既然有逻辑有公式,那就可以写代码了:
python版本3.6
使用库:numpy
#动态规划
import numpy as np
#定义重量
weight={}
weight["water"]=3
weight["book"]=1
weight["food"]=2
weight["jacket"]=2
weight["camera"]=1
#定义价值
worth={}
worth["water"]=10
worth["book"]=3
worth["food"]=9
worth["jacket"]=5
worth["camera"]=6
#存放行标对应的物品名:
table_name={}
table_name[0]="water"
table_name[1]="book"
table_name[2]="food"
table_name[3]="jacket"
table_name[4]="camera"
#创建矩阵,用来保存价值表
table=np.zeros((len(weight),6))
#创建矩阵,用来保存每个单元格中的价值是如何得到的(物品名)
table_class=np.zeros((len(weight), 6), dtype=np.dtype((np.str_,500)))
for i in range(0,len(weight)):
for j in range(0,6):
# 获取重量
this_weight = weight[table_name[i]]
# 获得价值
this_worth = worth[table_name[i]]
#获取上一个单元格 (i-1,j)的值
if(i>0):
before_worth=table[i-1,j]
#获取(i-1,j-重量)
temp=0
if(this_weight<=j):
temp=table[i-1,j-this_weight]
#(i-1,j-this_weight)+求当前商品价值
#判断this_worth能不能用,即重量有没有超标,如果重量超标了是不能加的
synthesize_worth=0
if(this_weight-1<=j):
synthesize_worth=this_worth+temp
#与上一个单元格比较,哪个大写入哪个
if(synthesize_worth>before_worth):
table[i,j]=synthesize_worth
if(temp==0):
#他自己就超过了
table_class[i][j] = table_name[i]
else:
# 他自己和(i-1,j-this_weight)
table_class[i][j] = table_name[i] + "," + table_class[i - 1][j - this_weight]
else:
table[i,j]=before_worth
table_class[i][j]=table_class[i-1][j]
else:
#没有(i-1,j)那更没有(i-1,j-重量),就等于当前商品价值,或者重量不够,是0
if(this_weight-1<=j):
table[i,j]=this_worth
table_class[i][j]=table_name[i]
print(table)
print("--------------------------------------")
print(table_class)最终结果:
如图红框部分可知:当背包重量为6kg是,选择camera,food,water可使价值最大
今天的文章动态规划python实现分享到此就结束了,感谢您的阅读,如果确实帮到您,您可以动动手指转发给其他人。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/26426.html