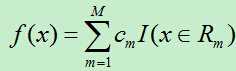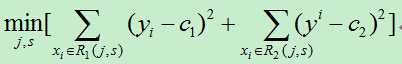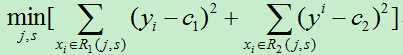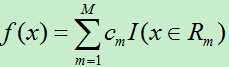CART回归树算法过程

CART决策树算法是一种分类及回归树算法，既可以用于分类，也可以用于回归。但是在李航老师的《统计学习方法》一书中，并没有详细介绍回归树，更多的是介绍分类树，所以有必要对CART回归树进行简单介绍，有利于对CART树用于回归的操作，因为后续GBDT算法也是在CART回归树的基础上进行的，所以深入理解CART回归树非常重要。

回归树：使用平方误差最小准则

训练集为：D={(x1,y1), (x2,y2), …, (xn,yn)}。

输出Y为连续变量，将输入划分为M个区域，分别为R1,R2,…,RM,每个区域的输出值分别为：c1,c2,…,cm则回归树模型可表示为：

则平方误差为：

假如使用特征j的取值s来将输入空间划分为两个区域，分别为：

我们需要最小化损失函数，即：

其中c1,c2分别为R1,R2区间内的输出平均值。（此处与统计学习课本上的公式有所不同，在课本中里面的c1,c2都需要取最小值，但是，在确定的区间中，当c1,c2取区间输出值的平均值时其平方会达到最小，为简单起见，故而在此直接使用区间的输出均值。）

为了使平方误差最小，我们需要依次对每个特征的每个取值进行遍历，计算出当前每一个可能的切分点的误差，最后选择切分误差最小的点将输入空间切分为两个部分，然后递归上述步骤，直到切分结束。此方法切分的树称为最小二乘回归树。

最小二乘回归树生成算法：

1）依次遍历每个特征j，以及该特征的每个取值s，计算每个切分点（j,s）的损失函数，选择损失函数最小的切分点。

2）使用上步得到的切分点将当前的输入空间划分为两个部分

3）然后将被划分后的两个部分再次计算切分点，依次类推，直到不能继续划分。

4）最后将输入空间划分为M个区域R1,R2,…,RM,生成的决策树为：

其中cm为所在区域的输出值的平均。

总结：此方法的复杂度较高，尤其在每次寻找切分点时，需要遍历当前所有特征的所有可能取值，假如总共有F个特征，每个特征有N个取值，生成的决策树有S个内部节点，则该算法的时间复杂度为：O(F*N*S)。

今天的文章CART回归树算法过程分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。