原理概述

snake模型将图像分割问题转换为求解能量泛函最小值的问题。主要思路是构造能量函数进行迭代后，轮廓曲线由初始位置逐渐向使能量函数最小（局部极小）的图像边缘逼近，最终分割出目标。

曲线理论

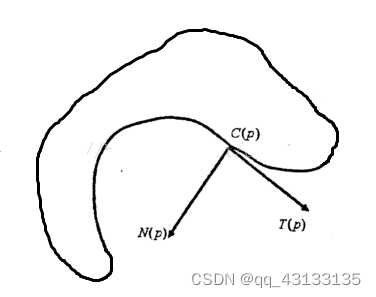
假设一条光滑封闭曲线 C=$C(p)$，则在点p处有切向量$T(p)$和法向量$N(p)$相互垂直：

且有$\frac{dC}{dp}=T(p)$, $\frac{d^{2}C}{d{p}^2}=kN(p)$, 其中k是曲率。曲线在p处有近似的二阶展开：
$C(p)=C(p_0)+k_1\frac{dC}{d{p}_0}+k_2\frac{d^{2}C}{d{p}_0^2}$
即:
$C(p)=C(p_0)+\alpha T(p_0)+\beta N(P_0)$
其中法向量决定了曲线的弯曲方向，

算法原理

首先需要人为在图像上给出一组用于控制曲线形状的控制点：$v(s)=[x,y]$，这些首尾相连的点构成一个封闭的轮廓线。v是当前最小能量的位置，在迭代过程中，v会移向下一次能量最小的v’位置。

Snake曲线的能量函数表示为：
$E_{snake}=E_{int}+E_{ext}$

$E_{int}$是内部能量函数，依赖于轮廓形状：

$E_{int}=\int \frac{1}{2}\times (\alpha (s)\mid c^{\prime }(s){\mid }^2+\beta (s)\mid c^{\prime \prime }(s){\mid }^2)ds$
由之前的曲线理论我们知道，式中两项的作用
法向量：推动轮廓形状的改变，决定轮廓平滑度
切向量：保持轮廓点的间离

$E_{ext}$是外部能量函数，依赖于图像的性质：

$E_{ext}=-(E_{mag}+E_{ext})$
$E_{image}$:灰度能量，决定将轮廓吸引到 暗/亮 的区域
$E_{mag}$:梯度能量，将图像推向边缘特征

今天的文章主动轮廓模型snake分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。