碎纸片的拼接复原

摘  要

对重要文件的拼接复原，传统上都由人工完成，拼接准确率虽然高但是效率很低。本文旨在建立模型，利用计算机编程加少量的人工干预实现碎纸片的拼接复原。

针对问题1，由于对任意一个字符来讲，笔画是连续的，所以对于一般情况，即使文字被切开，两边的像素还是有联系的，是呈现离散性渐变的。针对此特征，建立了文字连续性模型来求解该问题。而又因为被切开的两边碎片边缘灰度是具有高相关性的，所以，又建立了向量相关模型来求解进行图片拼接。用两种模型分别求解，都得到了对附件一和附件二的正确拼接结果。

针对问题2，可以采用第一问的模型，先进行全局搜索，找出每个碎片最相似的右侧邻近碎片，拼接出每一行的图片，再利用向量相关性进行横向拼接，得到拼接结果。但是，由于纸片同时被横向与纵向切割，碎片小，数量多，碎片之间的信息量不够，容易造成误判。所以建立向量投影分类模型，首先将可能处于同一行的碎片用模糊C均值(FCM)聚类方法分到同一类。对于汉字或英文的缺行碎片（碎片中只有一行或者两行字），利用掩码补充模型将投影中缺失的行用掩码补齐，然后再放入分类。分类完成后，将每一类中的碎片进行横向排序拼接。每一类横向拼接完成后，从而拼接成完整图片。对于不能正确拼接的部分，采取了多种人工干预的策略，最终得到正确的拼接结果。

针对问题3，由于附件中的碎片分为正反两面，所以可以建立组合匹配模型将碎片首先将正反面碎片的灰度矩阵上下拼接，每张碎片的拼接方案有两种（灰度矩阵a放在左右镜像处理后的b上或灰度矩阵b放在左右镜像处理后的a上）。拼接过后，边缘灰度向量信息会增加为原来的两倍，这时利用问题二中的全局搜索模型用向量相关性的方法进行匹配拼接。拼接出所有行后，将每一行的下半部分矩阵切割放在上半部分的右边，又可增加横向拼接时的边缘信息，然后各行再次利用向量相关性的方法进行横向拼接，最终得到结果图，但是仍然存在较多的碎片不能正确匹配，需要人工干预。

由于碎片在切割时的随机性，使得机器自动拼接存在一定的难度，因此，采取恰当的人工干预的措施，是保证正确拼接的必要手段。

 

 

关键词：文字连续性  匹配  FCM聚类方法 掩码补充模型  向量投影分类模型

一．问题背景及重述

破碎文件的拼接在司法物证复原、历史文献修复以及军事情报获取等领域都有着重要的应用。传统上，拼接复原工作需由人工完成，准确率较高，但效率很低。特别是当碎片数量巨大，人工拼接很难在短时间内完成任务。但如果借助计算机技术，开发出碎纸片的自动拼接技术，提高拼接复原效率将会大大提高。

问题1：给定的来自同一页印刷文字文件的碎纸机破碎纸片（仅纵切），建立碎纸片拼接复原模型和算法，并且拼接复原附件1和附件2给出的中、英文各一页文件的碎片数据。

问题2： 对于碎纸机既纵切又横切的情形，设计碎纸片拼接复原模型和算法，并针对附件3和附件4给出的中、英文各一页文件的碎片数据进行拼接复原。

问题3：从现实情形出发，还可能有双面打印文件的碎纸片拼接复原问题需要解决。附件5给出了一页英文印刷文字双面打印文件的碎片数据。设计相应的碎纸片拼接复原模型与算法，并就附件5的碎片数据给出拼接复原结果。

二．模型假设

1、不计碎纸片边缘的磨损，没有边缘像素损耗；

2、假设纸张垂直放入碎纸机即每张小碎纸片都是规则矩形；

3、图片中的文字像素没有任何断点；

4、图像上没有任何噪声或污点造成像素干扰。

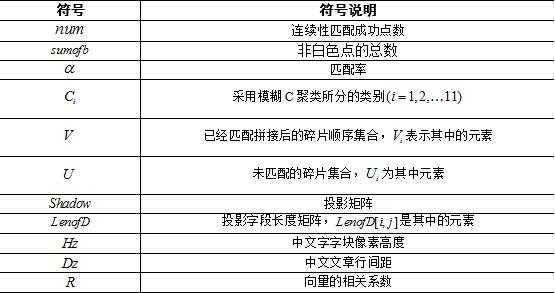
三．变量说明

  

 

四．模型准备与问题分析

针对题目中附件所给的图片信息，我们学习准备了图像的处理方法[1]、模式匹配方法[2]和图像拼接方法[3,4]。将图片批处理成范围值0-255之间的灰度矩阵（纯黑为0，纯白为255，数字越大，颜色越亮）。

问题一中的附件图片，碎片数据较少，每一张碎片都比较大，那么相应的灰度矩阵中包含的信息就比较多，处理起来相对容易。而且仔细观察，分别只有一张图片的最左端和最右端边缘是没有文字的。由于完整纸片切开后，边缘处仍然是有联系的。所以可以提取图像边缘的灰度信息，首先找出第一张图片，然后利用图片的边缘信息找出下一张图片与之拼接。

问题二中，给出的图片碎片比较小，只有180*72像素，图像信息以及边缘信息都比较少。而且，由于既横切又纵切，图片的顺序被打乱，无法直接拼接。因此，首先得将这些碎片分类，将同一行的图片归在同一类中，然后将归类后的图片进行横向排序，拼接出这一行的图片碎片，因为有些碎片包含的边缘信息过少，可能无法分类或者成功排序，这时进行人工干预。每一行图片按排序拼接后，即可将问题转化为第一问的问题进行纵向拼接，最终得到结果。

问题三中附件五的碎片与问题二中附件四的类似，都是英文小碎片，但是正反面被打乱。虽然正反面一开始无法识别，但是某一张图的正面与另一张正面横向投影对齐，反面的横向投影也就会对齐。所以我们可以利用a面和b面的矩阵上下组合，变成一个大的单面图片，一方面增加了拼接的信息量，同时又将问题转化为第二问中类似的问题，利用第二问的模型即可找出双面碎片的拼接结果。

五．模型建立与求解

5.1   问题一的求解

5.1.1 基于文字连续性模型的碎片拼接

首先，对问题1的分析可知，该问题为一个图像处理问题。根据字的特征，我们知道笔画是连续的，图片放大之后我们也能看到有字的部分图像偏暗，由字中间向边缘，慢慢变亮直至超过字范围而变成白色。我们利用这一点，建立文字连续性模型来处理拼接问题。

       

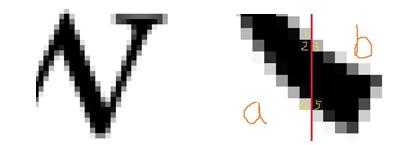
（a）                                                                  （b）        

图1：点阵字体的锯齿现象

由字体放大图1(a)可以看出笔画周边的锯齿，每一个锯齿方块就是一个像素，范围大小在255以下。切割后的图像，这些锯齿也会分开。但是，虽然像素分开了，由于汉字字体或者英文字体大部分是连体的，所以这些碎片的图像灰度信息会有一定的相关性或者说是连续性。

如图1(b)，假如图片像素按照红线所示切开分为a，b两块。可以看到红线左右两边的像素块大都是相连的，最理想的情况就是如同像素块2，3或者4，5在同一位置直接对应，这种情况就可以认为这两个像素块匹配，匹配数num加1。但是，也有可能出现像素块1这样的情况，与之对应的位置没有像素块，但是下方或者上方有像素块，由于这些像素的连续性，所以也认为像素1得到匹配，num=num+1。

读取所有图片，由于纸张有页边距，若某一张碎片为完整纸片上的最左一张，则其图像左侧必定全为白色，即灰度值的前几列为255，通过这种方法，能很快找到第一张碎片，将其放入集合中，记为。

找到第一张碎片后，用第一张碎片的右边缘去和中所有碎片的左边缘进行匹配。由于白色点太多，匹配成功数会很大，影响结果。所以，我们只选取非白色点进行匹配，匹配过程中，非白色点的总数记为sumofb，每选取边缘非白色点匹配一次，sumofb=sumofb+1。

匹配率[3]的计算方法为：

                         （1）

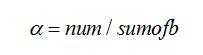
求得第一张碎片的右边缘和集合中每张碎片左边缘的匹配率后，将所得的匹配率对比，选取匹配率最高的那张碎片，将其放入集合中，记为（i为碎片的排列顺序），将右边缘像素去和中剩余碎片的左边缘像素进行匹配，重复此类操作，直到中没有碎片，最终得到排序结果即为碎片的拼接方案。计算所得集合中与的最大匹配率如表1所示。

 

表1：附件一中中文字符碎片拼接顺序及匹配情况：

 

表2：附件一中英文字符碎片拼接顺序及匹配情况：

 

5.1.2  基于向量相关性的碎片拼接

     提取碎片边缘向量，选出第一张图片后，计算右边缘向量与集合中的每一张碎片左边缘向量的相关系数[5]：

                                                    （2）

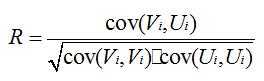
将所得的对比，选出相关系数最最大的，放入集合中。再用选出的碎片右边缘向量与中剩余碎片匹配，重复此操作，直到中没有碎片，最终得到排序结果即为碎片的拼接方案。计算求得集合中与的相关系数为：

表3：附件二中中文字符碎片拼接顺序及匹配情况：

 

5．2  问题二的求解

问题二中所给附件三、四都是小碎片，宽度为72像素，与第一问中的一致，但是高度只有180像素，为第一问碎片的1/11，所以左右边缘的灰度信息较少，容易造成误判。

5.2.1 模型1 建立全局搜索的碎片拼接模型

由问题一的求解可以看出，利用向量相关模型或者文字连续性模型可以不必区分碎片的文字语言。所以对于问题二，可以建立全局搜索模型，同时利用第一问中的向量相关分析来进行碎片拼接。全局搜索模型算法如下：

Step 1：根据页边距找出11张处于纸片第一列的碎纸片，记为集合。取其中一张记为，放入；

Step 2：我们从存放于U的所有纸片中任取一张碎纸片与进行向量匹配，记录下匹配的相关系数，取相关系数最大的那张图片作为的下一张纸片，记为,以此法依次匹配得到后面的18张图片（最后一张同样存在页边距）；对于得到的这样一条横串，我们记为

Step 3：从上面的集合中再任取一张图片记为，重复step2；

Step 4：当，我们根据问题1中的方法对进行拼接，即可得到整张纸片原图。

5.2.2模型2 基于向量投影分类的碎片拼接模型

但是由于附件三和四中都给出了209张碎片，如果进行全局搜索的话，时间复杂度，计算量十分庞大。所以为了减少计算时间，我们首先根据碎片中行距的位置对碎片进行预分类，将同一行的碎片分在一类，再对同一类中的碎片利用第一文的方法进行排序。

由于中英文文字在像素图片中的显示形式不一样，所以我们通过这两种文字显示的不同特征来用两种投影方式来进行分类排序。

1、 中文字的碎片拼接

（1）中文字碎片向量投影

针对中文字像素图片，可以利用中文字是方块字的特点首先建立向量投影匹配分组模型。附件3中所给11×19共209张图片，可以拼成完整的一篇文章，那么同一行的文字被切开后，字体仍然在相对的同一高度上。

图2 碎片投影

所以，利用这一特征，我们可以首先利用掩码补充法将图片中文字的行间距找出来，利用不同行的文字中行间距在图片中的高度不通，对碎片经行预分类，将同一行的碎片分在一类总，然后利用第一问中的方法对行内小块经行排序。掩码补充法的具体做法是：将像素矩阵水平投影，如图2，设当某一像素行都为白色255时，投影值只为0，当一像素行有小于255的像素块时，此行投影为1。最终，209张图片生成209列的投影矩阵Shadow。

（2）字符的填补

投影碎片的灰度信息，由于中文字中有上下结构的字，如，附件三中的“010.bmp”碎片中的“翁”字，中间有一小段的投影出现缺失。这时，由于投影向量中全白色段的长度很小（甚至可能为1个像素点），并且上下两字段的长度加起来接近一个中文字符块的高度时，我们将此段的投影向量填充为1，似得其投影矩阵具有连续性。

 

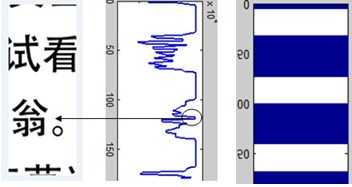
图3 字符缺损补充

（3） 字块的填补

利用掩码补充模型补充缺行碎片。在投影过程中，会遇到缺行的图片，这种缺行的图片大致分为三种：

                   

     图4 掩码补充时的特殊情况

如图4所示，有上部缺行，中部缺行和底部缺行。如果出现这样的情况，因为若全为白色的像素行过多，就有可能匹配不到分组。所以我们建立掩码补充模型，补充缺失的文字像素投影行，将缺失的文字像素投影段都补充为1，每一列的投影矩阵都叫做“投影编码”。

首先，我们将缺失投影行的图片搜寻出来，由于缺失一个字段，那么这些图片的向量投影值为1的连续段就会小于3，只有两段甚至是一段。利用这个方法，我们成功找出了缺失字段的图片，分别是第5 9 15 17 22 2628 33 41 61 67 71 72 75 86 90 94 102 107 109 110 111 114 115 118 120 124 126140 141 146 147 151 153 154 155 156 158 166 167 174 182 185 186 188 195 197 198205 206 208共51张（此数列的值比实际图片编号大一，如，第五张对应附件三中的004号图片）图片。

然后，我们将这些缺损字段的图片投影数据进行整合，计算每一段全白色段和非全白色段的段长（例如投影编码为00000011111100011，就记为6，6，3，2）并存入段长矩阵中，为了以后处理方便，我们都以全白色段的段长值开头，若起始为非纯白色段，则在此段长前加一0值，作为开头的全白色段长。

经过投影后的统计，一个中文字的高度Hz大约为41-42像素，而两行中文字之间的间距Dz大约为26-28像素。首先我们考虑上部缺行的图片，由于我们规定了段长矩阵中的第一列都为全白色段的长度，所以当第一列的值LenofD[i,1]大于间距Dz时，表示这张图片上部是有缺损的。然后根据上部缺损的不同长度段长LenofD[i,1]，将LenofD[i,1]分割成几个段长（这些段长为全白色段与非全白色段间隔表示），放在矩阵head中，用分割后的段长head取代LenofD[i,1]。

        （3）

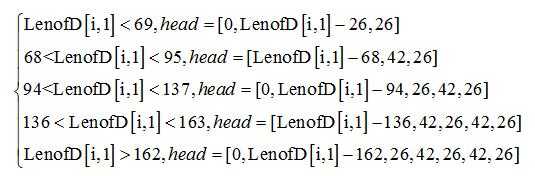
对于中部缺行的图片我们也采取类似的方案进行处理。对于图片中间部分的全白色段段长LenofD[i,mid],因为中部缺损肯定的是缺[非全白色段，全白色段，非全白色段]或者是[非全白色段，全白色段，非全白色段，全白色段，非全白色段]，只有两种情况，所以当LenofD[i,mid]大于（2×Dz+Hz）时：

     （4）

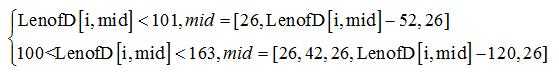
用mid矩阵取代LenofD[i,mid]。

最后一种底部缺行的处理方案也与上部缺行的类似。如果图片底部的LenofD[i,bom]大于间距Dz，就将LenofD[i,bom]分解成小块段长：

   （5）

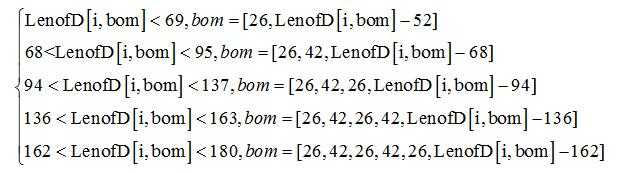
用bom矩阵取代LenofD[i,bom]。

将补充好的段长矩阵LenofDnew，重新按照段长和全白色段，非全白色段间隔排列的规则还原出新的投影矩阵Shadownew，在Shadownew中的原先缺行图片的缺失段都会被赋值1，这些补充后值为1的段就称作“掩码”。补充掩码后的投影急诊对应的图片，就相当于在缺行的那一段，补充了一个高度Hz的字段，效果如图5：

图5 掩码遮盖

 （4）用FCM聚类方法将碎片分类

将这些覆盖掩码后的投影矩阵Shadownew用模糊C均值(FCM)聚类方法^[2]进行分类，根据投影矩阵中的投影编码一共分为11类碎片。每一类所包含的图片序号为（序号比实际编号大一）：

表4：FCM预分类结果

C1	6     11    30    38    45    49    56    60    65    76    93    99    105  112  172  173  181  202  207
C2	7     20    21    37    53    62    64    68    70    73    79    80    97    100  117  132  163  164  178
C3	3     12    23    29    50    55    58    66    92    96    119  130  142  144  179  187  189  191  193
C4	9     10    25    26    36    39    47    75    82    89    104  106  123  131  149  162  168  190  194
C5	1     8     33    46    54    57    69    71    94    127  138  139  154  159  167  175  176  197  209
C6	17    22    67    107  110  111  140  146  151  158  174  182  185  188  198  205
C7	35    43    44    48    59    78    85    91    95    98    113  122  125  128  137  145  150  165  184
C8	4     13    15    32    40    52    74    83    108  116  129  135  136  160  161  170  177  200  204
C9	14    16    18    28    34    72    81    84    86    133  134  153  157  166  171  183  199  201  203  206
C10	2     19    24    27    31    42    51    63    77    87    88    101  121  143  148  169  180  192  196
C11	5  41  61     90    102  103  109  114  115  118  120  124  126  141  147  152  155  156  186  195 208

分类后C6中只有16张图片（少3张），C9中有20张（多1张），C11中有21张（多2张）。

（5）将分类好的碎片逐类横向拼接

分类完毕之后，继续利用向量相关模型进行横向拼接，拼接好同一类的一行之后，观察是否有拼接出错碎片。此时，由于程序对有些碎片无法正确匹配，必须进行人工干预，根据语义和偏旁部首进行手工拼接。

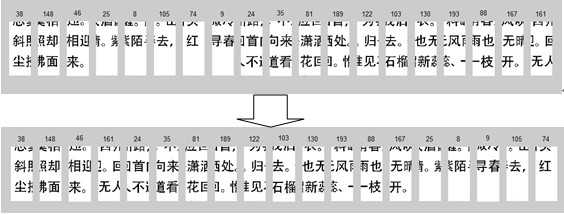
图6 人工干预前后比较

如图6，第46张与第25张碎片匹配出错，因为“迎”和“晴”都切在了竖线上，所以相关系数会很大，这是第一类典型的出错原因：边缘字形相近；第74张与第9张匹配出错，因为第74张碎片的右端边缘没有任何中文字符，造成正确无法计算相关系数，这是第二类出错原因：碎片边缘没有任何字符灰度信息。

人工干预时，根据中文字的特征，以及上下文的语义，我们进行手动调整错误的图片的位置，将此行拼成正确图片。

当每一个分类都成功拼接出正确图片行后，将这11个分类用在纵向进行拼接。纵向拼接成功后，在用向量相关模型进行横向拼接，最终得到正确结果：

表5：附件三的拼接结果

 

2、英文字的碎片拼接

（1）英文字碎片向量投影

对于英文字母，我们可以利用英文字母“四线三格”的书写格式，如图7所示：

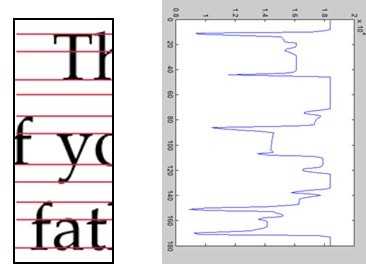
图7 英文字符“四线三格”表示

这种书写格式我们也可以通过碎片灰度矩阵的每行灰度值的和表示成折线图，从中图7

观察出来。每当那一行的值变化比较剧烈时，那一行一般情况下总是四线中的某一线。

通过多次分析得出相邻两条直线之间的距离，大致分别为(12,20,15,25),之后制作模板，把每一个碎片与模板比较。

通过寻找每一个碎片起始直线位置，与模板对应寻找可以匹配的个数，通过循环找出与模板匹配率最高的模式。根据匹配的模式，从起始位置对碎片根据此模式的间距向上向下添加直线，完成直线填补工作。

之后，通过模糊C均值(FCM)聚类方法进行分类，根据补齐直线投影矩阵分出11类，由于分类方法的模糊性特征，造成分出的类别误差相对较大（如下），在之后运用相关性函数匹配时造成了很大的错误，在人工干预时大大增加了工作量。

表6：英文碎片分类结果

C1	7     15    18    24    48    55    61    62    63    69    71    85    91    92    97    100  101  102  104  123 138  147  149  157  173  175  186  196  197  199  209
C2	27    29    34    143  163  170
C3	3     5     12    22    33    40    65    66    68    76    105  107  113  120  137  148  150  155  180  181 185  190  191  192  193  198  205
C4	8     50    119  134  169
C5	10    11    17    20    45    57    58    67    72    83    84    93    94    106  122  127  135  142  146  153 158  172  177  183  184  195  203  206
C6	19    23    28    35    36    43    56    75    89    111  115  152  156  166  168
C7	16    21    37    42    44    46    74    77    78    80    103  109  117  124  136  141  144  162  174  200 208
C8	1     2     49    51    53    54    64    73    82    86    88    90    98    116  121  125  126  129  130  132 139  140  154  160  161  176  178  188  194  201
C9	4     6     14    25    31    38    41    47    52    59    108  112  114  118  128  131  133  145  151  159 164  179  187  189  202  207
C10	13    32    39    60    70    79    95    96    99  165  167  204
C11	9     26    30    81    87    110  171  182

尽管直线修补后误差依然不小，相比于直接模糊C均值(FCM)聚类方法分类，大大提高了成功率，所以可以根据英文字书写格式的这种特征来进行向量投影。

表7：附件四的拼接顺序

根据不同的文字特征，对中英文碎片采取了不同的数学模型，汉字属于方块字，有明显的笔画连续性，字宽、字高，通过对方块字字块的判断可以比较好的判断匹配率；英文有明显的四线三格模式，通过直线寻找可以很好地把英文特征识别，提高匹配率。

5.3问题三的求解

5.3.1 基于组合匹配模型的双面碎片拼接

针对第三问附件中碎片的正反面，若某一碎片正面与另一碎片正面能够匹配，那么这两张图片的反面就是匹配的。利用这一特性，我们可以建立组合匹配模型。

将碎片图像信息转化为灰度矩阵，将每张图片的a，b面所对应的灰度矩阵上下拼接，每张碎片的拼接方案有两种（灰度矩阵a放在左右镜像处理后的b上或灰度矩阵b放在左右镜像处理后的a上），效果如图8所示：

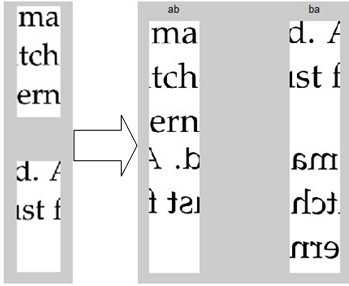
图8 拼接方案

通过拼接大大增加碎片的信息量，在接下来的模式匹配寻找，行列拼接时提高了成功率。

拼接之后，延用第二问的全局搜索模型。首先，搜索碎片的行首、行尾放到两个数组中，并把行首、行尾为之标记；接着，全文搜索，运用相关系数函数匹配，寻找出与之匹配率最高的碎片，放进一个集合中。

由于灰度矩阵的相似性，匹配时出现错误，形成一段一段拼接好的碎片图像，观察每一行用肉眼可以看出的错误的位置，并进行调整，最后，把每一行的碎片拼接完成。每一行拼接好之后，假设a面为正面，b面为反面，把b面的灰度矩阵连接到a面后面，形成Z（a，b）灰度矩阵；如果b为正面，a为反面，形成Z（b，a）灰度矩阵。

把每一行的灰度矩阵，之后把灰度矩阵进行转置，运用第一问的碎片相关性方法对灰度矩阵进行匹配，最后得出正确结果：

表8：附件五碎片正面拼接顺序

表9：附件五碎片反面拼接顺序

六．模型结果的分析与检验

6.1 连续性模型的实验分析检验

利用文字连续性模型，最终成功将附件一和附件二的长条型中英文字体碎片很好的拼接起来了，拼接后的文章语意通顺，说明结果正确。由于问题一中的纵向切割，使得形成的边缘处除了第一张和最后一张外，其余碎片没有完全空白的情况，这给我们寻找第一张碎片带来了很大的便利。这种先找出第一张碎片，再继续拼接后续碎片的方法。可以大大简化边缘匹配的过程。

经过程序实验论证，针对问题一的中英文碎片拼接，拼接后的正确率为100%。

这种连续性模型可以很好的拼接出边缘所含信息较多的碎片。但如果对于边缘只含有少量文字或者与其他碎片含有相似字形较多的碎片，就会产生误差。

所以这种模型适用于边缘信息较多的碎片拼接。

6.2  全局搜索模型以及向量投影分组模型的分析检验

问题二中所给附件三、四都是小碎片，宽度为72像素，与第一问中的一致，但是高度只有180像素，为第一问碎片的1/11，所以左右边缘的像素信息也只为附件一和二的1/11,如果实用文全局搜索模型利用向量相关性的方法来拼接碎片的时间复杂度。

而如果使用向量投影分组模型，把每一行有黑点的情况投影到一个数组中，组成以一个180*209的数组，之后运用聚类分析方法分出11类，分类时由于空白处造成分类误差，运用相关系数函数匹配判断时出现匹配错误后，运用人工干预，分为11类。然后进行横向匹配，此时的时间复杂度只为。此模型能节约大量运算时间并且能较好得适应边缘特征并不明显的时候，但由于分类的误差，造成最后匹配时出现了错误，需要人工干预，增加了工作量。

6.3  组合匹配模型的分析检验

通过图片的组合拼接，把碎片的信息量进行扩充，增大信息量，图片特征，在下面的对每一行的分类，每一列的匹配拼接提高了成功率。并通过反面对正面的检测分析，可以更好的避免误差，减少人工干预的次数，减少了工作量。但由于使用的是全局搜索模型，在时间复杂度，耗时较多。

图9附件五碎片横向拼接

根据碎片拼接图片可以看出，有碎片拼接错误，主要缘由是匹配函数的选取，相关性的匹配，近似灰度矩阵就会造成干扰。使得最后匹配的数据出现了错误，造成一段一段的碎片，给人工干预时造成了一定的麻烦。通过反面的拼接去检验正面拼接的正确性。

七．模型的评价与推广

7．1 模型的评价

（1）问题一中的连续性模型对于拼接边缘信息量较大的碎片有较高的效率以及很高的准确率，但是当单独用该模型解决例如附件三、四的小碎片时，虽然效率很高，但是准确率较低。比如，如果有两张或者多张图片边缘切割都为白色时，可能就会出现无法匹配的情况，这时就需要人工干预；向量相关模型相对于文字连续性模型，具有更高的准确度。

（2）问题二中的全局搜索模型不仅耗时多，而且由于给的信息很少，在这么多图片中匹配，会造成准确率很低的情况；向量投影分组模型，投影图片灰度向量到投影矩阵中，利用FCM聚类分析方法让打乱的横切及纵切的图片得以分类，从而分步实现了碎片的排序，简化了拼接过程，大大减少了循环匹配的次数；

（3）问题三中组合匹配模型将附件五中的a，b两图片上下拼接，然后用拼接后的图片进行分类，这样不仅提高了效率，还一定程度上增加了碎片所提供的信息。

7. 2 模型的推广

这三种模型针对不同的情况，利用多种模型和匹配方法，能够较好的解决题目中的三个问题。

但是，我们仍然可以考虑其他特征，结合连续性模型或者向量相关模型综合考虑，比如字宽特征，计算两边的碎片边缘被切开字的缺损字宽，两边相加，当和值与标准字宽相差较大时，就可以排除不利因素。

现在已经有很多模式识别的算法和软件，我们可以利用文字识别算法来计算拼接后的两片碎片上的文字上的准确率，当准确率较高时，则认为匹配成功。利用已有的技术，可以大大效率有准确率

八．参考文献

[1] 章毓晋. 图像处理（第三版）. 清华大学出版社，2012.2

[2] 边肇祺，张学工. 模式识别（第二版）.清华大学出版社 2000.1

[3] 冯宇平,戴明,孙立悦，张威. 图像自动拼接融合的优化设计.光学精密工程.2012,18（2）

[4] 李仁发，杨高波. 特征提取与图像处理（第二版）.电子工业出版社 2010.10

[5] 陈丽莉，刘贵喜.一种有效的序列图像自动拼接方法. 光电子激光. 2011,22（7）

 

 

 

 

 

 

 

九．附录

附录一：程序代码

% 第一问代码 文件名：Qusetion1.m

files=dir(‘C:\Users\ZYF\Desktop\新建文件夹\B\附件1\*.bmp’);    %批量载入图像

for n=1:numel(files)

 image{n}=imread([‘C:\Users\ZYF\Desktop\新建文件夹\B\附件1\’files(n).name]);

end

[h,z]=size(image{1,1});

for k=1:n

   byz(:,k)=image{1,k}(:,1);      %将第k张图片的最左边一列放入矩阵byz的第k列                         

   byy(:,k)=image{1,k}(:,z);      %将第k张图片的最右边一列放入矩阵byy的第k列

end

%利用页边距寻找第一张图片

for i=1:n

    sum=0;

    for j=1:h

        if byz(j,i)==255

            sum=sum+1;

        else

            break;

        end

    end

    if sum==h

        f=i;

    end

end

paixu=zeros(1,n);

index=1;

paixu(index)=f; 

 

%依据连续性模型需找匹配点

for i=2:n

    max=0;

    for j=1:n

        sumofbp=0;

        num=0;

        for k=2:h-1

            ifbyy(k,paixu(index))~=255

                ifbyz(k,j)<255||byz(k-1,j)<255||byz(k+1,j)<255

                    num=num+1;

                else

                    num=num;

                end;

            end

        end

    if num>max

       max=num;

       signal=j;

    end

  end

    index=index+1;

    paixu(index)=signal;               %存放排好序的图片序号

end

temp=image{paixu(1)};

for i=2:n

    temp=[tempimage{paixu(i)}];       %将排序好的图片存放与temp       

end

imshow(temp)                           %完整显示整张纸片

 

 

%第二问中文拼接中投影代码   文件名reflect.m

% 碎片预处理，图像投影，存放投影数组

files=dir(‘C:\Users\ZYF\Desktop\新建文件夹\B\附件3\*.bmp’);%载入图像

figure;

A=zeros(1,180);

for n=1:numel(files)

image{n}=imread([‘C:\Users\ZYF\Desktop\新建文件夹\B\附件3\’ files(n).name]);

end

[x,y]=size(image{1});

flag1=zeros(x,n);

for i=1:n

    for j=1:x

        sum=0;

        for k=1:y

            ifimage{i}(j,k)<255       

                break;

            else

                sum=sum+1;

            end

        end

        if sum==y

            flag1(j,i)=0;

        else

            flag1(j,i)=1;

        end

    end

end

 

 

 

%如果采用掩码模型，则运行代码yanma.m（包含3个函数top.m,mid.m,back.m）

%附件三掩码补充代码   文件名   yanma.m

files4=dir(‘C:\Users\asus\Desktop\2013B3\附件3\*.bmp’);%载入图像

for n4=1:numel(files4)

 image4{n4}=imread([‘C:\Users\asus\Desktop\2013B3\附件3\’ files4(n4).name]);

end

fid1=fopen(‘C:\Users\asus\Desktop\数模数据.txt’,’wt’);

fid2=fopen(‘C:\Users\asus\Desktop\需补充.txt’,’wt’);

[x,y]=size(image4{1});

flag=zeros(x,n4);

%向量投影

for i=1:n4

    for j=1:x

        sum=0;

        for k=1:y

            ifimage4{i}(j,k)<255

                break;

            else

                sum=sum+1;

            end

        end

        if sum==y

            flag(j,i)=0;

        else

            flag(j,i)=1;

        end

    end

end

 

sumofb=0;

for i=1:209

    sumofb=0;

    for j=1:179      

       ifflag(j,i)==1&&flag(j+1,i)==0             

              sumofb=sumofb+1;

       else

              sumofb=sumofb;

       end    

    end

    if flag(180,i)==1

        sumofb=sumofb+1;

    end

    numofb(i)=sumofb;

end

for i=1:209

    if numofb(i)<3

        fprintf(fid2,’%g ‘,i);

    end

end

flagnew=flag;

A=[5 9 15 17 22 26 28 33 41 61 67 71 72 75 86 90 94 102 107 109 110111 114 115 118 120 124 126 140 141 146 147 151 153 154 155 156 158 166 167 174182 185 186 188 195 197 198 205 206 208];

[ax,ay]=size(A);

shul=zeros(ay,6);

for i=1:ay%统计投影白色0和黑色1的数量

    sumofd=0;

    index=1;

    if flag(1,A(i))==1%若第一个为黑色，则白色个数为0

        shul(i,index)=0;

        index=index+1;

    end

    for j=1:179

        ifflag(j,A(i))==flag(j+1,A(i))

            sumofd=sumofd+1;

        else

            sumofd=sumofd+1;

           shul(i,index)=sumofd;

            index=index+1;

            sumofd=0;

        end

    end

    shul(i,index)=sumofd+1;

end

for i=1:ay

    if shul(i,1)>26

        topout=top(shul(i,1));

        hebin(i,:)=[topoutshul(i,2:6)];

    end

end

for i=1:ay

    for j=3

        if shul(i,j)>31

           midout=mid(shul(i,j));

           hebin(i,:)=[shul(i,1:2) midout shul(i,4:6)];

        end

    end

end

for i=1:ay

    for j=5

        if shul(i,j)>26

           backout=back(shul(i,j));

           hebin(i,:)=[shul(i,1:4) backout];

        end

    end

end

 for i=1:ay

     if hebin(i,1)~=0

        temp=hebin(i,1);

     else

         temp=1;

     end

     for j=2:2:6

        flagnew(temp:(temp+hebin(i,j)),A(i))=1;

        temp=temp+hebin(i,j)+hebin(i,j+1);

     end

 end

 

 

%top函数代码   文件名top.m

%top函数        

 function [ topout ] = top( in)

if in<69

    topout=[0 in-26 26];

elseif 68<in<95

    topout=[in-68 42 26];

elseif 94<in<137

    topout=[0 in-94 26 42 26];

elseif 136<in<163

    topout=[in-136 42 26 4226];

else

    topout=[0 in-162 26 42 2642 26];

end

end

 

%mid函数   文件名   mid.m

%mid函数

function [ midout ] = mid( in )

if in<101

    midout=[26 in-52 26];

elseif 100<in<163

    midout=[26 42 26 in-12026];

end

end

 

%back函数   文件名 back.m

%back函数

function [ backout ] = back( in )

if in<69

    backout=[26 in-26 0 0];

elseif 68<in<95

    backout=[26 42 in-68 0];

elseif 94<in<137

    backout=[26 42 26 in-94];

end

end

 

 

%第二问C均值分类代码  文件名Classify.m

%模糊C均值（fcm）分类

clear;

close all;

load flag1.mat;

files=dir(‘C:\Users\ZYF\Desktop\新建文件夹\B\附件3\*.bmp’);%载入图像

figure;

for n=1:numel(files)

 image{n}=imread([‘C:\Users\ZYF\Desktop\新建文件夹\B\附件3\’ files(n).name]);

end

data = flag1′;

[center,U,obj_fcn] = fcm(data, 11);

maxU = max(U);

%index(i)中存放第i类分组的图片

index(1).t = find(U(1,:) == maxU);

index(2).t = find(U(2, :) == maxU);

index(3).t = find(U(3,:) == maxU);

index(4).t = find(U(4,:) == maxU);

index(5).t = find(U(5,:) == maxU);

index(6).t = find(U(6,:) == maxU);

index(7).t = find(U(7,:) == maxU);

index(8).t = find(U(8,:) == maxU);

index(9).t = find(U(9,:) == maxU);

index(10).t = find(U(10,:) == maxU);

index(11).t= find(U(11,:) == maxU);

 

 

 

%第二问中文拼接代码   文件名Question_Chinese.m

clear;

close all;

% 问题二汉字匹配拼接

load index.mat;

class=12;

files=dir(‘C:\Users\ZYF\Desktop\新建文件夹\B\附件3\*.bmp’);%载入图像

 

for n=1:numel(files)

 image{n}=imread([‘C:\Users\ZYF\Desktop\新建文件夹\B\附件3\’ files(n).name]);

end

 

for k=1:n

    bz(:,k)=image{1,k}(:,1);                 %将第k张图片的最左边一列放入矩阵bz的第k列

   br(:,k)=image{1,k}(:,72);               %将第k张图片的最右边一列放入矩阵br的第k列

end

ind=1;

for oo=1:class

    tmp=[];

    first=index(oo).t;                      %将index分组的第oo组存放入first矩阵

    cd=length(first);

    f=zeros(1,cd);                         %标记图片是否已被使用，初始为0

     kk=0;

    for j=1:cd

        sum=0;

        for p=1:180

            for q=1:5

             ifimage{first(1,j)}(p,q)==255

                sum=sum+1;

             end

            end

        end

        if sum==900

            figure (oo);

            subplot(1,cd,1)

            imshow( image{first(j)});

            kk=first(j);

           f(1,1)=first(j);                 %已用图片

            break;

        end

    end

    jj=1;

    if(kk==0)

       figure (oo);

            subplot(1,cd,1)

            imshow( image{first(1)});

            kk=first(1);

           f(1,1)=first(1);                % 已用图片

    end

    tmp=[tmp kk];

    sign=kk;

    for z=1:cd

        max=0;

        for a=1:cd

           sum1=0;

           hh=0;

          for ll=1:cd

             if(first(a)==f(1,ll))

                  hh=1;

              end

          end

          if(hh==0)

             co=corrcoef(double(bz(:,first(a))),double(br(:,kk)));% 相关性函数判断

                 sum1=abs(co(1,2));

           if(max<sum1)

               max=sum1;

               sign=first(a);

           end

          end

        end

 

    if(kk ~= sign)

        tmp=[tmp sign];

        subplot(1,cd,jj+1)

        imshow(image{sign});

        kk=sign;                          %现在图片

        f(1,jj+1)=sign;

        jj=jj+1;

    else

       for d=1:cd

             for s=1:cd

                 gg=0;

                if(first(d) ==f(1,s))

                  gg=1;

                 end

             end

              if(gg==0)

                  kk=first(d);

                  break;

              end

        end

        cc(ind).a=tmp;

        ind=ind+1;

        tmp=[kk];

     end

    end

 end

 

 

%第二问英文添加直线代码  文件名  Line.m

% 英文直线的修补

clear;

close all;

files=dir(‘.\附件4\*.bmp’);%载入图像

for n=1:numel(files)

   image{n}=imread([‘.\附件4\’ files(n).name]);

   A(n).t=sum(image{n},2);

end

 

B=[12,20,15,25,12,20,15,25];%做模板

B1=[12,20,15,25,12,20,15,25,12,20,15,25];

B2=[20,15,25,12,20,15,25,12,20,15,25,12];

B3=[15,25,12,20,15,25,12,20,15,25,12,20];

B4=[25,12,20,15,25,12,20,15,25,12,20,15];

idx1=zeros(600,1);% 模板数组

idx1(1,1)=1;

mm=1;

for i=1:6

   for j=1:4

       mm=mm+B(j);

       idx1(mm,1)=1;

   end

end

 

%ind=A(10).t;

BZ=zeros(180,209);

for pp=1:209

   ind=A(pp).t;

   for i=2:179   % 拐点找出

       if(ind(i-1)-ind(i)>10 &&ind(i+1)-ind(i)>10)

           BZ(i,pp)=1;

       end

   end

   if ind(1)<ind(2)

       BZ(1,pp)=1;

   end

   if ind(180)<ind(179)

       BZ(180,pp)=1;

   end

   po=find(BZ(:,pp)==1);

   gg=1;

   max=0;

    for ii=1:5  % 与模板匹配

       dd=0;

       fh=0;

       for z=po(1):180

           if(BZ(z,pp)==1&&idx1(z+gg,1)==1||z+1<=180&&BZ(z+1,pp)==1&&idx1(z+gg,1)==1||(z-1)~=0&& BZ(z-1,pp)==1&&idx1(z+gg,1)==1)% 与模板匹配

                dd=dd+1;

           end

        end

       if(max<dd)

           SG=ii;

           max=dd;

           kh=po(1);

       end

       gg=gg+B(ii);

   end

   

   if SG==1||SG==4

       AB=kh;

       j=1;

       while AB-B1(5-j)>=1

           BZ(AB-B1(5-j))=1;

           AB=AB-B1(5-j);

           j=mod(j+1,4);

       end

       AD=kh;

       j=1;

       while AD+B1(j)<=180

           BZ(AD+B1(j),pp)=1;

           AD=AD+B1(j);

           j=j+1;

       end

   end

   if SG==2       

       AB=kh;

       j=1;

        while AB-B2(5-j)>=1

           BZ(AB-B2(5-j))=1;

           AB=AB-B2(5-j);

           j=mod(j+1,4);

       end

       AD=kh;

       j=1;

       while AD+B2(j)<=180

           BZ(AD+B2(j),pp)=1;

           AD=AD+B2(j);

           j=j+1;

       end

   end

   if SG==3

       AB=kh;

       j=1;

       while AB-B3(5-j)>=1

           BZ(AB-B3(5-j))=1;

           AB=AB-B3(5-j);

           j=mod(j+1,4);

       end

       AD=kh;

       j=1;

       while AD+B3(j)<=180

           BZ(AD+B3(j),pp)=1;

           AD=AD+B3(j);

           j=j+1;

       end

   end

   if SG == 4

       AB=kh;

       j=1;

       while AB-B4(5-j)>=1

           BZ(AB-B4(5-j))=1;

           AB=AB-B4(5-j);

           j=mod(j+1,4);

       end

       AD=kh;

        j=1;

       while AD+B4(j)<=180

           BZ(AD+B4(j),pp)=1;

           AD=AD+B4(j);

           j=j+1;

       end

   end

end

 

%第二问英文拼接主代码  文件名  Question.m

clear;

close all;

load index2.mat;

class=12;

files=dir(‘C:\Users\ZYF\Desktop\新建文件夹\B\附件4\*.bmp’);%载入图像

for n=1:numel(files)

   image{n}=imread([‘C:\Users\ZYF\Desktop\新建文件夹\B\附件4\’files(n).name]);

end

for k=1:n

   bz(:,k)=image{1,k}(:,1); %首行

   br(:,k)=image{1,k}(:,72);%末行

end

ind=1; % 类别计数器

for oo=1:class

   dx=0;   %  倒序寻找

   tmp=[];

   first=index2(oo).t;

   cd=length(first);

   f=zeros(1,length(first));  %标记

   kk=0;

   while (sum(f)<length(first))

       if length(tmp)==0            % 找行首块

           for j=1:length(first)

                if f(j)==0

                    im=image{ first(j)};

                    sumim=sum(im,1);

                    ifsum(sumim(1:10))==255*180*10  % 找到行首

                        figure (oo);

                       subplot(1,length(first),1)

                        imshow( image{first(j)});

                        kk=first(j);

                        f(j)=1;% 标记已用图片

                        break;

                    end

                end

           end

           % 找块尾

           for j=1:length(first)

                if f(j)==0

                    im=image{ first(j)};

                    sumim=sum(im,1);

                    ifsum(sumim(70:72))==255*180*3  % 找到行尾

                        figure (oo);

                       subplot(1,length(first),1)

                        imshow( image{ first(j)});

                        kk=first(j);

                        f(j)=1;% 标记已用图片

                        dx=1;

                        break;

                    end

                end

           end           

           if(kk==0)  % dou找不到，用第可用一个图片

                figure (oo);

                subplot(1,length(first),1);

                imshow( image{ first(1)});

                pos=find(f==0);

                kk=first(pos(1));

                f(pos(1))=1; % 标记已用图片

           end

           tmp=[tmp kk];

       end       

       maxsum=0; % 找最接近的

       sign=kk;

       for z=1:length(first)

           if f(z)==0   % 没有用过

                sum1=0;

                for p=1:180

                    if dx==1

                        cha=abs(bz(p,kk)-br(p,first(z)));

                        if ( cha ==0 &&bz(p,kk)~= 255 && br(p,first(z))~=255)

                            sum1=sum1+1;

                        end

                    else

                       cha=abs(br(p,kk)-bz(p,first(z)));

                       if ( cha <20&& br(p,kk)~= 255 && bz(p,first(z))~=255)

                            sum1=sum1+1;

                        end

                    end

                end

                if(maxsum<sum1)

                    maxsum=sum1;

                   fpos=z;

                    sign=first(z);

                end

           end

       end

       if maxsum<1

           sign=kk;

       end

       if(kk~=sign)

           %找到了

           if dx==1

                tmp=[sign tmp ];

           else

                tmp=[tmp sign];

           end

           imshow(image{sign});

           kk=sign;%现在图片

           f(fpos)=1;

       else            %没找到

           cc(ind).a=tmp;ind=ind+1;

           kk=0;tmp=[];dx=0;

       end

   end

end

for i=1:length(cc)

   figure(20);clf;

   for j=1:length(cc(i).a)

       subplot(1,length(cc(i).a),j);

       imshow(image{cc(i).a(j)});

   end

   pause;

end

 

%第三问英文拼接主代码   文件名  Question3_English.m

clc,clear;

% 碎片匹配连接

for n=1:209

   fnamea=[num2str(n-1,’%03d’) ‘a.bmp’];

   fnameb=[num2str(n-1,’%03d’) ‘b.bmp’];

   image5{n}.a=imread([‘.\附件5\’ fnamea]);

   image5{n}.b=imread([‘.\附件5\’ fnameb]);

   image5a{2*n-1}=[image5{n}.a;fliplr(image5{n}.b)];%碎片a、b组合连接

   image5a{2*n} =[image5{n}.b;fliplr(image5{n}.a)];  

end

figure(1);clf;

subplot(2,1,1);imshow(image5{1}.a);

subplot(2,1,2);imshow(image5{1}.b);

figure(2);clf;

subplot(1,2,1);imshow(image5a{1});title(‘ab’);% 显示组合效果

subplot(1,2,2);imshow(image5a{2});title(‘ba’);

save image5.mat;

%load image5

n=209;

for k=1:2*n

   bz(:,k)=image5a{1,k}(:,1);

   br(:,k)=image5a{1,k}(:,72);

end

first=zeros(1,22);

last=zeros(1,22);

flag=zeros(2*n,1);

for i=1:2*n

   im=image5a{i};

   sim=sum(im,1);

   if sum(sim(1:5))==360*255*5

       flag(i)=1;  % 标记行首

    end

   if sum(sim(72-4:72))==360*255*5

       flag(i)=2; % 标记行尾

   end

end

first=find(flag==1);

last=find(flag==2);

ind=1;

flg=zeros(2*n,1); % 判断是否被用过

for hh=1:length(first)

   tmp=[];

   k=first(hh);

   tmp=[tmp k];

   flg(k)=1;

   ry=1;% 另起一行的标志

   while ry == 1

       maxsum=0;

       for i=1:2*n

           sum1=0;

           if( (flag(i)~= 1) && (flg(i)==0) )

                co=corrcoef(double(bz(:,i)),double(br(:,k)));

                 sum1=abs(co(1,2));

                if(maxsum<sum1)

                    maxsum=sum1;

                    sign=i;

                end

           end

       end

       if(k ~= sign) % 找到了

           tmp=[tmp sign]

           k=sign; % 现在图片

           flg(k)=1;

           ry=1;

       else

           cc(ind).a=tmp; % 没找到

           ind=ind+1;

           ry=0;

       end

   end

end

save cc.mat cc

% for i=1:length(cc)

%    figure(i);clf;

%    for j=1:length(cc(i).a)       

%        leibie(i,j)=cc(i).a(j);

%        subplot(1,length(cc(i).a),j);

%        imshow(image5a{cc(i).a(j)});

%    end

% end

 

%第三问英文拼接图片显示代码   文件名  Question3show.m

% 附件5碎片拼接后，每一行的显示

load image5.mat;

load cc.mat;

close all;

for i=1:length(cc)

   figure(i);clf;

   for j=1:length(cc(i).a)       

       leibie(i,j)=cc(i).a(j);

       subplot(1,length(cc(i).a),j);

       imshow(image5a{cc(i).a(j)});

   end

end

附件二：实验结果

    附件1结果：

 

附件2结果：

  

附件3结果：

 

附件4结果：

 

附件5结果：

正面：

 

 反面：

今天的文章碎纸片的拼接复原分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。