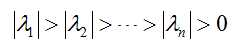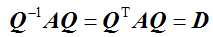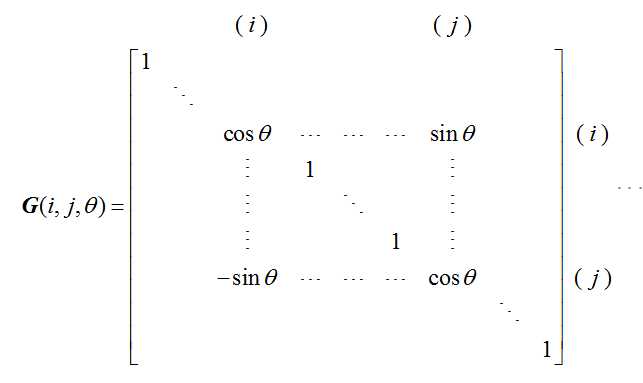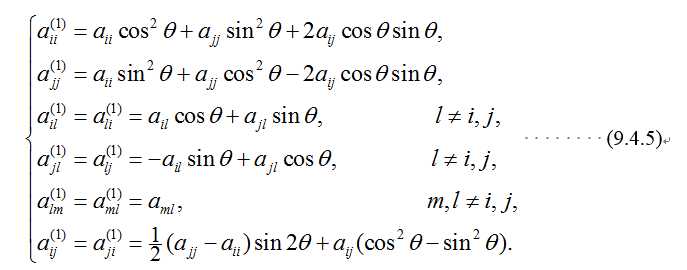最近项目中有一个模块需要求矩阵的最大特征值和特征值对应的特征向量，无奈，又重新将以前学习的这方面的知识重新温习了一遍，感觉还是当时学的不够深，所以谢谢感悟，顺便对知识点进行一个总结。
首先特征值和特征向量的求解根据项目的需求或者是矩阵的具体形式，主要可以分成如下三种形式：
- 自己只需要获得矩阵的最大特征值和特征值所对应的特征向量
- 需要求取矩阵的所有特征值
- 需要求取特征值和特征向量的矩阵为实对称矩阵，则可以通过另一种方法进行求解
现在我们来分析这三种形式特征值和特征向量的求取：
1.如果自己仅仅要求最大特征值的话肯定采用形式1的算法，该算法的优点是时间复杂度较低，计算量相对较小，该方法不但能够求取特征值和特征向量，而且只要特征值不全为0，该方法都能获得想要的结果。
2.如果需要获得一个矩阵的所有特征值，则通过形式2可以很好的解决该问题，但是该方法的缺点是仅仅能够获得特征值，获得特征值之后利用其它方法进行求解，这样做自然而然计算量就大了起来。
3.如果矩阵为实对称矩阵，那么可以通过形式3对其进行特征值和特征向量的求取，该方法相对于形式2的好处就是能够一次性将特征值和特征向量求取出来，缺点就是矩阵必须是实对称矩阵，至于算法复杂度方面我没有进行测试，不过猜测一下应该形式3复杂度相对来说要低一点（不然这种算法毫无有点怎么可能存活下来）。
下面对上面三种形式采用的算法进行说明：
乘幂法
乘幂法主要针对求取矩阵的最大特征值和特征向量，原理就是迭代求极限，推导过程如下：
首先我们不妨假设矩阵A的n个特征值的关系如下：
（1）
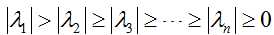
且矩阵有相应的n个线性无关的特征向量x1,x2,x3…..xn，如果学过矩阵论就会知道，上述n个线性无关特征向量构成了n为线性空间的一组基，通俗的讲就是任意一个n维的一个向量都可以用上面n个向量进行表示，例如n维向量z0表示形式如下：
（2）
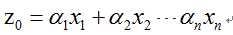
在矩阵两边同时乘以矩阵A,则有：
（3）
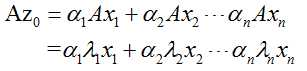
当矩阵两边连乘n个矩阵A，则有：
（4）
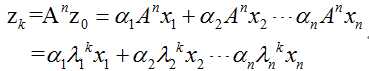
将上式进行变换后可得：
（5）
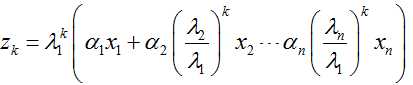
由假设可知，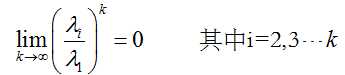
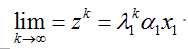
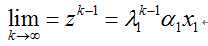
，所以可以得到：
（6）
（7）
由式（6）（7）联立可得矩阵最大特征值，结果如下：
（8）
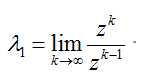
已知特征值由式（7）可得相应的特征向量：
（9）
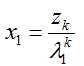
由乘幂法的迭代过程容易看出，如果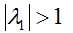
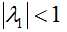
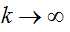
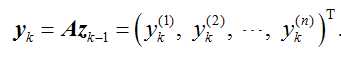
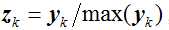
或
，那么迭代向量zk的各个非零的分量将随着
而趋于无穷（或趋于零），这样在计算机上实现时就可能上溢(或下溢). 为了克服这个缺点，需将每步迭代向量进行规范化，过程如下：
（10）
（11）
定理
设A是n阶实矩阵，取初始向量z0，通常取z0={1,1,…..,1}，其迭代过程是：对k=1,2……，有:
(12)
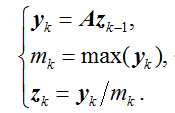
通过迭代，有：
（13）
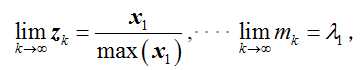
证明过程如下：
（14）
（15）
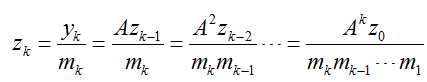
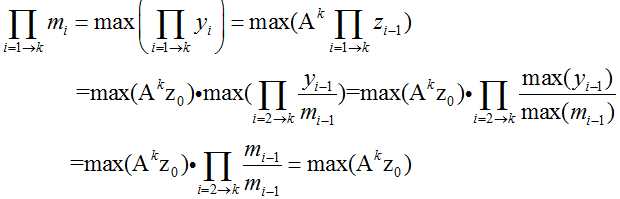
由式（14）和（15）联立可得：
（16）
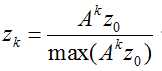
由式（4）可知：
（17）
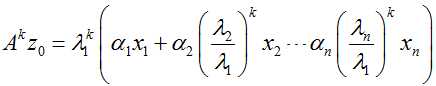
则有：
（18）
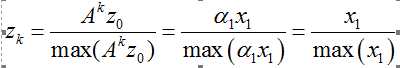
定理第一个式子得证，下面证明第二个式子：
（19）
（20）
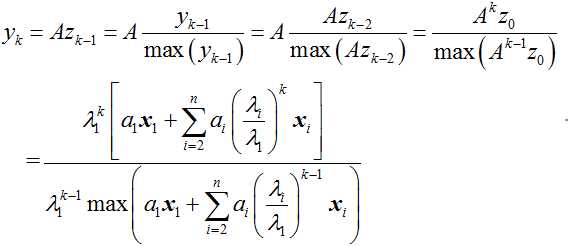
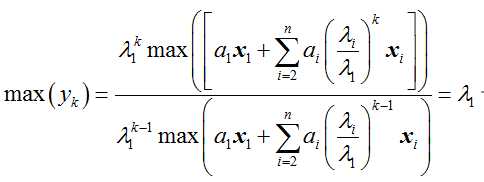
由此定理得证。
由定理可知乘幂算法步骤如下：
（1）首先寻找任意向量z0,一般情况去z0={1,1,…..1}。
（2）由z0计算得到y1,而后寻找y1向量中的最大值m1。
（3）由y1和m1得到z1,判断迭代次数是否达到，如果达到则跳到步骤4，然否则跳到步骤2循环。
（4）此时获得的mk即矩阵A的特征值，zk即为相应的特征向量，算法结束。
注：这里迭代结束判断可以是迭代次数，也可以是特征值mi前后两次的误差，我写程序的时候采用的是误差判断。
至于具体的程序，目前还未整理好，注释啥的都没写，所以暂时先不放上，等把注释写好了再贴上来。
QR算法
QR算法是针对解决形式2的算法，要看懂该算法需要一点矩阵论里面的知识，我尽量讲的通俗一点，如果还看不懂请翻翻矩阵论第四章矩阵分解的知识点。
1.QR分解
任意一个矩阵A可以分解成如下两个矩阵表达的形式：
（21）
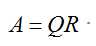
其中矩阵Q为正交矩阵，矩阵R为上三角矩阵，至于QR分解到底是怎么回事，矩阵Q和矩阵R是怎么得到的，你们还是看矩阵论吧，如果我把这些都介绍了，感觉这篇文章要写崩，或者你可以先认可我是正确的，然后往下看。
首先我们有A1=A=QR，则令A2=RQ,则有：
（22）
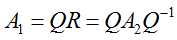
由式（22）可知，A1和A2相似，相似矩阵具有相同的特征值，说明A1和A2的特征值相同，我们就可以通过求取A2的特征值来间接求取A1的特征值。
定理
设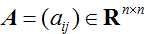
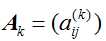
, {Ak}是由QR算法产生的矩阵序列，其中
,若满足如下条件：
（1）矩阵A的特征值满足
（2）
，其中
，而且P有三角分解P=LU，(L是单位下三角矩阵，U是上三角矩阵)。
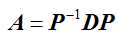
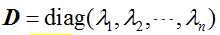
则有：
（23）
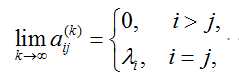
上面的定理我就不证明了，因为我也不会，本人矩阵论学的也是二把刀，请见谅，但是看到上面的定理的两个条件是否能引起你的注意，首先是条件1，该条件严重限制了该方法的使用范围，矩阵的特征值不能相同且不能为0，条件2表明矩阵A能够对角化。
其大概原理就是如此，下面我们来说明QR算法的具体步骤：
（1）首先矩阵Ai进行QR分解，根据得到矩阵Qi和Ri
（2）根据矩阵Qi和Ri，得到Ai+1=Ri*Qi
（3）判断是否跳出循环条件，如果跳出循环条件则跳到步骤4，否则跳到步骤1进行循环
（4）由得到的矩阵Ai+1，该矩阵对角线上元素为矩阵A的特征向量。
Jacobi方法
Jacobi方法主要针对实对称矩阵，首先要对实对称矩阵的性质进行说明，实对称矩阵的特征向量都为正交向量，并且存在如下关系：
上式中Q为正交矩阵，由此可见，Jacobi方法的实质和关键就是找一个正交矩阵Q，将矩阵A化为对角矩阵。
矩阵中存在两种线性变换，Givens变换和Householder变换，两种变换的共同点就是变换矩阵为正交阵。由此我们可以通过Givens变换或者Householder变换将矩阵A化为对角阵，而相应的变换矩阵的列向量即为特征向量，变换后的对角阵元素即为特征值。下面来介绍一波Givens变换：
Givens变换
设矩阵A是n阶实对称矩阵，称n阶矩阵,存在矩阵G
上面矩阵G为Givens变换对应的变换矩阵（其本质是将向量逆时针旋转一定角度后的新向量），通过改变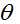
左乘该矩阵可以将第i行第j列的元素变成0，通过(n-1)(n-2)/2次变换即可将n*n矩阵变换成对角阵，这就是Jacobi方法的原理。
注：左乘矩阵G只会改变原来矩阵第i行，第i列；第j行；第j列中的元素，所以通过下面式子可以很快利用原矩阵获得新矩阵的各个元素，计算式子如下：
不知道你们对上面的说的算法原理之后会不会产生一个疑问，如果我经过一次变换将一个元素变成0之后下一次变换后会不会该元素会不会又不为0了？？答案是肯定会的，但是为啥这样的算法还能用呢？？下面定理解决了这个疑问：
上述定理可知，Givens变换后矩阵各个元素的总和是不变的，而可以证明，我们每次变换之后，非对角线上的元素的总和都变小了，相应的对角线上的元素都变大了，所以当非对角线上元素总和小于某个误差值时，我们可以认为对角线上的元素即为特征值，这就是上述定理的理论依据。
Jacobi算法步骤：
（1）找到矩阵Ai中非对角线上最大的元素，将利用Givens变换将该元素变换成0
（2）利用公式可以得到变换后的矩阵Ai+1。
（3）获得左乘矩阵Gi。
（4）计算变换后矩阵Ai+1的非对角线元素和，如果满足小于误差值的要求即跳到步骤5，否则跳到步骤1进行循环
（5）变换后矩阵Ak对角线元素即为特征值，变换矩阵Gk*Gk-1……..G1连乘得到矩阵G,G的列向量即为特征向量。
至于代码，整理好再贴出来。
今天的文章矩阵特征值和特征向量的求取分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请发送邮件至 举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/28711.html
