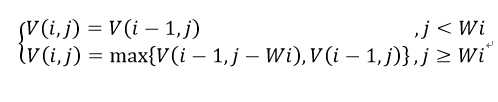1. 编程号首页

背包问题（01背包问题，多重背包问题，完全背包问题）——基于python的动态规划

编程小号 • • 未分类

背包问题（01背包问题，多重背包问题，完全背包问题）——基于python的动态规划1.0-1背包问题1.1题目描述有一个包和n个物品，包的容量为m，每个物品都有各自的体积和价值，问当从这n个物品中选择多个物品放在包里而物品体积总数不超过包的容量m时，能够得到的最大价值是多少？[对于每个物品不可以取多次，最多只能取一次，之所以叫做0-1背包，0表示不取，1表示取]1.2思路动态规划，根据动态规划解题步骤（建立模型、寻找约束条件、找子问题之间的的递推关系式、填表（区间模…

1. 0-1背包问题

1.1 题目描述

有一个包和n个物品，包的容量为m，每个物品都有各自的体积和价值，问当从这n个物品中选择多个物品放在包里而物品体积总数不超过包的容量m时，能够得到的最大价值是多少？[对于每个物品不可以取多次，最多只能取一次，之所以叫做0-1背包，0表示不取，1表示取]

1.2思路

动态规划，根据动态规划解题步骤（建立模型、寻找约束条件、找子问题之间的的递推关系式、填表（区间模型）、得到解）找出0-1背包问题的最优解以及解组成。

1.3 步骤

首先定义：Vi表示标号为i物品的价值，Wi表示标号为i物品的体积。capacity为背包的最大容量。那么一个0-1背包问题的具体步骤如下：

  1. 建立模型，我们要求在物品总体积限制为capacity的情况下，尽可能装下价值高的物品组合，其模型如下：
    在这里插入图片描述
  2. 寻找状态转换方程，即子问题之间的递推关系，我们令V(i,j)表示当前背包为容量 j，前 i 个物品最佳组合对应的价值最优解，那么就有两种可能：
    a）包的容量比该商品体积小，即j < Vi，装不下第i个物品。此时背包容量为j，前i个物品的最优解与背包容量为j，前i-1个物品最佳组合对应的最优解是一样的，即V(i,j)=V(i-1,j)
    b）当包的容量等于或大于该商品的体积，即j >= Vi，能装下第i个物品。那无非有两种情况，在前i个物品，背包容量为j的最优组合里有第i个物品，但同时占据了背包Wj个容量，V(i,j) = V(i-1,j-Wi)+Vi；在前i个物品，背包容量为j的最优组合里没有第i个物品，此时V(i,j) = V(i-1,j)。所以，根据最优性原理，背包容量为j，前i个物品的最优解V(i,j) 要取这两种情况的最大值，V(i,j) = max{V(i-1,j),V(i-1,j-Wi)+Vi},
由此可以得出递推关系式：

在这里插入图片描述
3. 根据递推公式进行逐行填表，初始化表V(i,o) = 0，V(0,j) = 0,表的列维度从0到n，行维度从0到capacity。
4. 根据填表过程，编写代码。

1.3 举例

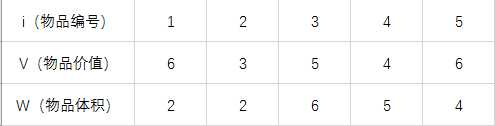
有如下几种物品，物品的价值和体积如表所示：
在这里插入图片描述
首先定义：Vi表示标号为i物品的价值，Wi表示标号为i物品的体积。另外背包的总体积为10。

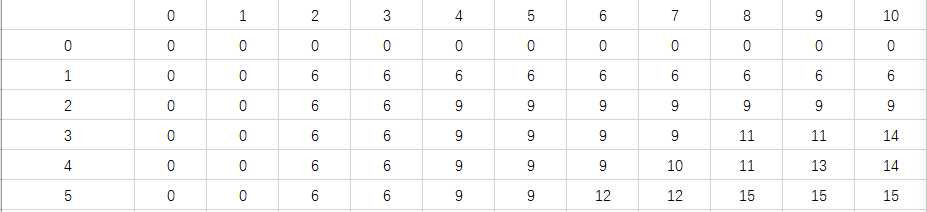
1.3.1 填表

填表过程如下：
在这里插入图片描述

1.4 python实现

def  zeroOneBag(num,capacity,weightList,valueList):
    valueExcel= [[0 for j in range(capacity + 1)] for i in range(num + 1)]
    for i in range(1,num+1):
        for j in range(1,capacity+1):
            valueExcel[i][j] = valueExcel[i - 1][j]
            if j >= weightList[i-1] and valueExcel[i][j] < (valueExcel[i - 1][j - weightList[i - 1]] + valueList[i - 1]):
                valueExcel[i][j] = (valueExcel[i - 1][j - weightList[i - 1]] + valueList[i - 1])
    return valueExcel
print(zeroOneBag(5,10,[2,2,6,5,4],[6,3,5,4,6]))
# 输出结果为：
[[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], 
[0, 0, 6, 6, 6, 6, 6, 6, 6, 6, 6], 
[0, 0, 6, 6, 9, 9, 9, 9, 9, 9, 9], 
[0, 0, 6, 6, 9, 9, 9, 9, 11, 11, 14],
[0, 0, 6, 6, 9, 9, 9, 10, 11, 13, 14], 
[0, 0, 6, 6, 9, 9, 12, 12, 15, 15, 15]]

因此该问题的价值最大组合为15。

1.4.1 算法优化

上面这种写法的时间复杂度为o（nc），空间复杂度也为o（nc）。时间复杂度不能在优化了，但是空间复杂度可以进行优化，使之降低到o（c）。

def zeroOneBagOpt(num,capacity,weightList,valueList):
    valueRes = [0 for i in range(capacity+1)]
    for i in range(1, num + 1):
        for j in range(capacity, 0, -1):
            if j >= weightList[i-1]:
                valueRes[j] = max(valueRes[j-weightList[i-1]]+valueList[i-1], valueRes[j])
        # i变一次，数组的更新一次，利用数组的不断更新，达到上面的方法动态规划的目的。
        # 当j遍历更新完一遍valueRes，valueRes就相当于完成上边方法中表第i+1行的填充.
        # 必须从后向前遍历和判断储存结果的数组，因为valueRes[j-weightList[i-1]]+valueList[i-1]就相当于V(i-1,j-Wi)+ Vi
        # 判断第i个物品是否是最优解的时候，需要以i-1的情况为基础，不能掺杂有关第i个物品的信息，
        # 如果从前往后遍历，那么valueRes[:j]的数是判断了i之后的，会产生错误。
        # 这里的value[j]即为上一次最佳结果，从后向前可以在遍历到j的未知的时候，不破坏j前面的上一次的最佳结果。
        # 
    return valueRes
print(zeroOneBagOpt(5,10,[2,2,6,5,4],[6,3,5,4,6]))
# 输出结果为：[0, 0, 6, 6, 9, 9, 12, 12, 15, 15, 15]

1.4.2 找到最佳组合的构成

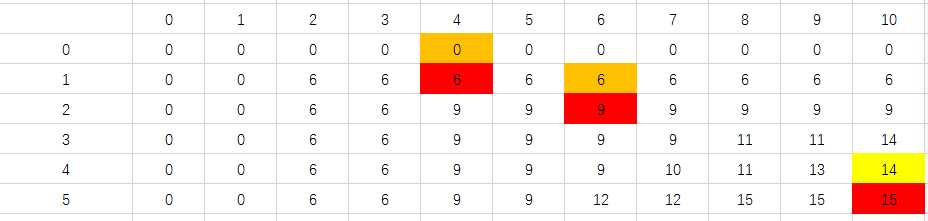
通过上面的方法可以求出背包问题的最优解，但还不知道这个最优解由哪些商品组成，故要根据最优解回溯找出解的组成，根据填表的原理可以有如下的寻解方式：

  1. V(i,j)=V(i-1,j)时，说明没有选择第i 个商品，则回到V(i-1,j)；
  2. V(i,j)!=V(i-1,j)时，说明装了第i个商品，该商品是最优解组成的一部分，一定有V(i,j)=V(i-1,j-w(i))+v(i)，随后我们得回到装该商品之前，即回到V(i-1,j-w(i))；
  3. 重复1,2，一直遍历到i＝0结束为止，所有解的组成都会找到。
    在这里插入图片描述
    最优解的组成由第1个，第2个，第5个。
def showRes(num,capacity,weightList,valueExcel):
    indexRes = []
    j = capacity
    for i in range(num,0,-1):
        if valueExcel[i][j] != valueExcel[i-1][j]:
            indexRes.append(i)
            j -= weightList[i-1]
    return indexRes
valueExcel = (zeroOneBag(5,10,[2,2,6,5,4],[6,3,5,4,6]))
print(showRes(5,10,[2,2,6,5,4],valueExcel))
# 输出结果为：[5, 2, 1]

2. 多重背包问题

2.1 问题详解

在这里插入图片描述

2.2 题目思路

2.2.1 一般思路

在这里插入图片描述
例如，第i种物品有3个，因此可以把这三个物品进行拆分，看作是不同种类的物体，不过是具有相同体积和价值的不同物品，通过拆分，就把可以放多个同种物品拆分成只能放0个或者一个“不同”物品的0-1背包问题。

2.2.1 python代码

# weightList：每种物品的体积
# valueList：每种物品的价值
# numList：每种物品的数量
def trans(weightList,valueList,numList):      # 转换函数 
    K = len(numList)
    newWeightList = []
    newValueList = []
    num = sum(numList)
    for i in range(K):
        for j in range(numList[i]):
            newWeightList.append(weightList[i])
            newValueList.append(valueList[i])
    return num,newValueList,newWeightList
def zeroOneBag(numList,capacity,weightList,valueList):
 	# 先将多重问题转成0-1问题，利用0-1问题的代码。
    num,newValueList,newWeightList = trans(weightList,valueList,numList)
    valueExcel= [[0 for j in range(capacity + 1)] for i in range(num + 1)]
    for i in range(1,num+1):
        for j in range(1,capacity+1):
            valueExcel[i][j] = valueExcel[i - 1][j]
            if j >= newWeightList[i-1] and valueExcel[i][j] < (valueExcel[i - 1][j - newWeightList[i - 1]] + newValueList[i - 1]):
                valueExcel[i][j] = (valueExcel[i - 1][j - newWeightList[i - 1]] + newValueList[i - 1])
    return valueExcel
print(zeroOneBag([2,5,10],8,[2,2,1],[20,10,6]))
# 输出结果：
#[[0, 0, 0, 0, 0, 0, 0, 0, 0],
# [0, 0, 20, 20, 20, 20, 20, 20, 20], 
# [0, 0, 20, 20, 40, 40, 40, 40, 40],
# [0, 0, 20, 20, 40, 40, 50, 50, 50],
# [0, 0, 20, 20, 40, 40, 50, 50, 60],
# [0, 0, 20, 20, 40, 40, 50, 50, 60],
# [0, 0, 20, 20, 40, 40, 50, 50, 60],
# [0, 0, 20, 20, 40, 40, 50, 50, 60],
# [0, 6, 20, 26, 40, 46, 50, 56, 60],
# [0, 6, 20, 26, 40, 46, 52, 56, 62],
# [0, 6, 20, 26, 40, 46, 52, 58, 62],
# [0, 6, 20, 26, 40, 46, 52, 58, 64],
# [0, 6, 20, 26, 40, 46, 52, 58, 64],
# [0, 6, 20, 26, 40, 46, 52, 58, 64],
# [0, 6, 20, 26, 40, 46, 52, 58, 64],
# [0, 6, 20, 26, 40, 46, 52, 58, 64],
# [0, 6, 20, 26, 40, 46, 52, 58, 64],
# [0, 6, 20, 26, 40, 46, 52, 58, 64]]

最终的最大价值为64。和0-1背包问题一样，可以对空间进行优化，这里就省略了。

2.2.2 优化

利用一般的思路讲多重背包问题转化成0-1背包问题进行解决，某种物品有多少个就要拆分成多少个不同的物品，这会增加时间复杂度和空间复杂度。因此我们可以利用另一种分解方法：二进制分解
在这里插入图片描述

二进制分解代码
def binaryDecomposition(n):  # 二进制分解
     k = 0
     res = []
     while n - 2**(k+1) + 1  > 0:
         res.append(2**k)
         k += 1
     res.append(n-2 ** (k) + 1)
     return res

如果第i种物品有13个，根据这种思路，13拆分成1,2，4,6。只需要将这种物品拆分成4个物品，这四个物品的体积和价值分别是（Wi,Vi），（2Wi,2Vi），（4Wi,4Vi），（6Wi,6Vi），而不是13个物品，这就降低了时间复杂度和空间复杂度。

2.2.2 python代码

# optimization
def binaryDecomposition(n):  # 二进制分解
     k = 0
     res = []
     while n - 2**(k+1) + 1  > 0:
         res.append(2**k)
         k += 1
     res.append(n-2 ** (k) + 1)
     return res
def trans(weightList,valueList,numList):
    newWeightList = []
    newValueList = []
    for i in range(len(numList)):
        for j in binaryDecomposition(numList[i]):
            newWeightList.append(j * weightList[i])
            newValueList.append(j * valueList[i])
    num = len(newValueList)
    return num,newValueList,newWeightList
def  zeroOneBag(numList,capacity,weightList,valueList):
    num,newValueList,newWeightList = trans(weightList,valueList,numList)
    valueExcel= [[0 for j in range(capacity + 1)] for i in range(num + 1)]
    for i in range(1,num+1):
        for j in range(1,capacity+1):
            valueExcel[i][j] = valueExcel[i - 1][j]
            if j >= newWeightList[i-1] and valueExcel[i][j] < (valueExcel[i - 1][j - newWeightList[i - 1]] + newValueList[i - 1]):
                valueExcel[i][j] = (valueExcel[i - 1][j - newWeightList[i - 1]] + newValueList[i - 1])
    return valueExcel
print(zeroOneBag([2,5,10],8,[2,2,1],[20,10,6]))
# 输出结果为：
[[0, 0, 0, 0, 0, 0, 0, 0, 0],
#[0, 0, 20, 20, 20, 20, 20, 20, 20],
#[0, 0, 20, 20, 40, 40, 40, 40, 40],
#[0, 0, 20, 20, 40, 40, 50, 50, 50],
#[0, 0, 20, 20, 40, 40, 50, 50, 60],
#[0, 0, 20, 20, 40, 40, 50, 50, 60],
#[0, 6, 20, 26, 40, 46, 50, 56, 60],
#[0, 6, 20, 26, 40, 46, 52, 58, 62],
#[0, 6, 20, 26, 40, 46, 52, 58, 64],
#[0, 6, 20, 26, 40, 46, 52, 58, 64]]

通过输出结果也可以看出，表的维度比上一种方法要低。最终的最佳组合的价值为64。

3.完全背包问题

3.1 问题描述

在这里插入图片描述

3.2.1 思路

完全背包问题和多重背包问题以及0-1背包问题的唯一不同就在于在背包容量允许的情况下，可以在背包里放无限个同一种物品。
下面是0-1背包问题的递推公式：
在这里插入图片描述
我们仍然令V(i,j)表示当前背包为容量 j，前 i 个物品最佳组合对应的价值最优解。那么我们可以根据这个0-1背包问题的状态转换方程通过变化，得到完全背包问题的递推公式。
在这里插入图片描述

3.2 python代码

def compKnap(num,capacity,weightList,valueList):
    valueExcel = [[0 for j in range(capacity + 1)] for i in range(num + 1)]
    for i in range(1, num + 1):
        for j in range(1, capacity + 1):
            for k in range((j // weightList[i - 1]) + 1):
                if valueExcel[i][j] < (valueExcel[i - 1][j - k*weightList[i - 1]] + k*valueList[i - 1]):
                    valueExcel[i][j] = (valueExcel[i - 1][j - k * weightList[i - 1]] + k*valueList[i - 1])
    return valueExcel
# print(compKnap(5,16,[5,4,7,2,6],[12,3,10,3,6]))
""" 输出结果为： [[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 12, 12, 12, 12, 12, 24, 24, 24, 24, 24, 36, 36], [0, 0, 0, 0, 3, 12, 12, 12, 12, 15, 24, 24, 24, 24, 27, 36, 36], [0, 0, 0, 0, 3, 12, 12, 12, 12, 15, 24, 24, 24, 24, 27, 36, 36], [0, 0, 3, 3, 6, 12, 12, 15, 15, 18, 24, 24, 27, 27, 30, 36, 36], [0, 0, 3, 3, 6, 12, 12, 15, 15, 18, 24, 24, 27, 27, 30, 36, 36]] """

3.2.2 优化

和0-1背包问题一样，完全背包问题也可以通过二进制分解来进行拆分，来降低时间复杂度和空间复杂度。同时，还可以优化，将其优化成和相同条件下0-1背包问题时间复杂度、空间复杂度一样的算法。
其方法和0-1背包问题的优化方法一样。都是借助一个一维数组。

3.2.2 python 代码

def compKnapOpt(num,capacity,weightList,valueList):
    valueExcel = [0 for j in range(capacity + 1)]
    for i in range(1, num + 1):
        for j in range(1, capacity + 1):
            if weightList[i-1]<=j:
                valueExcel[j] = max(valueExcel[j - weightList[i - 1]] + valueList[i - 1], valueExcel[j])
    return valueExcel
print(compKnapOpt(5,16,[5,4,7,2,6],[12,3,10,3,6]))
# 输出结果：
[0, 0, 3, 3, 6, 12, 12, 15, 15, 18, 24, 24, 27, 27, 30, 36, 36]

在这里插入图片描述

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请发送邮件至 举报，一经查实，本站将立刻删除。
如需转载请保留出处：http://bianchenghao.cn/28980.html

赞 (0)
编程小号编程小号
0

相关推荐

发表回复

您的电子邮箱地址不会被公开。 必填项已用*标注