向量旋转公式

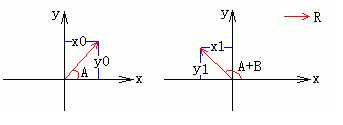
在二维坐标系中，一个位置向量的旋转公式可以由三角函数的几何意义推出。

比如上图所示是位置向量R逆时针旋转角度B前后的情况。

      在左图中，我们有关系：

　　x0 = |R| * cosA       =>          cosA = x0 / |R|

　　y0 = |R| * sinA        =>          sinA = y0 / |R|

  　在右图中，我们有关系：

　　x1 = |R| * cos（A+B）

　　y1 = |R| * sin（A+B）

　　其中（x1， y1）就是（x0， y0）旋转角B后得到的点，也就是位置向量R最后指向的点。我们展开cos（A+B）和sin（A+B），得到：

　　x1 = |R| * （cosAcosB – sinAsinB）

　　y1 = |R| * （sinAcosB + cosAsinB）

　　现在把  cosA = x0 / |R| 和 sinA = y0 / |R|  代入上面的式子，得到：

x1 = |R| *（x0 * cosB / |R| – y0 * sinB / |R|）=>  x1 = x0 * cosB – y0 * sinB

y1 = |R| *（y0 * cosB / |R| + x0 * sinB / |R|）=>y1 = x0 * sinB + y0 * cosB

　　这样我们就得到了二维坐标下向量围绕圆点的逆时针旋转公式。顺时针旋转就把角度变为负：

　　x1 = x0 * cos（-B） – y0 * sin（-B） =>  x1 = x0 * cosB + y0 * sinB

　　y1 = x0 * sin（-B） + y0 * cos（-B）=>  y1 = -x0 * sinB + y0 * cosB

　　现在我要把这个旋转公式写成矩阵的形式，有一个概念我简单提一下，平面或空间里的每个线性变换（这里就是旋转变换）都对应一个矩阵，叫做变换矩阵。对一个点实施线性变换就是通过乘上该线性变换的矩阵完成的。好了，打住，不然就跑题了。

所以二维旋转变换矩阵就是：

                   [cosA  sinA]          [cosA –sinA]                                          

           [-sinA cosA] 或者  [sinA cosA]

我们对向量进行旋转变换可以通过矩阵完成，比如我要向量（x， y）绕原点逆时针旋转角度A：

 [x, y] x  [cosA  sinA] = [x*cosA-y*sinA  x*sinA+y*cosA]

                                  [-sinA cosA]

      旋转后的向量为：[x*cosA-y*sinA  x*sinA+y*cosA]

今天的文章向量旋转公式分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。