极限中0除以常数_基本不等式中常用公式百度作业帮

1. 基本不等式中常用公式

基本不等式中常用公式：

(1)√((a²+b²)/2)≥(a+b)/2≥√ab≥2/(1/a+1/b)。(当且仅当a=b时，等号成立)

(2)√(ab)≤(a+b)/2。(当且仅当a=b时，等号成立)

(3)a²+b²≥2ab。(当且仅当a=b时，等号成立)

(4)ab≤(a+b)²/4。(当且仅当a=b时，等号成立)

(5)||a|-|b| |≤|a+b|≤|a|+|b|。(当且仅当a=b时，等号成立)

扩展资料：

不等式的特殊性质有以下三种：

①不等式性质1：不等式的两边同时加上(或减去)同一个数(或式子)，不等号的方向不变；

②不等式性质2：不等式的两边同时乘(或除以)同一个正数，不等号的方向不变；

③不等式性质3：不等式的两边同时乘(或除以)同一个负数，不等号的方向变。总结：当两个正数的积为定值时，它们的和有最小值；当两个正数的和为定值时，它们的积有最大值。

参考资料：百度百科-基本不等式

基本不等式的变形公式一共有几个

5个

基本不等式通常是指均值不等式,常见的有变形有以下几种

a>=0,b>=0

a+b>=2根号(ab)

a²+b²>=2ab

2(a²+b²)>=(a+b)²

(1/a)+(1/b)>=4/(a+b)

扩展资料：

基本不等式是主要应用于求某些函数的最值及证明的不等式。其表述为：两个正实数的算术平均数大于或等于它们的几何平均数。

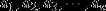
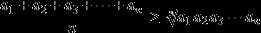
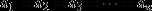
一般地，若是正实数，则有均值不等式当且仅当取等号

和积互化和定积最大

当

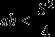
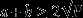
一定时，，且当时取等号积定和最小当一定时，，且当时取等号

参考资料：百度百科-基本不等式

基本不等式公式大全

1. √(ab)≤(a+b)/2

2. a^2-2ab+b^2 ≥ 0

3. a^2+b^2 ≥ 2ab

不等式公式，是两头不对等的公式，是一种数学用语。

绝对值不等式公式：| |a|-|b| |≤|a-b|≤|a|+|b|和| |a|-|b| |≤|a+b|≤|a|+|b|。

常用的不等式的基本性质：

1. a>b,b>c→a>c;

2. a>b →a+c>b+c;

3. a>b,c>0 → ac>bc;

4. a>b,c<0→ac<bc;

5. a>b>0,c>d>0 → ac>bd;

6. a>b,ab>0 → 1/a<1/b;

7. a>b>0 → a^n>b^n;

高中常用的不等式公式有哪些？

高中常用的不等式公式有：

(1)(a+b)/2≥√ab

(2)a^2+b^2≥2ab

(3)(a+b+c)/3≥(abc)^(1/3)

(4)a^3+b^3+c^3≥3abc

(5)(a1+a2+…+an)/n≥(a1a2…an)^(1/n)

(6)2/(1/a+1/b)≤√ab≤(a+b)/2≤√[(a^2+b^2)/2]

扩展资料：

不等式基本性质：

①如果x>y，那么y<x；如果y<x，那么x>y；(对称性)

②如果x>y，y>z；那么x>z；(传递性)

③如果x>y，而z为任意实数或整式，那么x+z>y+z；(加法原则，或叫同向不等式可加性)

④ 如果x>y，z>0，那么xz>yz；如果x>y，z<0，那么xz<yz；(乘法原则)

⑤如果x>y，m>n，那么x+m>y+n；(充分不必要条件)

不等式两边相加或相减同一个数或式子，不等号的方向不变。(移项要变号)

不等式两边相乘或相除同一个正数，不等号的方向不变。(相当系数化1，这是得正数才能使用)

不等式两边乘或除以同一个负数，不等号的方向改变。(÷或×1个负数的时候要变号)

参考资料：百度百科—基本不等式

基本不等式公式是什么

基本不等式公式：a+b≥2√(ab)。a大于0，b大于0，当且仅当a=b时，等号成立。

常用不等式公式：

①√((a²+b²)/2)≥(a+b)/2≥√ab≥2/(1/a+1/b)

②√(ab)≤(a+b)/2

③a²+b²≥2ab

④ab≤(a+b)²/4

⑤||a|-|b| |≤|a+b|≤|a|+|b|

扩展资料：

基本不等式应用：

1、应用基本不等式解题一定要注意应用的前提：“一正”“二定”“三相等”。所谓“一正”是指正数,“二定”是指应用基本不等式求最值时,和或积为定值,“三相等”是指满足等号成立的条件．

2、在利用基本不等式求最值时,要根据式子的特征灵活变形,配凑出积、和为常数的形式,然后再利用基本不等式。

3、条件最值的求解通常有两种方法：

(1)一是消元法,即根据条件建立两个量之间的函数关系,然后代入代数式转化为函数的最值求解；

(2)二是将条件灵活变形,利用常数“1”代换的方法构造和或积为常数的式子,然后利用基本不等式求解最值。