大白话说float型的精度和范围

考研复习C++看到书上写float的范围为-3.4×10³⁸ ~ 3.4×10³⁸，有效数字为7位，不太明白，看了几篇大佬的博客后略知一二。
自己尝试把一些晦涩的词汇用浅显的话再解释一遍，总结的可能不是很专业全面，希望对同样入门的小伙伴有所帮助。

关于float的结构

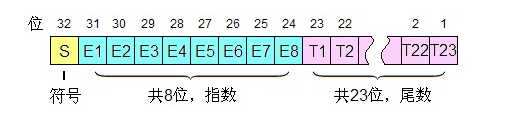
float型数据共占4个字节即32位
其中1位符号位，8位指数部分，23位尾数部分

在内存中按逆字节存储（即顺序与上图相反）

float表示数据的原理

先看科学计数法
对于十进制数10.25 科学计数法为1.025×10¹
换算为二进制为1010.01 科学计数法为1.01001×2³

可以看出任意一个实型数可用二进制科学计数法表示为a×2^b
其有效数字的范围a∈[1,2),即1.xxxx的形式，
整数部分1我们不管，把小数点后边的部分xxxx存储起来就是尾数部分m（23位）

而指数部分2^b 的幂b就存储为指数部分e （8位）
这样数据的表示方法就是（1+m)×2^e

float型的范围和精度

说清楚表示原理再解释范围和精度就比较方便了
由上述可得尾数部分m的范围为0.000…0.000~0.111…111，十进制为[0,1-2^-23],再加上前面不管的整数部分1，有效数字的范围为[1,2-2^-23]

那么就可以解释精度了。由于尾数部分位数是固定的小数点后23位，23位所能表示的最大数是2^23−1=8388607，所以float最多能表示小于1/8388607的精度，即7位有效数字。

再看指数部分e，8位指数部分[0,255],其中0和255分别用来表示0和无穷大，1~254用来表示规范数字，可以表示的范围为[-126，127]，所以科学计数法的后半部分范围为[2^-126,2¹²⁷]

综上把有效数字和指数合起来看便能得到（1+m)×2^e 的
绝对值最小值1.0×2^-126≈1.175×10³⁸
绝对值最大值(2-2^-23)*2¹²⁷≈3.4×10³⁸

参考博客
准确详解：C/C++ float、double数据类型的表示范围及精度.
c++ float类型研究.
有补充及不足希望在评论区指出，谢谢

今天的文章大白话说float型的精度和范围分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。