摘要：

        采用BP神经网络拟合目标函数，并添加高斯随机噪声，通过使用feedforwardnet函数构建BP神经网络进行函数拟合。通过调试设定的参数及所使用的训练函数，得出结论：BP神经网络可以较好地解决黑盒问题。且随着设定参数的提升及采用的训练函数的改变，会对BP神经网络的拟合效果造成较大的影响，因此要想得到较好的拟合效果，需要设定合适的训练参数及采用对应情况下的训练函数。

1.1 BP神经网络原理

        BP神经网络是一种按误差反向传播(简称误差反传)训练的多层前馈网络，其算法称为BP算法，它的基本思想是梯度下降法，利用梯度搜索技术，以期使网络的实际输出值和期望输出值的误差均方差为最小。

        基本BP算法包括信号的前向传播和误差的反向传播两个过程：即计算误差输出时按从输入到输出的方向进行，而调整权值和阈值则从输出到输入的方向进行。正向传播时，输入信号通过隐含层作用于输出节点，经过非线性变换，产生输出信号，若实际输出与期望输出不相符，则转入误差的反向传播过程。误差反传是将输出误差通过隐含层向输入层逐层反传，并将误差分摊给各层所有单元，以从各层获得的误差信号作为调整各单元权值的依据。通过调整输入节点与隐层节点的联接强度和隐层节点与输出节点的联接强度以及阈值，使误差沿梯度方向下降，经过反复学习训练，确定与最小误差相对应的网络参数(权值和阈值)，训练即告停止。此时经过训练的神经网络即能对类似样本的输入信息，自行处理输出误差最小的经过非线形转换的信息。

1.2 实验步骤

        步骤一：从目标函数 y=sin(x)*ln(x)上随机取样 2000 个点，其中 x 值的范围为[0,20]。加入最大值为 0.1 的高斯随机噪声；

        步骤二：利用 feedforwardnet 函数构建 4 层神经网络（1 层输入层， 2 层隐藏层分别包含 30/15 个神经元， 1 层输出层）；

        步骤三：将隐藏层的激活函数设置为 tansig，训练算法采用 trainlm，目标误差为 0.001，学习率为 0.01，最大迭代次数为 2000；

        步骤四：训练网络，得到预测值，将预测值和实际值绘制到一张二维图上，输出拟合准确率。

源代码如下：

%% 采用feedforwardnet构建BP神经网络进行函数拟合
%% 清理参数及原始变量
clear al1;
close all;
clc;
%% 生成数据集，从目标函数上采样2000个点
x=rand(1,2000)*20;
x=sort(x);
y=sin(x).*log(x)+0.1.*randn(1,2000);

%% 神经网络拟合目标函数
net=feedforwardnet([20,10],'trainrp');
net.trainparam.show=50;
net.trainparam.epochs=2000;
net.trainparam.goal=1e-3;
net.trainParam.lr=0.01;
net=train(net,x,y);
view(net)
y1=net(x);

%% 统计拟合正确率（95%置信区间）
n=length(y1);
hitNum=0;
for i=1:n
    if(abs((y(1,i)-y1(1,i))/y(1,i))<=0.05) 
        hitNum=hitNum+1; 
    end
end
sprintf('正确识别率是 %3.2f%%',100*hitNum/n)

%% 绘制对比图
plot(x,y,'r*');
hold on;
plot(x, y1,'g-','linewidth',1.5);
title(['训练函数：trainrp' '       ' '训练精度：0.001' '       ' '第1层隐藏层神经元个数：20' '       ' '第2层隐藏层神经元个数：10' '       ' '拟合正确率：' num2str(100*hitNum/n) '%']);

1.3 实验结果

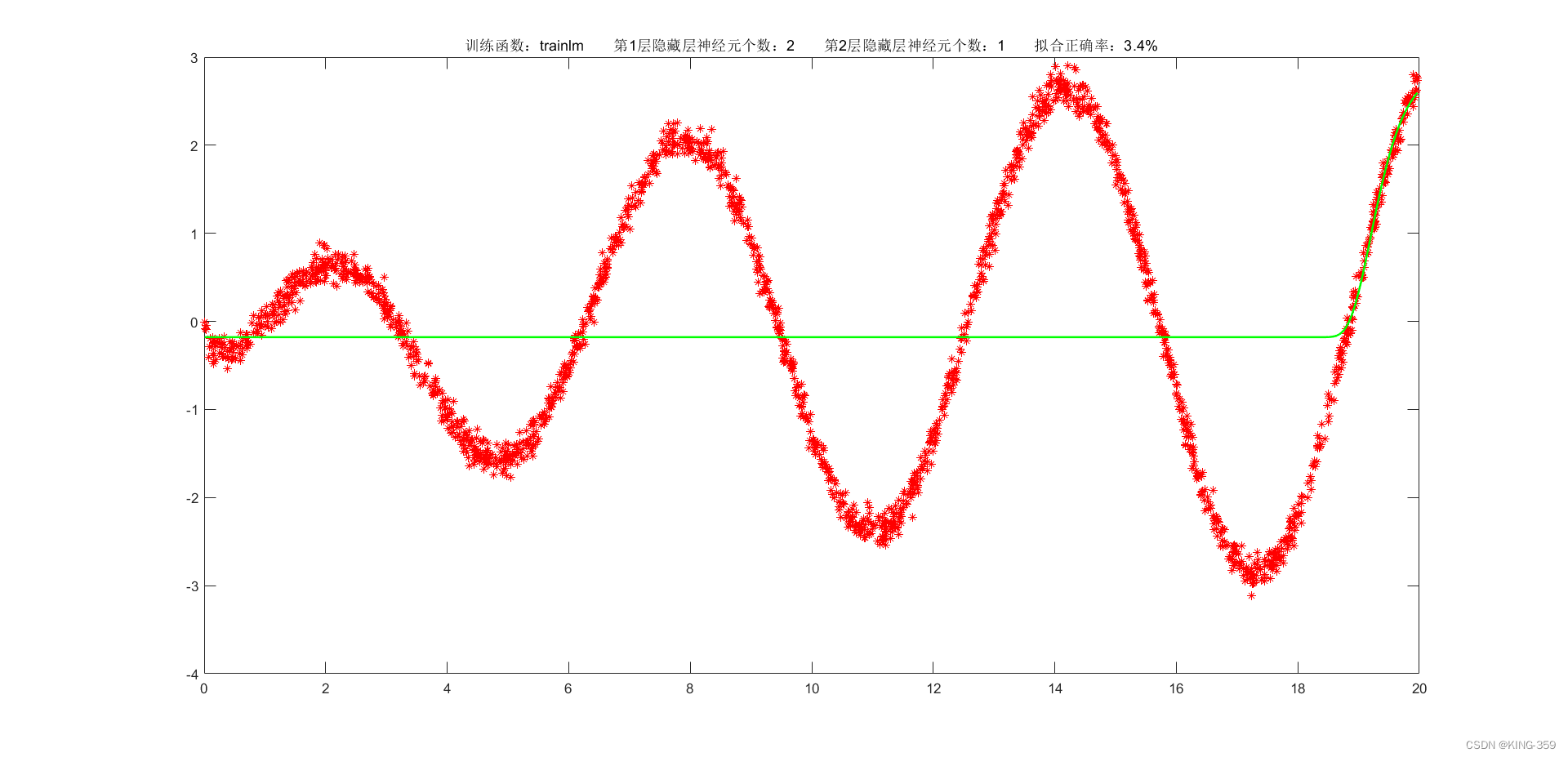
        隐藏层激活函数设置为 tansig，2层隐藏层分别包含2/1个神经元，训练算法采用 trainlm，目标误差为 0.001，学习率为 0.01，最大迭代次数为 2000时，实验结果如下图所示：

图1.1

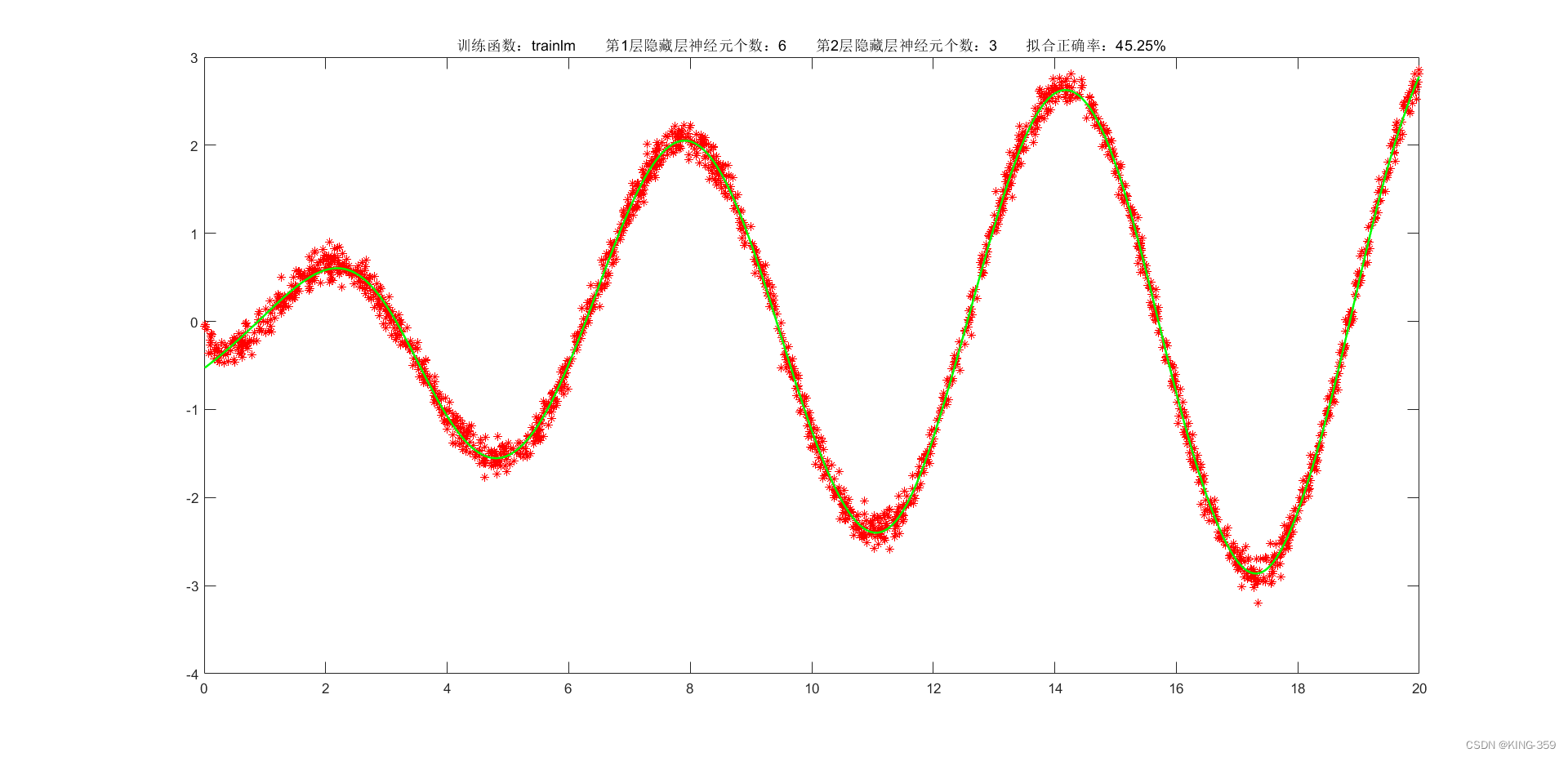
        隐藏层激活函数设置为 tansig，2层隐藏层分别包含6/3个神经元，训练算法采用 trainlm，目标误差为 0.001，学习率为 0.01，最大迭代次数为 2000时，实验结果如下图所示：

图1.2    

        隐藏层激活函数设置为 tansig，2层隐藏层分别包含10/5个神经元，训练算法采用 trainlm，目标误差为 0.001，学习率为 0.01，最大迭代次数为 2000时，实验结果如下图所示：

图1.3

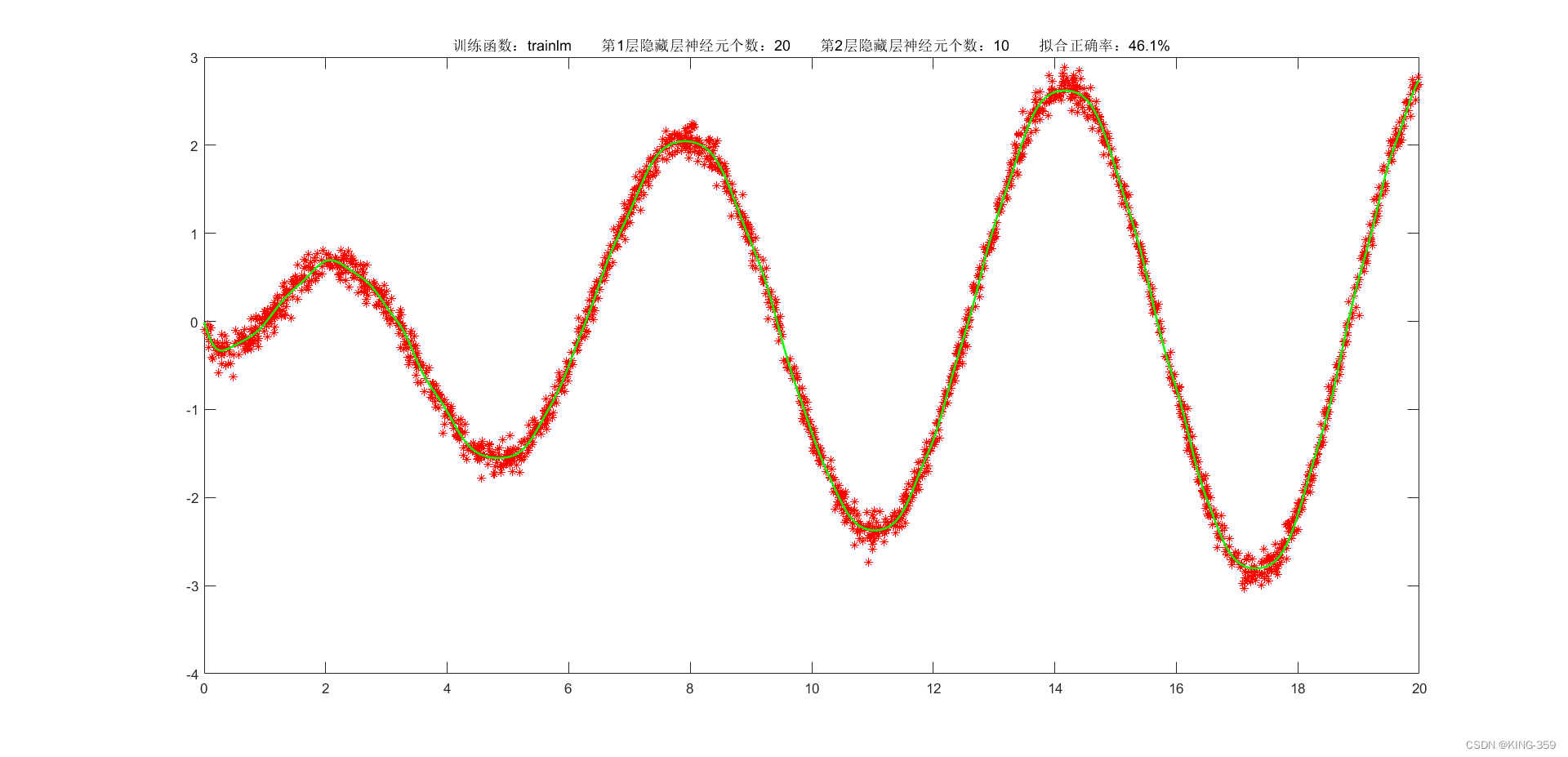
        隐藏层激活函数设置为 tansig，2层隐藏层分别包含20/10个神经元，训练算法采用 trainlm，目标误差为 0.001，学习率为 0.01，最大迭代次数为 2000时，实验结果如下图所示：

图1.4

        隐藏层激活函数设置为 tansig，2层隐藏层分别包含20/10个神经元，训练算法采用 trainlm，目标误差为 0.1，学习率为 0.01，最大迭代次数为 2000时，实验结果如下图所示：

图1.5

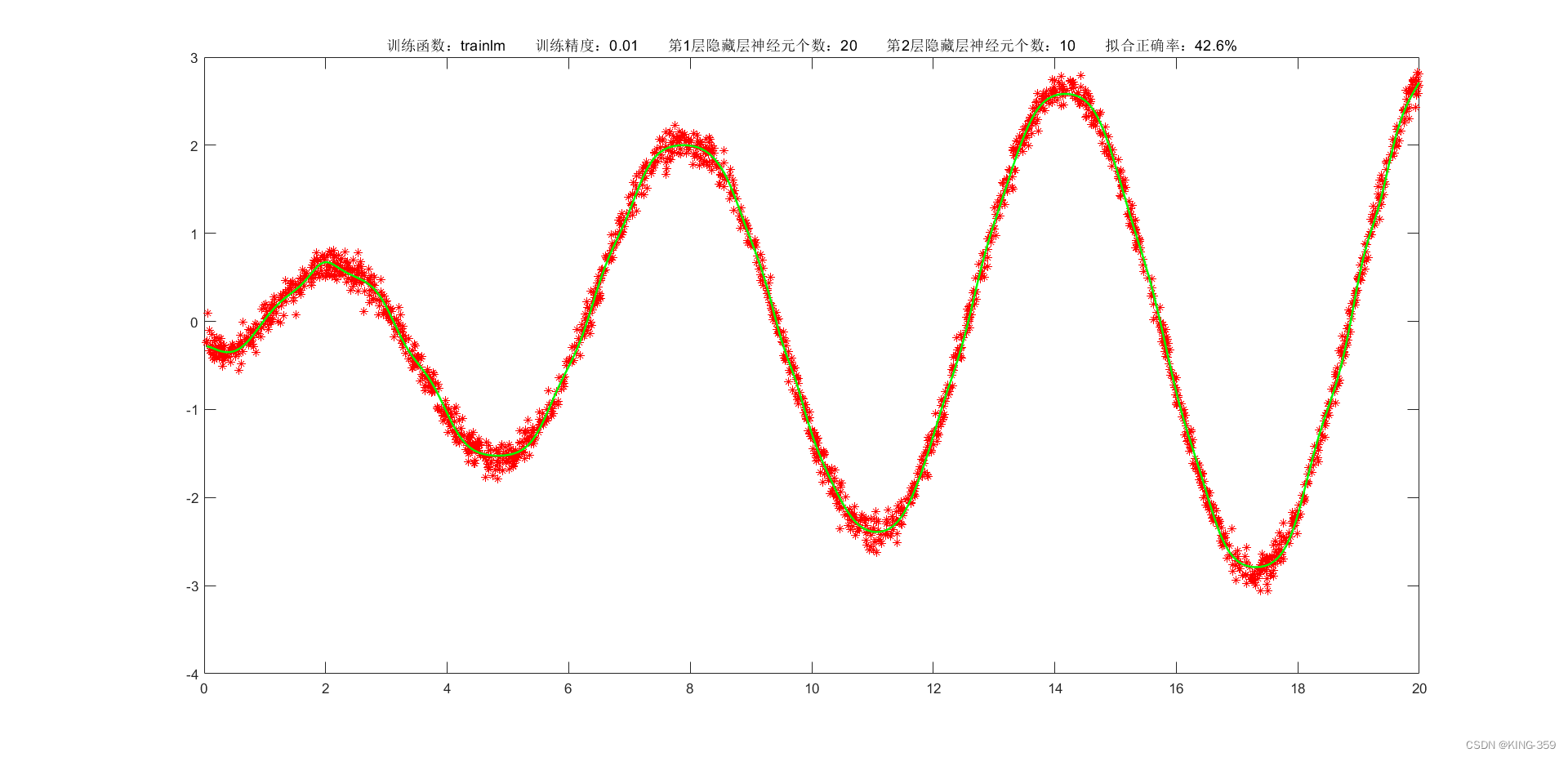
        隐藏层激活函数设置为 tansig，2层隐藏层分别包含20/10个神经元，训练算法采用 trainlm，目标误差为 0.01，学习率为 0.01，最大迭代次数为 2000时，实验结果如下图所示：

图1.6      

        隐藏层激活函数设置为 tansig，2层隐藏层分别包含20/10个神经元，训练算法采用 trainlm，目标误差为 0.001，学习率为 0.01，最大迭代次数为 2000时，实验结果如下图所示：

图1.7

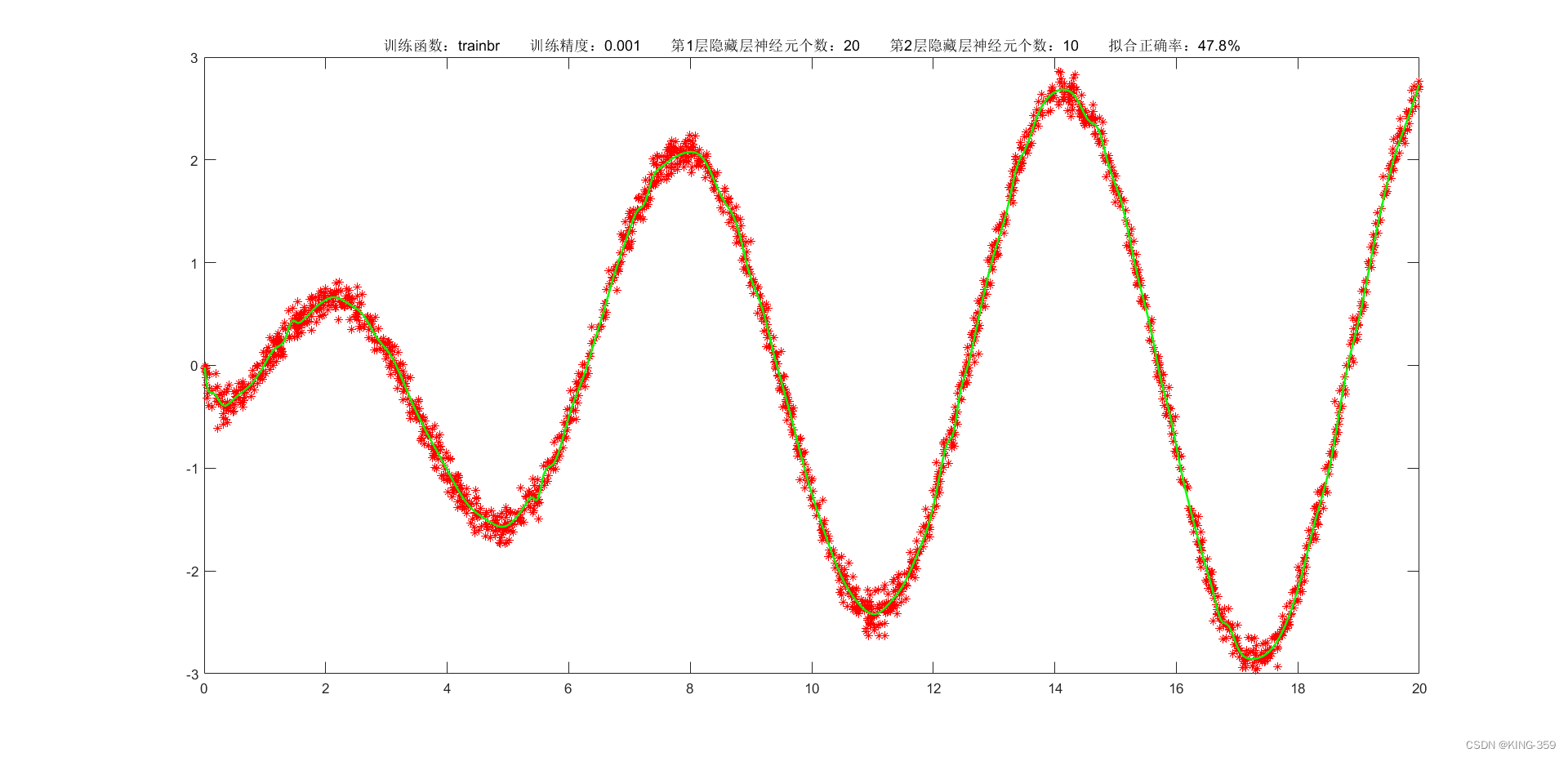
        隐藏层激活函数设置为 tansig，2层隐藏层分别包含20/10个神经元，训练算法采用 trainbr，目标误差为 0.001，学习率为 0.01，最大迭代次数为 2000时，实验结果如下图所示：

图1.8

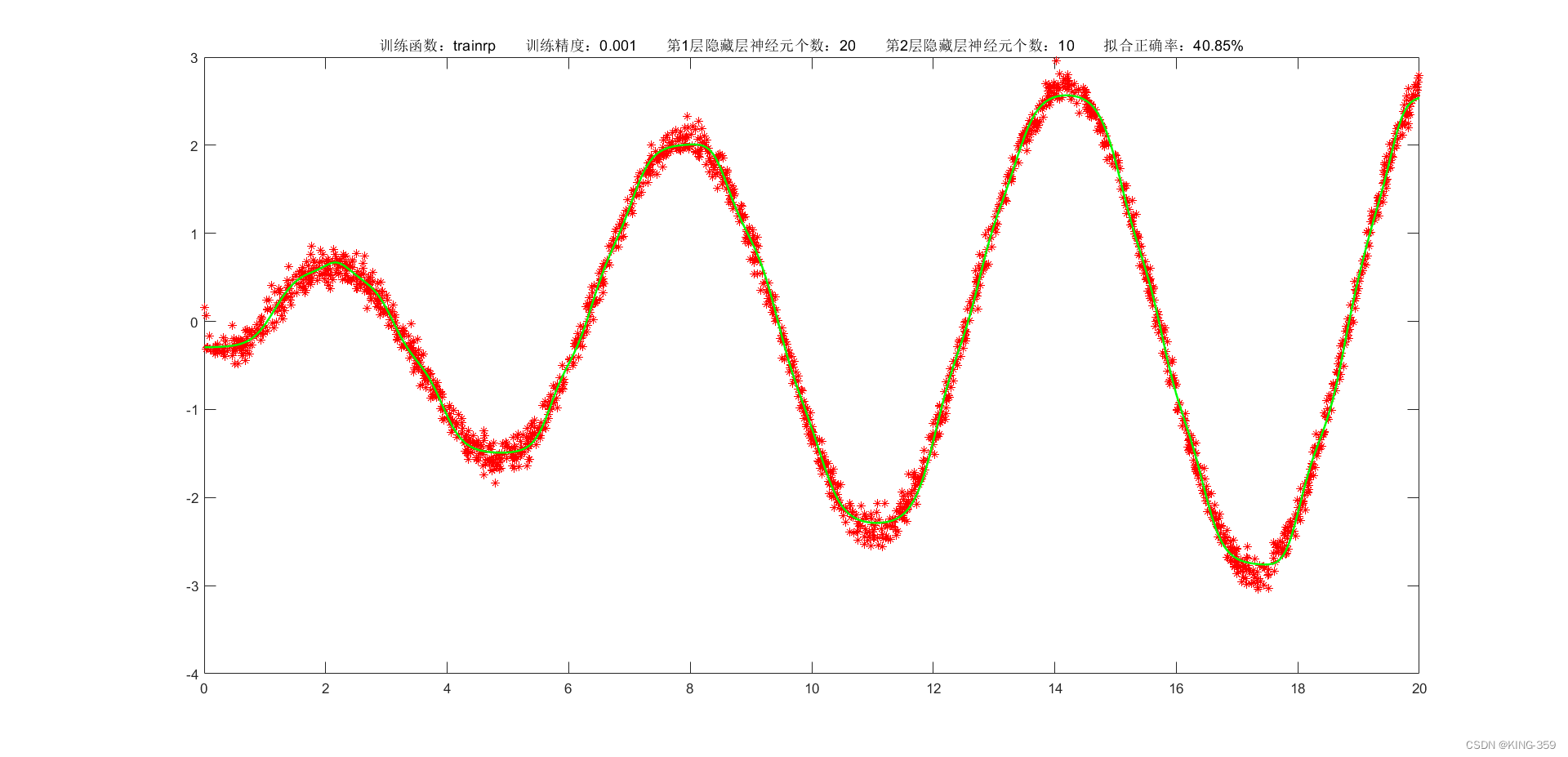
        隐藏层激活函数设置为 tansig，2层隐藏层分别包含20/10个神经元，训练算法采用 trainrp，目标误差为 0.001，学习率为 0.01，最大迭代次数为 2000时，实验结果如下图所示：

图1.9

1.4 不同参数下的结果与分析

表1

        从表1中不同参数下得到的结果可以看出：

        针对复合函数的拟合，采用feedforwardnet函数构建BP神经网络可以得到较好的拟合曲线，由于添加高斯随机噪声，所以拟合正确率不能达到很高，但是拟合出来的曲线可以较好地反映出目标函数的变化趋势。

        同时，观察不同参数下得到的结果可以发现，随着隐藏层神经元数量的增加，BP神经网络拟合曲线的效果也越来越好，但是当神经元达到一定的数量时，拟合效果会达到一个瓶颈，不能再有显著提升；随着训练精度的不断提高，BP神经网络拟合曲线的效果也越来越好；不同的训练函数有各自的的特点：

        （1）trainlm函数是Levenberg-Marquardt算法，对于中等规模的BP神经网络有最快的收敛速度，是系统默认的算法。由于其避免了直接计算赫赛矩阵，从而减少了训练中的计算量，但需要较大内存量；

        （2）trainbr函数是在Levenberg-Marquardt算法的基础上进行修改，以使网络的泛化能力更好，同时降低了确定最优网络结构的难度；

        （3）trainrp函数是有弹回的BP算法，用于消除梯度模值对网络训练带来的影响，提高训练的速度（主要通过delt_inc和delt_dec来实现权值的改变。

        由于BP神经网络能够较为方便的解决黑盒问题，它被广泛用于解决各种问题。神经网络的效果及收敛取决于所采用数据集、设定的参数及采用的训练函数。