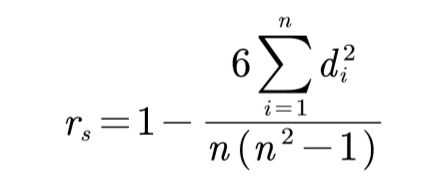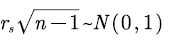spearman相关系数 matlab,数学建模——相关系数（4）——斯皮尔曼相关系数（spearman）…

文章目录

引述

一、斯皮尔曼相关系数(spearman)

1.定义1

2.定义2

3.使用MATLAB计算spearman相关系数

4. 斯皮尔曼相关系数的假设检验

二、斯皮尔曼相关系数与皮尔逊相关系数的比较

引述

经过之前几节的学习，我们了解并掌握了皮尔逊相关系数。在学习中我们发现，皮尔逊相关系数的使用条件相当苛刻：两组变量必须是连续数据、呈现正态分布，且两者间必须成线性关系。如果我们在数学建模中拿到一组数据无法满足以上条件，那么有没有其他的方法去判断两组变量之间的相关性呢？答案是肯定的，它就是斯皮尔曼相关系数(spearman).

一、斯皮尔曼相关系数(spearman)

1.定义1

定义：X和Y为两组数据，其斯皮尔曼(等级)相关系数：

其中，di为Xi和Yi之间的等级差。可以证明：rs位于-1和1之间。

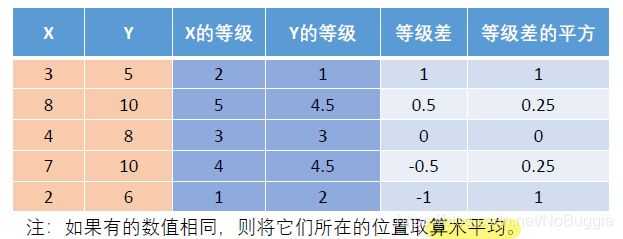
等级差

一个数的等级，就是将它所在的一列按照从小到大排序后，这个数所在的位置。

根据公式计算可得：

X和Y的斯皮尔曼相关系数 rs = 0.875

2.定义2

另一种斯皮尔曼相关系数被定义成等级之间的皮尔逊相关系数。值得注意的是，MATLAB使用的是该定义下的计算方式。

对于上图，使用MATLAB求解皮尔逊相关系数

%% 使用MATLAB求解皮尔逊相关系数

RX = [2 5 3 4 1]

RY = [1 4.5 3 4.5 2]

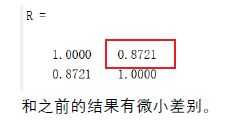
R = corrcoef(RX,RY)

计算结果如下：

3.使用MATLAB计算spearman相关系数

1. 两种用法

用法1：

corr(X, Y, ‘type’, ‘Spearman’) % X和Y必须是列向量！

用法2：

corr(X, ‘type’, ‘Spearman’) % 这时计算X矩阵各列之间的斯皮尔曼相关系数

2. 使用MATLAB计算斯皮尔曼相关系数

注：我们所使用的测试数据即为上图。

%% 斯皮尔曼相关系数

X = [3 8 4 7 2]’ % 一定要变成列向量，” ‘ “表示求转置。X = [3 8 4 7 2] 此时为行向量，转置后成为列向量。

Y = [5 10 9 10 6]’

% 第一种计算方法

1-6*(1+0.25+0.25+1)/5/24

% 第二种计算方法

coeff = corr(X , Y , ‘type’ , ‘Spearman’)

% 等价于：

RX = [2 5 3 4 1]

RY = [1 4.5 3 4.5 2]

R = corrcoef(RX,RY)

当使用第二种计算方法计算时，所得结果如下：

由此，说明MATLAB使用的是基于第二种定义的计算方法！

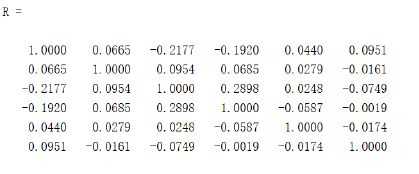
3. 皮尔逊相关系数与斯皮尔曼相关系数计算结果的对比

% 计算矩阵各列的斯皮尔曼相关系数

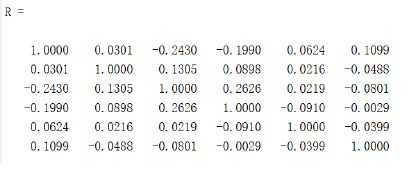
R = corr(Test, ‘type’ , ‘Spearman’)

% 计算矩阵各列的皮尔逊相关系数

R = corrcoef(Test)

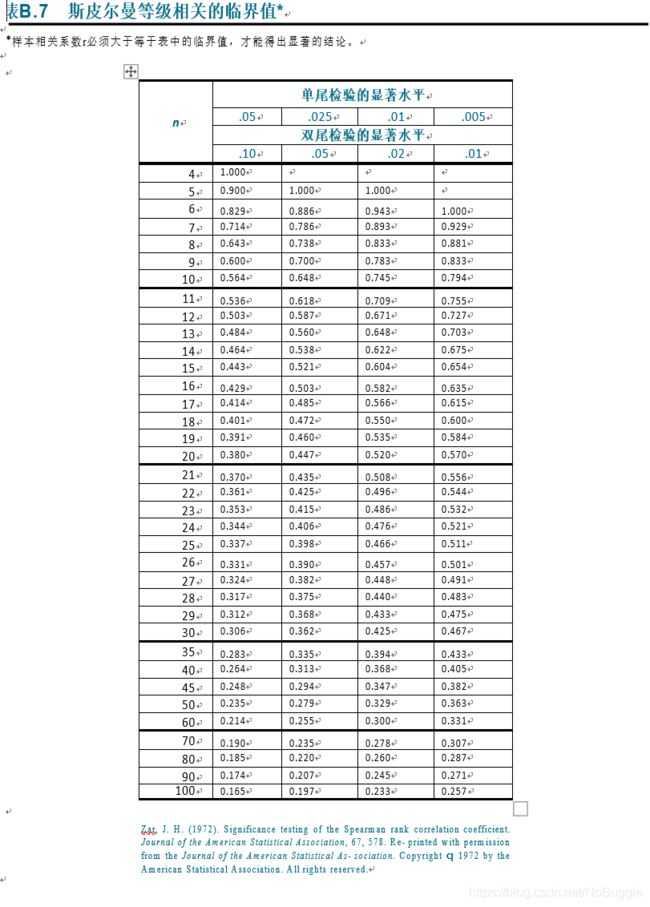
4. 斯皮尔曼相关系数的假设检验

分为两种情况：小样本和大样本

小样本情况(n ≤ 30)，直接查临界值表

H0：rs = 0； H1：rs ≠ 0

使用得出的斯皮尔曼相关系数 r 与对应的临界值进行比较。

大样本情况下，统计量

H0：rs = 0； H1：rs ≠ 0，计算检验值z*，并求出对应的p值与0.05比较即可。

% 大样本下的假设检验

% 计算检验值 z*

disp(sqrt(591-1)*0.0301)

% 计算p值

disp((1-normcdf(0.7311))*2) % normcdf用来计算标准正态分布的累积概率密度函数

% 直接给出相关系数和p值

[R,P]=corr(Test, ‘type’ , ‘Spearman’)

p > 0.05，因此无法拒绝原假设，即该相关系数和0没有显著的差异。

二、斯皮尔曼相关系数与皮尔逊相关系数的比较

连续数据，正态分布，线性关系，用皮尔逊相关系数是最巧当的，当然用斯皮尔曼相关系数也可以，只是效率没有皮尔逊相关系数高；

上述任一条件不满足，就使用斯皮尔曼相关系数，不能使用皮尔逊相关系数。

两个定序数据之间使用斯皮尔曼相关系数。

定序数据：指仅仅反映观测对象等级、顺序关系的数据，是由尺度计量形成的，表现为类别，可以进行排序，属于品质数据。

例如：优、良、差，我们可以用1表示差，2表示良、3表示优，但是，用 2 / 1 = 2 得出的 2 不具有任何含义。定序数据最重要的意义是代表了一组数据中的某种逻辑顺序。