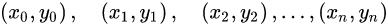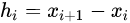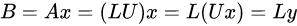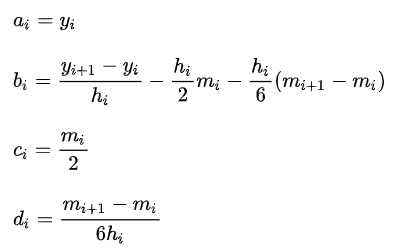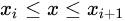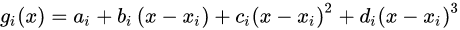如果觉得乱，可以直接看最后的【5 总结】一节。

0 英文缩写

1、经验模态分解，Empirical Mode Decomposition，EMD；

2、本征模函数，intrinsic mode function，IMF。

1 负值瞬时频率出现的原因

使用希尔伯特变换对信号数据进行处理，会得出某些负瞬时频率的原因如下：

1、分析信号中负频率出现的直接原因是两个过零点之间的多极值的结果；
2、即使没有多极值，但若具有大振幅波动也会求得负频率。

总之，瞬时频率和积分变换计算的平均频率不具有相同的物理意义，并且不具有精确的一对一对应关系。

解决方案：

通过直接正交和归一化希尔伯特变换方法，可以成功地去除负IF值。

2 三次样条插值

这里先引入三次样条插值的相关知识。

假定有n+1个数据节点：

1、计算步长：

2、将数据节点和指定的首位端点条件代入矩阵方程。

3、解矩阵方程，求得二次微分值m_i。该矩阵为三对角矩阵，常见解法为高斯消元法，可以对系数矩阵进行LU分解(见此链接的【3.1 LU分解】一节)，分解为单位下三角矩阵和上三角矩阵，即：

4、计算样条曲线的系数：

5、在每个子区间：

中，创建方程：

结束

3 IMF与EMD

再引入两个概念：非线性和非平稳过程数据的【本征模函数IMF】和【经验模态分解，即EMD方法】，其中：

1、将有具体物理解释的单分量信号称为固有模态函数，又称为本征模函数，intrinsic mode function，IMF。本征模函数IMF的两个必要条件包括：

• 在整个数据集，局部极大值与局部极小值数目之和必须与过零点的数目相等或至多相差一个；
• 在任意时间点，局部极大值所定义的上包络线与局部极小值所定义的下包络线均值为零。

2、一个实际信号可以看做是几个本征模函数的叠加，通过把一个实际信号分解为多个本征模函数，并对每一个本征模函数进行Hilbert变换，进而得到其瞬时频率，实现对实际信号的通用分析方法，即经验模态分解(Empirical Mode Decomposition，EMD)方法。EMD，即经验模态分解的步骤如下：

4 经验AM-FM分解

Hilbert-Huang Transform，HHT，希尔伯特-黄变换。HHT方法的过程：

1、首先通过对原始信号进行经验模态分解EMD，得到一定数目的能反映信号不同尺度特征的固有模态函数IMF；

2、然后对固有模态函数进行hilbert变换，得到单个信号数据的瞬时频率、瞬时相位和瞬时振幅；

3、最后对信号进行其他分析。

由于幅度和载波的频谱没有明确分开，EMD生成的IMF不能自动满足Bedrosian原理，Huang等人使用的希尔伯特变换的应用仍然受到偶然的负频率值的困扰。下面引入经验AM-FM分解，在进行分解前，首先将数据简化为IMF。下面是经验AM-FM分解的详细过程：

4.1 直接正交

采用经验AM-FM分解得到FM部分：F(t)=cos[φ(t)]，直接求其正交信号sin[φ(t)]=±√(1-F(t)²)。

4.2 归一化希尔伯特变换

采用经验AM-FM分解得到FM部分：F(t)=cos[φ(t)]，之后再进行希尔伯特变换得到正交信号后构建分析信号AS。

用经验AM-FM分解和归一化方案的方法被命名为归一化希尔伯特变换(NHT，normalization hilbert transformation)。

5 总结

通过直接正交或归一化希尔伯特变换方法，可以成功地去除负IF值。

由于这两种方法使用了经验AM-FM分解的结果，而经验AM-FM分解又需要三次样条插值，且需要首先将数据简化为IMF，因此本文的编排顺序依次见目录。

本文已将大部分所需知识进行了总结。

要厘清各节的关系，这样可能就没那么乱了。

END

今天的文章负值瞬时频率出现原因及解决方法总结分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。