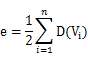图结构_左中右结构取消了吗

一、基本概念

图(Graph)：图(Graph)是一种比线性表和树更为复杂的数据结构。 

图结构：是研究数据元素之间的多对多的关系。在这种结构中，任意两个元素之间可能存在关系。即结点之间的关系可以是任意的，图中任意元素之间都可能相关。 

定义：图（Graph）是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为：G(V,E)，其中，G表示一个图，V是图G中顶点的集合，E是图G中边的集合。

二、定义及相关术语

　　图按照方向可分为有向图和无向图：

　　1、无向图

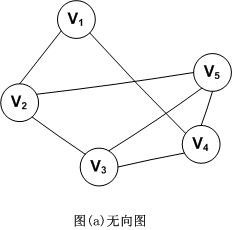
　　对于一个图，若每条边都是没有方向的，则称该图为无向图。图示如下： 

　　因此，(Vi，Vj)和(Vj，Vi)表示的是同一条边。

　　无向图的顶点集和边集分别表示为： 

　　V(G)={V1，V2，V3，V4，V5} 

　　E(G)={(V1，V2)，(V1，V4)，(V2，V3)，(V2，V5)，(V3，V4)，(V3，V5)，(V4，V5)} 

　　2、有向图

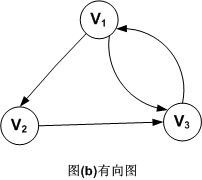
　　对于一个图G，若每条边都是有方向的，则称该图为有向图。图示如下：

　　因此，<V_i，V_j>和<V_j，V_i>是两条不同的有向边。注意，有向边又称为弧。

　　有向图的顶点集和边集分别表示为：

　　V(G)={V₁，V₂，V₃}

　　E(G)={<V₁，V₂>，<V₂，V₃>，<V_3，V₁>，<V₁，V₃>}

　　PS：无向图中的边使用小括号“()”表示，而有向图中的边使用尖括号“<>”表示。

　　3、顶点的度　　

　　　　对于无向图，顶点的度表示以该顶点作为一个端点的边的数目。比如，图(a)无向图中顶点V₃的度D(V₃)=3

　　　　对于有向图，顶点的度分为入度和出度。入度表示以该顶点为终点的入边数目，出度是以该顶点为起点的出边数目，该顶点的度等于其入度和出度之和。

　　　　比如，顶点V₁的入度ID(V₁)=1，出度OD(V₁)=2，所以D(V₁)=ID(V₁)+OD(V₁)=1+2=3

　　　　不管是无向图还是有向图，顶点数n，边数e和顶点的度数有如下关系：

　　　　因此，就拿有向图(b)来举例，由公式可以得到图G的边数e=(D(V₁)+D(V₂)+D(V₃))/2=(3+2+3)/2=4

　　4、完全图　　

　　　　完全图按照无向和有向分为无向完全图和有向完全图

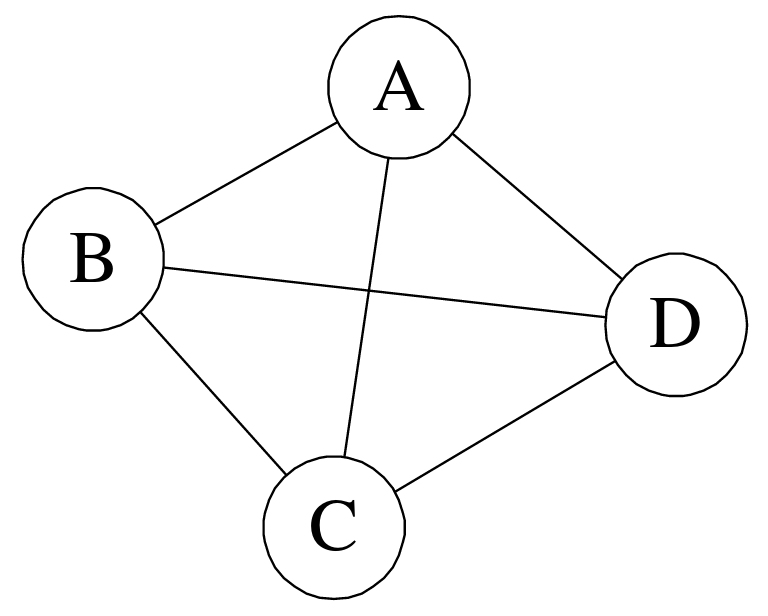
　　　　1）无向完全图：在无向图中，如果任意两个顶点之间都存在边，则称该图为无向完全图。（含有n个顶点的无向完全图有(n×(n-1))/2条边）如下图所示：

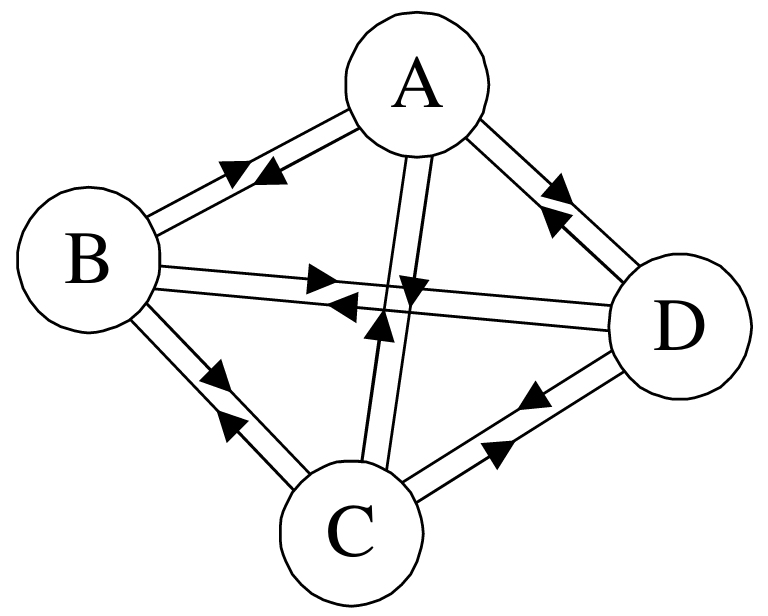
　　　　2）有向完全图：在有向图中，如果任意两个顶点之间都存在方向互为相反的两条弧，则称该图为有向完全图。（含有n个顶点的有向完全图有n×(n-1)条边）如下图所示：

　　　　PS：当一个图接近完全图时，则称它为稠密图（Dense Graph），而当一个图含有较少的边时，则称它为稀疏图（Spare Graph）。

　　5、邻接

　　　　1）若无向图中的两个顶点V1和V2存在一条边(V1,V2)，则称顶点V1和V2邻接（Adjacent）；

　　　　2）若有向图中存在一条边<V3,V2>，则称顶点V3与顶点V2邻接，且是V3邻接到V2或V2邻接到V3；

　　6、路径

　　　　在无向图中，若从顶点Vi出发有一组边可到达顶点Vj，则称顶点Vi到顶点Vj的顶点序列为从顶点Vi到顶点Vj的路径（Path）。

　　7、连通图

　　　　在无向图中，若顶点Vi到顶点Vj有路径，则称Vi和Vj是连通的。若无向图中任意两个顶点都是连通的则称该无向图为连通图，否则称为非连通图。 

　　8、权

　　　　有些图的边或弧具有与它相关的数字，这种与图的边或弧相关的数叫做权（Weight）。

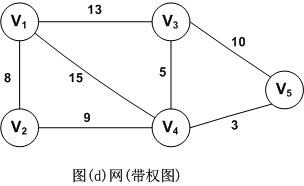
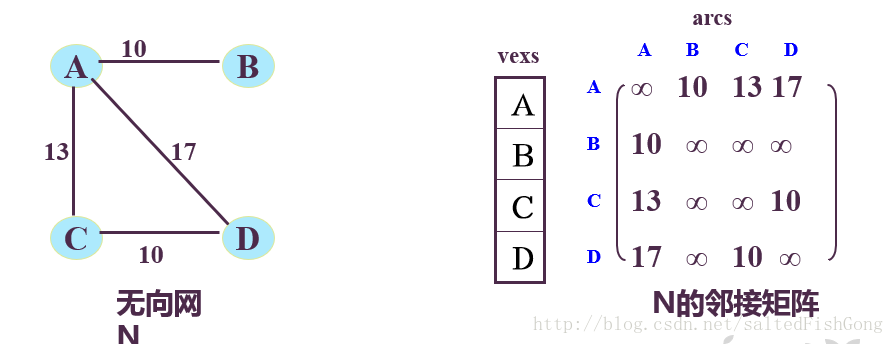
　　　　带“权值”的连通图又叫网，如图所示：

三、存储结构

　　图的2种常用的存储形式： 
　　1.数组（邻接矩阵）表示法 
　　2.邻接表表示法

　　1、数组（邻接矩阵）表示法 

　　　　用一个一维数组存放顶点的元素信息
　　　　用一个二维数组存储顶点之间的关系，其中的数据元素A[i][j] = 1,i到j有弧且i≠j,否则A[i][j]= 0

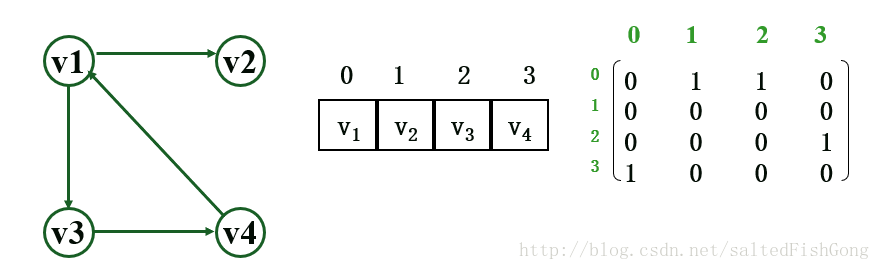
　　　　1）有向图

　　　　出度之和 = OD(vi) = 第i行元素值之和 
　　　　入度之和 = ID(vi) = 第i列元素之和

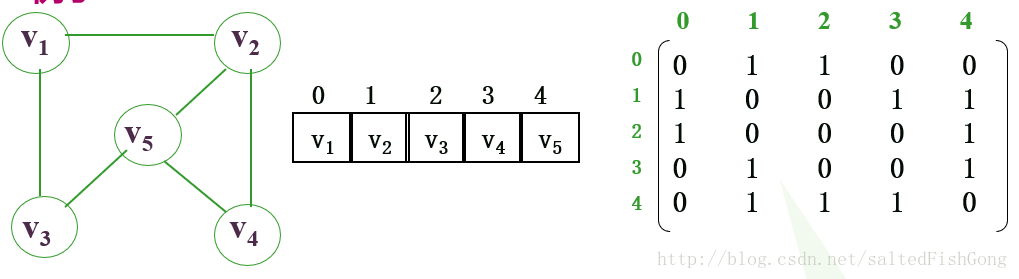
　　　　2）无向图

　　　　TD(vi) = 第i行或者第i列的元素值之和 
　　　　无向图的邻接矩阵是对称矩阵

　　　　3）网　　　　

　　　　A[i][j] = w[i][j] 若<vi,vj>或(vi,vj)∈E， 否则为∞

　　　　优点： 
　　　　　　易判定任两个顶点之间是否有边或弧存在 
　　　　　　适合存储有向图，无向图，有向网，无向网 
　　　　缺点： 
　　　　　　在边稀疏时，浪费存储空间

　　2、邻接表表示法

　　　　是图的一种链式存储结构，适用于有向图和无向图，对图中每个顶点建立一个单链表，单链表中的结点表示依附于该顶点的边（对有向图来说是以该顶点为弧尾的弧）

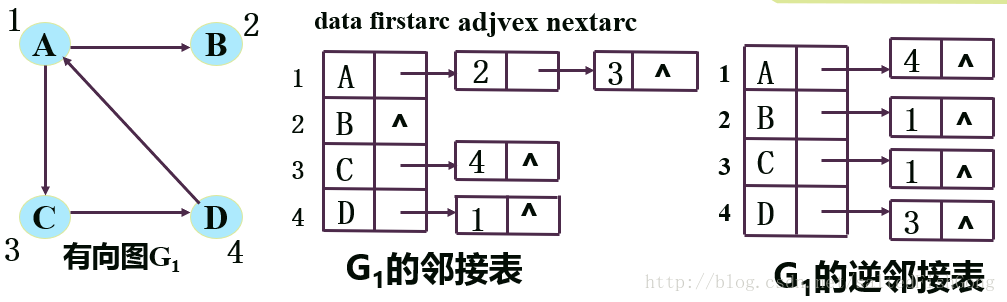
　　　　1）有向图： 
　　　　　　表结点（链式结构存储）： 
　　　　　　

　　　　　　adjvex:指示与vi邻接的顶点在图中的位置 
　　　　　　nextarc:指示下一条边或弧的结点 
　　　　　　info:存储和边或弧有关的信息(如权值)

　　　　　　头结点（顺序结构存储）： 
　　　　　　

　　　　　　data:存储顶点名称和其他相关信息 
　　　　　　firstarc:指向链表中第一个结点

　　　　　　vi的出度 = 第i个单链表中的结点数目 

　　　　　　vi的入度 = 遍历整个邻接表中其邻接点值域为i的结点个数

　　　　　　有时，为了便于确定顶点的入度或以顶点vi的弧，可以对每个顶点vi建立一个链接以vi为弧头的表——逆邻接表

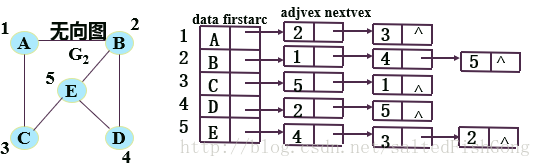
　　2）无向图

　　　　若无向图有n个顶点，e条边，则它的邻接表需要n个头结点和2e个表结点（边稀疏时比邻接矩阵省空间） 

　　　　顶点vi的度TD=第i个单链表中的结点数目，六条边用了十二个表结点——建立邻接多重表

　　　　优点：易找到任一顶点的第一个邻接点和下一个邻接点，适合存储有向图（网），无向图（网） 

　　　　缺点：难以直接判定任意两个顶点之间是否有边或者弧相连，需搜索第i和第j个单链表，不及邻接矩阵方便

　　图的另外两种不常用的存储形式：

　　3）十字链表（有向图）：

　　　　是有向图的一种存储结构，可看成有向图的邻接表与逆邻接表结合的一种链表 

　　　　头结点： 

　　　　、 
　　　　　　data:存储和顶点相关的信息 

　　　　　　firstin:指向以该顶点为弧头的第一个弧结点 

　　　　　　firstout:指向以该顶点为弧尾的第一个弧结点 

　　　　弧结点： 

　　　　、 

　　　　　　info:存储弧的相关信息 

　　　　　　tailvex:指示弧尾在图中的位置 

　　　　　　headvex:指示弧头在图中的位置 

　　　　　　hlink:指向弧头相同的下一条弧 

　　　　　　tlink:指向弧尾相同的下一条弧 

　　4）邻接多重表（无向图）：

　　　　是无向图的一种链式存储结构，每条边用一个结点表示，与邻接表表示方法的区别在于：邻接表中用两个结点表示一条边；在邻接多重表中用一个结点表示一条边 
　　　　头结点： 
　　　　、 
　　　　　　data:存储和该顶点有关的信息 

　　　　　　firstedge:指示第一条依附于该顶点的边 

　　　　边结点： 

　　　　　　mark:边结点的标志域，可用于标识该条边是否被访问过 

　　　　　　info:指向和边有关的信息的指针域 

　　　　　　ivex和jvex:为该边依附的两个顶点在图中的位置 

　　　　　　ilink:指向依附于顶点ivex的边 

　　　　　　jlink:指向依附于顶点jvex的边

　　　　　　邻接多重表各种基本操作的实现和邻接表类型 

今天的文章图结构_左中右结构取消了吗分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。