决策树原理_决策树模型是用来干嘛的

一、什么是决策树

       决策树是广泛用于分类和回归任务的模型。本质上，它从一层层的if/else问题中进行学习，并得出结论。

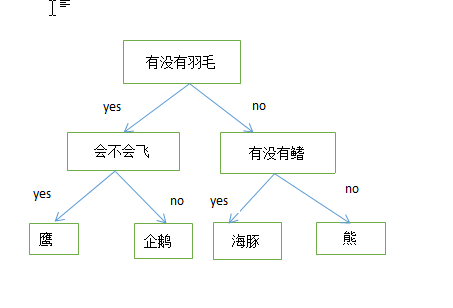
假设你要以最少的问题区分下面的四种动物：熊、鹰、海豚和企鹅，你的目标是通过提出尽可能少的问题来得到正确答案。

你可能首先会问有没有羽毛，因为鹰和企鹅有羽毛，而熊和海豚没有羽毛。接着你还可以问会不会飞来区分鹰和企鹅，有没有鳍来区分海豚和熊，

这样你就可以完美的区分这四种动物。这一系列问题生成了如下一颗树。

二、决策树的工作原理

1.决策树的结构

决策树中包含三种节点。

1)根节点(root node),它没有入边，但有零条或多条出边。

2)内部节点(internal node),恰有一条入边，和两条或多条出边。

3)叶节点(leaf node) 或者终节点(terminal node),恰有一条入边但没有出边。

2.如何构建决策树

 在构建决策树过程中时，关键问题是如何选择数据的特征属性来构建树。许多决策树的基础为Hunt算法，Hunt算法包括ID3、C4.5和CART。

 Hunt的主要思想为：

    通过将训练记录相继划分为较纯的子集，以递归的方式建立决策树。设D_t是与节点t相关联的训练记录集，而$y=\left \{ y _{1},y _{2},\cdots ,y _{k}\right \}$是类标号，Hunt算法的递归定义如下。

     (1)  如果D_t中的所有记录都属于同一个类$ y _{k}$,则t是叶子节点，用$ y _{k}$表示。

     (2) 如果D_t中包含属于多个属性的记录，则选择一个属性测试条件，将记录划分为较小的子集。对于测试条件的每个输出，创建一个子女节点，

           并根据测试结果将D_t中的记录分到子女节点中。然后对于每个子女节点，递归的调用算法。

     (3) 在(2)中所创建的子女节点可能为空，即不存在与这些节点相关联的记录。这时，该节点称为叶子节点，类标号为其父节点上训练集上的多数类。

         在上面(2)中的，如果D_t中所有记录都具有相同的特征属性，则不可能进一步划分这些记录，在这种情况下，该节点为叶子节点，

         其类标号为与该节点相关联的训练记录中的多数类。

 3.最佳划分的度量

    在决策树中，非终节点(根节点和内部节点)都包含测试条件，用于分开具有不同特性的记录。然而在训练数据集的多个特征属性，

   我们该以怎样的标准来选择特征属性来作为测试条件，考虑是通过该属性来区分后，能最大程度的区分记录，即各个数据集的纯度变得更大。

   通常有ID3、C4.5和CART三种算法：

  (1)ID3

     ID3使用的是信息增益(Infomation Gain)，信息增益代表了在一个条件下，信息复杂度（不确定性）减少的程度。

                $IG(X;Y)=H(Y)-H(Y|X)$   

     他会选择信息增益最大的特征属性作为测试条件，但是是这会带来一个缺陷，当一个特征的数值种类很多时，该特征会得到更大的增益，

      然而实际上该特征的重要性很低，这就会给分类结果造成错误。

  (2)C4.5

    信息增益率（是ID3的升级，考虑自身熵值）

    $gain ratio=\frac{IG(X;Y)}{H(X)}$

  (3)CART

     CART使用gini系数来作为衡量标准，基尼指数(基尼不纯度)：表示在样本集合中一个随机选中的样本被分错的概率。

      假设有k个类，样本点属于第 i 类的概率为$p_{i}$，则概率分布的基尼指数定义为：

      gini=$\sum_{i=1}^{k}p_{i}(1-p_{i})=1-\sum_{i=1}^{k}p_{i}^{2}$ , 其中$\sum_{i=1}^{k}p_{i}=1$

注：基尼指数和信息增益都会存在同样的问题，即数值种类比较多的特征有更大的优势作为测试条件。而信息增益率则避免这个问题。

4.控制决策树的复杂度

      通常来说，构造决策树直到所有叶节点都是纯的叶节点，这会导致模型非常复杂，并且对训练数据高度过拟合。

     常见的防止过拟合方法有两种：一种是及早停止的树的生长，叫做预剪枝；另一种是先构造树，但随后删除或折叠信息量很少的节点，也叫后剪枝。

     预剪枝的限制条件有限制树的最大深度、限制叶节点的最大数目或者规定一个节点中数据点的最小数目来防止继续划分。

     在scikit-learn中DecisionTreeRegressor类和DecisionTreeClassifier类中只实现了预剪枝，没有实现后剪枝。

     然而即使做了预剪枝，决策树也经常会过拟合，泛化性能很差。因此在大多数应用中，往往使用集成方法来代替单棵决策树。

5.树的特征重要性

    特征重要性，即每个特征对树的决策的重要性的排序。在DecisionTreeClassifier类中，他的属性feature_importance_可以获得各个特征的重要性大小。

    特征重要性的大小介于0和1之间的数字，越重要的特征，其数值越逼近1。但是实际上，如果某个特征的feature_importance_很小，

    并不能说明这个特征没有提供任何信息。这只能说明该特征没有被树选中，可能是另一个特征也包含了相同的信息。

今天的文章决策树原理_决策树模型是用来干嘛的分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。