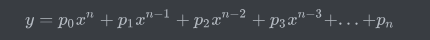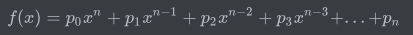多项式拟合
多项式的一般形式:
y=p_{0}x^n + p_{1}x^{n-1} + p_{2}x^{n-2} + p_{3}x^{n-3} +…+p_{n}
多项式拟合的目的是为了找到一组p0-pn,使得拟合方程尽可能的与实际样本数据相符合。
假设拟合得到的多项式如下:
f(x)=p_{0}x^n + p_{1}x^{n-1} + p_{2}x^{n-2} + p_{3}x^{n-3} +…+p_{n}
则拟合函数与真实结果的差方如下:
loss = (y_1-f(x_1))^2 + (y_2-f(x_2))^2 + … + (y_n-f(x_n))^2
那么多项式拟合的过程即为求取一组p0-pn,使得loss的值最小。
X = [x1, x2, ..., xn] - 自变量 Y = [y1, y2, ..., yn] - 实际函数值 Y'= [y1',y2',...,yn'] - 拟合函数值 P = [p0, p1, ..., pn] - 多项式函数中的系数 根据一组样本,并给出最高次幂,求出拟合系数 np.polyfit(X, Y, 最高次幂)->P
根据拟合系数与自变量求出拟合值, 由此可得拟合曲线坐标样本数据 [X, Y'] np.polyval(P, X)->Y' 多项式函数求导,根据拟合系数求出多项式函数导函数的系数 np.polyder(P)->Q 已知多项式系数Q 求多项式函数的根(与x轴交点的横坐标) xs = np.roots(Q) 两个多项式函数的差函数的系数(可以通过差函数的根求取两个曲线的交点) Q = np.polysub(P1, P2)
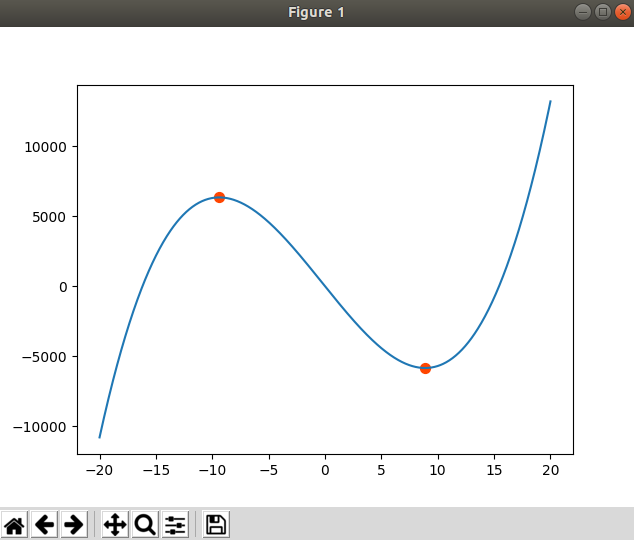
''' 1. 求出多项式的导函数 2. 求出导函数的根,若导函数的根为实数,则该点则为曲线拐点。 ''' import numpy as np import matplotlib.pyplot as mp P = [4, 3, -1000, 1] x = np.linspace(-20, 20, 1000) # y = 4*x**3 + 3*x**2 - 1000*x + 1 y = np.polyval(P, x) # 把x带入P函数 得到y # 求导 # Q = np.polyder([4,3,-1000,1]) Q = np.polyder(P) xs = np.roots(Q) # ys = 4*xs**3 + 3*xs**2 - 1000*xs + 1 ys = np.polyval(P, xs) mp.plot(x, y) mp.scatter(xs, ys, s=50, marker='o', c='orangered') mp.show()
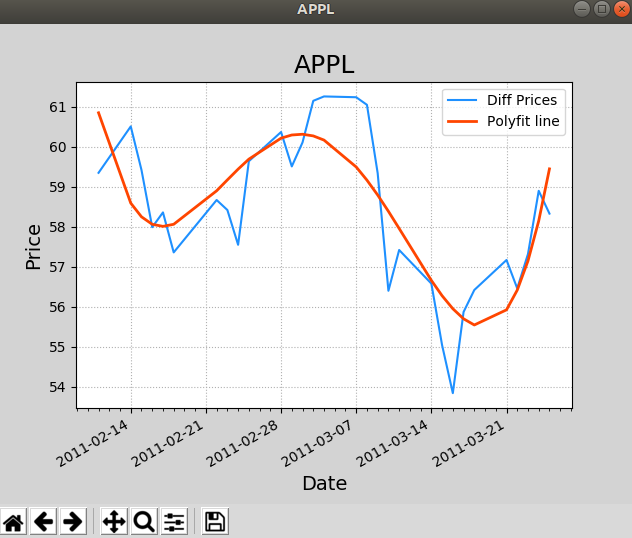
案例:使用多项式函数拟合两只股票bhp、vale的差价函数:
# 多项式拟合 import numpy as np import matplotlib.pyplot as mp import datetime as dt import matplotlib.dates as md def dmy2ymd(dmy): """ 把日月年转年月日 :param day: :return: """ dmy = str(dmy, encoding='utf-8') t = dt.datetime.strptime(dmy, '%d-%m-%Y') s = t.date().strftime('%Y-%m-%d') return s dates, bhp_closing_prices = \ np.loadtxt('bhp.csv', delimiter=',', usecols=(1, 6), unpack=True, dtype='M8[D],f8', converters={1: dmy2ymd}) # 日月年转年月日 vale_closing_prices = \ np.loadtxt('vale.csv', delimiter=',', usecols=(6,), unpack=True) # 因为日期一样,所以此处不读日期 # print(dates) # 绘制收盘价的折现图 mp.figure('APPL', facecolor='lightgray') mp.title('APPL', fontsize=18) mp.xlabel('Date', fontsize=14) mp.ylabel('Price', fontsize=14) mp.grid(linestyle=":") # 设置刻度定位器 # 每周一一个主刻度,一天一个次刻度 ax = mp.gca() ma_loc = md.WeekdayLocator(byweekday=md.MO) ax.xaxis.set_major_locator(ma_loc) ax.xaxis.set_major_formatter(md.DateFormatter('%Y-%m-%d')) ax.xaxis.set_minor_locator(md.DayLocator()) # 修改dates的dtype为md.datetime.datetiem dates = dates.astype(md.datetime.datetime) # 计算差价 diff_prices = bhp_closing_prices - vale_closing_prices mp.plot(dates, diff_prices, color='dodgerblue', label='Diff Prices') # 多项式拟合 days = dates.astype('M8[D]').astype('i4') P = np.polyfit(days, diff_prices, 4) y = np.polyval(P, days) mp.plot(dates, y, color='orangered', linewidth=2, label='Polyfit line') mp.legend() mp.gcf().autofmt_xdate() mp.show()
今天的文章多项式拟合_MATLAB多项式拟合分享到此就结束了,感谢您的阅读,如果确实帮到您,您可以动动手指转发给其他人。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/49890.html