最长上升子序列动态规划思想_算法动态规划

本文作者frankchenfu，blogs网址http://www.cnblogs.com/frankchenfu/，转载请保留此文字。

重新编辑于2020.9.2

今天我们要讲的是最长上升子序列（LIS）。

【题目描述】

给定N个数，求这N个数的最长上升子序列的长度。

【样例输入】

7

2 5 3 4 1 7 6

【样例输出】

4

什么是最长上升子序列？ 就是给你一个序列，请你在其中求出一段不断严格上升的部分，它不一定要连续。

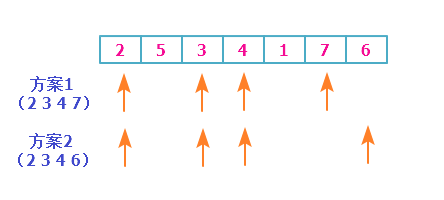
就像这样：2,3,4,7和2,3,4,6就是序列2 5 3 4 1 7 6的两种选取方案。最长的长度是4.

那么，怎么求出它的最大上升子序列长度为4呢？这里介绍两种方法，都是以动态规划为基础的。

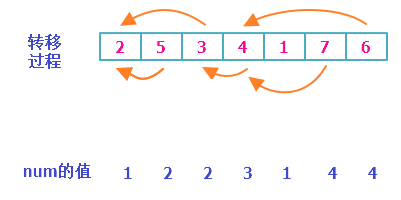
首先，我们先介绍较慢 $O(n^2)$ 的方法。我们记 $f_i$为到这个数为止，最长上升子序列的长度。

这种方法就是每一次尝试寻找“可以接下去的”那一个数，换句话说，设原序列为a，则

当$a_j<a_i (j<i)$且$f_j +1>f_i$时，$ f_i=f_j +1$。

对于每一个数，他都是在“可以接下去”的中，从前面的最优值+1转移而来。通俗的来说，你肯定就是在所有能找到的里面取最好的一个，不要白不要嘛。

因此，这个算法是可以求出正确答案的。复杂度很明显，外层i枚举每个数，内层j枚举目前i的最优值，即 $O(n^2)$。

那么，有没有更快的方法呢？当然有。这回要用到二分。

我们回想一下，在上面 $O(n^2)$ 的程序中，哪些地方看起来比较费时？

没错，就是内层用于更新i的循环。因为每一次他都要查找一遍，效率并不高。

回到题目，我们发现，他只要我们求长度，所以？

我们可以模拟一个单调栈（曾经很多参考书说这是一个栈。实际上不是严格的栈，而是一个后进入的加在末尾，然后每次可以替换掉其中元素的序列。这个序列是单调递增的，保证结果就是所求的LIS）。

所以每遇到一个比栈顶元素大的数，就放进栈里，遇到比栈顶元素小的就二分查找前边的元素，找到一个“最应该被换掉的元素”，用新数去更新前边的元素。这个元素可能不是最优解的一部分，但是它可以使得后面还未加入的、比较小的数更有可能进入这个队列。通俗地来说，作为门槛，他本来要大于当前序列的最后一个数才能加进去；就是如果我太大了，我就乖乖呆在末尾；如果前面有一个数比我大，也就是我比你好，既然我在你后面也就是我们两者只能选其一，那我只好把你替换掉了。虽然我这临时临头换的不一定最合适，但是对于后面还有很多的人等着排进来的情况下，我给他们创造了更多机会，使得这个序列的最后一个数有可能变小，让更多的人进来。

这个算法不难证明也是正确的。因为前面每一次的枚举都换成了二分，内层的复杂度从$n$降到了$log_2$，外层不变。所以总的复杂度是O($n log_2n$)。

接下来，我先给出朴素算法的代码。

#include<cstdio>
const int MAX=1001;
int a[MAX];
int lis(int x)
{
    int num[MAX];
    for(int i=0;i<x;i++)
    {
        num[i]=1;
        for(int j=0;j<i;j++)
        {
            if(a[j]<a[i]&&num[j]+1>num[i])
                   num[i]=num[j]+1;
        }
    }
    int maxx=0;
    for(int i=0;i<x;i++)
        if(maxx<num[i])
            maxx=num[i];
    return maxx;
}
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=0;i<n;i++)
        scanf("%d",&a[i]);
    return !printf("%d\n",lis(n));
}

这个则是二分算法的代码：

#include<cstdio>
#include<algorithm>
const int MAXN=200001;

int a[MAXN];
int d[MAXN];

int main()
{
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]);
    d[1]=a[1];
    int len=1;
    for(int i=2;i<=n;i++)
    {
        if(a[i]>d[len])
            d[++len]=a[i];
        else
        {
            int j=std::lower_bound(d+1,d+len+1,a[i])-d;
            d[j]=a[i]; 
        }
    }
    printf("%d\n",len);    
    return 0;
}

类似的，我们可以通过二分查找中改变“上确界”和“下确界”，以及符号（“<”和“<=”或“>”、“>=”等），求出最长不下降、不上升、严格下降子序列等问题。

希望对大家有帮助。满意请点赞！

今天的文章最长上升子序列动态规划思想_算法动态规划分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。