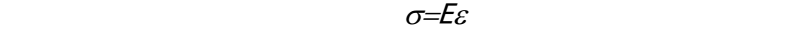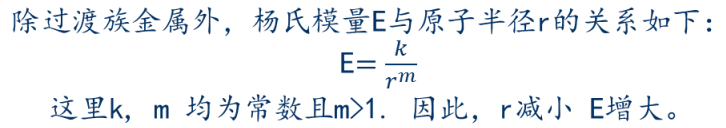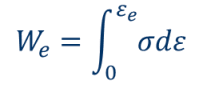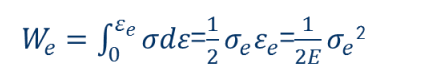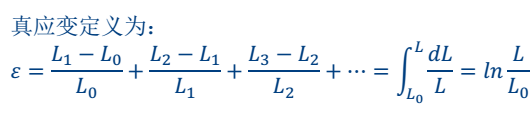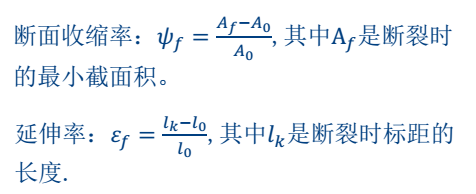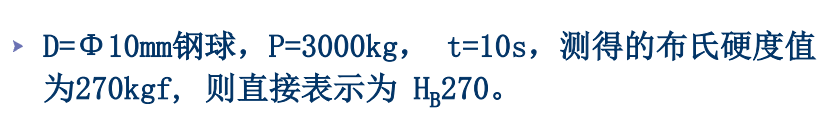材料力学性能

第一章： 绪论

一、需要掌握的概念 材料力学性能的定义、弹性变形、线弹性、滞弹性、弹性后效、弹性模量、泊松比、弹性比功、体弹性模量

二、需要重点掌握的内容 1、弹性模量的物理本质以及影响弹性模量的因素； 2、掌握根据原子间势能函数推倒简单结构材料弹性模量的方法； 3、弹性比功的计算，已知材料的应力应变曲线能求出材料卸载前和卸载后的弹性比功。

材料力学性能的定义

　　是指材料（金属和非金属等）及由其所加工成的工件在外力（拉、压、弯曲、扭转、剪切、切削等）作用下雨加工、成型、使役、实效等过程中表现出来的性能（弹塑性、强韧性、疲劳、断裂及寿命等）。 这些性能通常受到的环境（湿度、温度、压力、气氛等）的影响。

 

强度和塑性和结构材料永恒的主题！

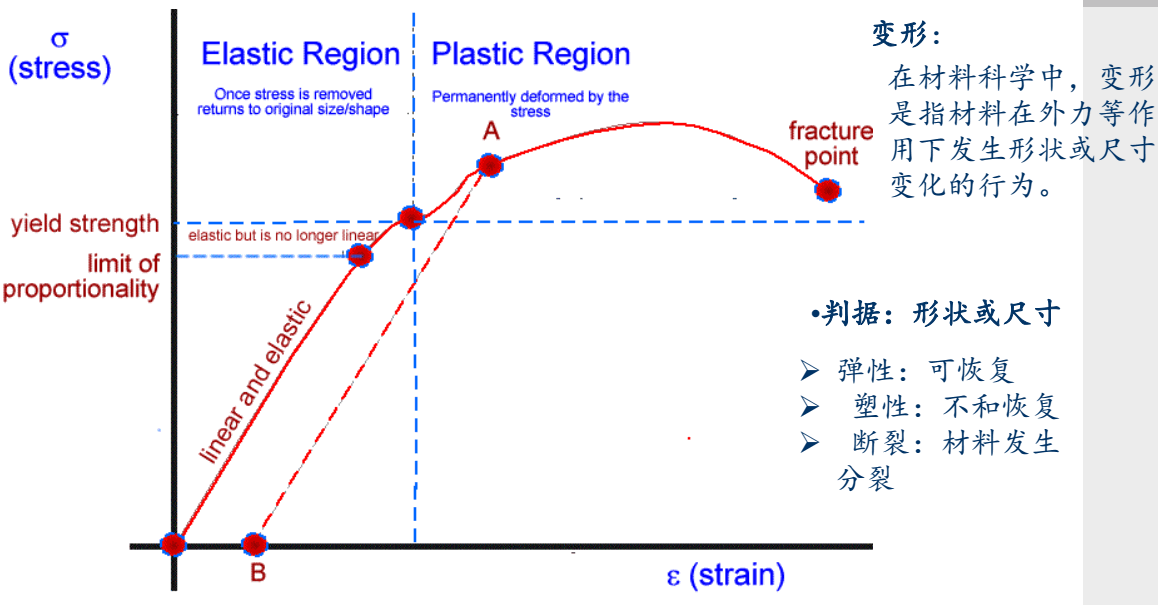
弹性变形

　　是指材料的形状和尺寸在外力去除后完全恢复原样的行为。

 

 

 

线弹性

　　是指材料的应力和应变成正比例关系。 就是上图中弹性变形里前面的一段直线部分。

 

杨氏模量（拉伸模量、弹性模量）

　　我们刚刚谈到了线弹性，在单轴拉伸的条件下，其斜率就是杨氏模量（E）。

　　它是用来衡量材料刚度的材料系数（显然杨氏模量越大，那么刚度越大）。 

 

 

杨氏模量的物理本质

　　样式模量在给定环境（如温度）和测试条件下（如应变速率）下，晶体材料的杨氏模量通常是常数。

　　 杨氏模量是原子价键强度的直接反应。 共价键结合的材料杨氏模量最高，分子键最低，金属居中。对同一晶体，其杨氏模量可能随着晶体方向的不同而不同，俗称各向异性。模量和熔点成正比例关系。

 

 

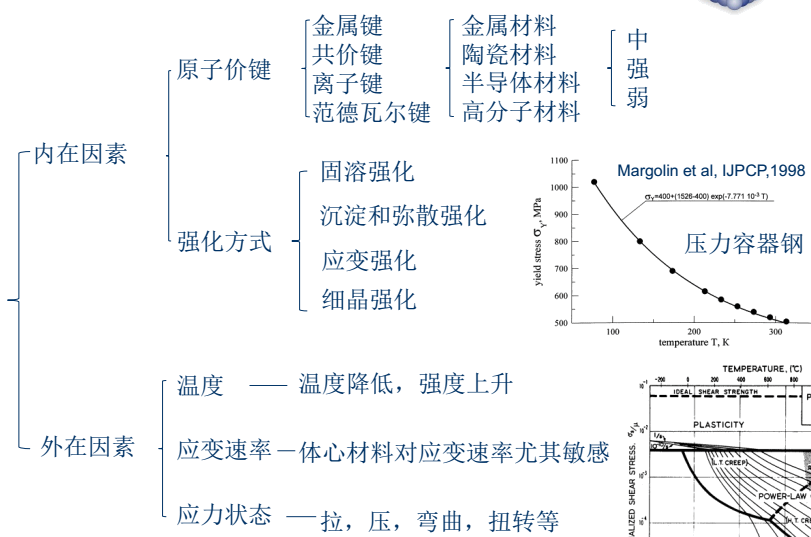
影响杨氏模量的因素

内部因素 — 原子半径

　　过渡金属的弹性模量较大，并且当d层电子数为6时模量最大。 

　　

外部因素

1. 温度：温度升高、原子间距增大，原子间的结合力减弱。 因此，通常来说， 杨氏模量随着温度的上升而下降。

2. 加载速率：工程技术中的加载速率一般不会影响金属的弹性模量。

3. 冷变形： 冷变形通常会稍稍降低金属的弹性模量，如钢在冷变形之后，其表观样式模量会下降4% – 6%。

 

泊松比

简单来说，泊松比就是单轴拉伸或压缩时材料横向应变和轴向应变比值的负数。 事实上，当材料在沿加载方向上伸长（或缩短）时，通常会在垂直于轴向方向上发生收缩（或膨胀）。 这两个量之间的比值就是泊松比。

 

关键点： 拉伸时为正值，压缩时为负值。所以：

• 一般材料的泊松比为正值，在0到0.5之间。
• 个别材料的泊松比为0，就是说他们在受压时，横向几乎没有膨胀。
• 有些材料的泊松比是赋值，他们在被拉伸变长时，同时在垂直于拉伸方向膨胀，如聚合物的泡沫。

 

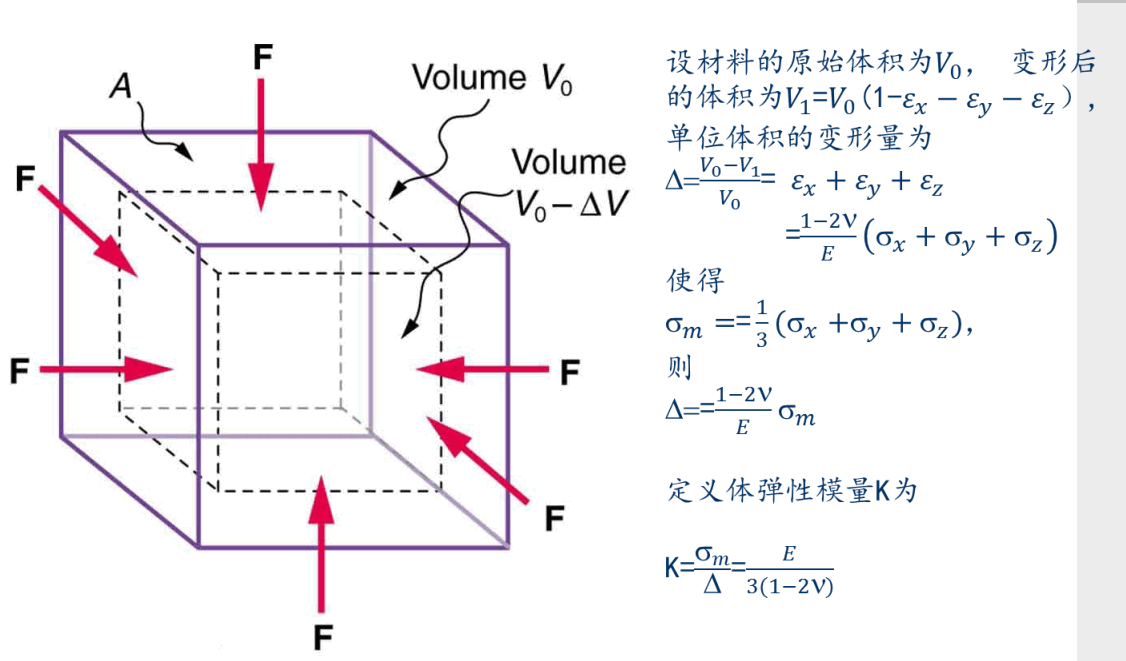
体弹性模量

只要是弹性模量，最后一定是应力/应变得到的，体弹性模量也不例外。 其中应力取得是三个方向的平均应力， 应变取的是体积的变化量（线弹性模量是应力/长度的变化量，这里是体弹性模量，自然是体积的变化量。

　

弹性比功（We）

 　　e就是elastic弹性的意思。 弹性比功又称为弹性应变能密度。它是指金属吸收变形功而又不发生永久变形（塑性变形）的能力, 是在开始塑性变形前单位体积金属所能吸收的最大弹性变形功， 是韧度指标，其数学定义如下：

　　

在线弹性条件下，上述公式可以简化为：

对于起到减震和储能的工件（如弹簧）而言，要求他们既要吸收大量的应变能，而又不允许发生塑性变形。 因此其弹性比功越大越好。

从上式可以看出，提高we的有效手段是提高弹性应力极大值。 

故具有较高的弹性极限和较小的E，从而具有较大的We，能够保证在较大的形变量下仍处于弹性变形状态。

 

 

弹性后效

完善弹性（多见于单晶材料）：将低于弹性极限的应力瞬间骤然加到材料试件上，立即产生了一个应变，在随后保持应力不变的情况下，如果应变不随着载荷保持时间变化，则为完善弹性（即在弹性范围内，应力没变，应变也不会变 ）。

 

正弹性后效（弹性蠕变）： 相同的情况下，如果应变随着时间的延长而增加并逐渐达到一个极限，这种现象称之为正弹性后效或者弹性蠕变。 

 

反弹性后效（弹性蠕变、多见于多晶材料）：　相同的情况下，骤然去除外力之后，应变瞬时回复一部分，剩余部分随着时间逐渐消失，这种现象称之为反弹性后效。　

 

 

 

滞弹性变形

滞弹性变形也是弹性弹性变形，只是其应力和应变偏离了线性关系，其程度和加载速率关系密切。　

 

 

 

 

第二章：　材料的拉伸和压缩性能

材料的拉伸性能

　　通过拉伸试验所测定的材料的性能指标统称为拉伸性能。

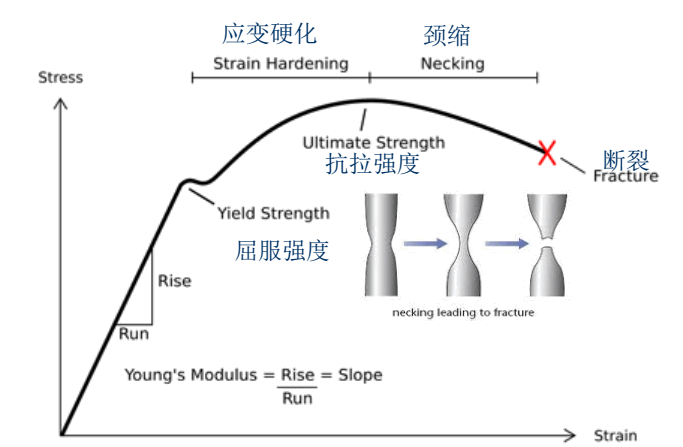
　　下面是高塑性材料的拉伸性能：

 抗拉强度很容易思考，因为超过了这一强度， 就会发生颈缩，就没有抵抗变形的能力了。

 

 

材料的屈服强度

　　屈服强度或屈服点： 定义为材料开始发生塑性变形所对应的应力。 

　　平移屈服点： 当屈服点不容易定义时， 常常通过平移法来定义屈服强度。 具体而言就是在对应于一定的应变处画一条平行于弹性部分的线。 该线和应力应变曲线的交点就是。

 

 

 

 

 

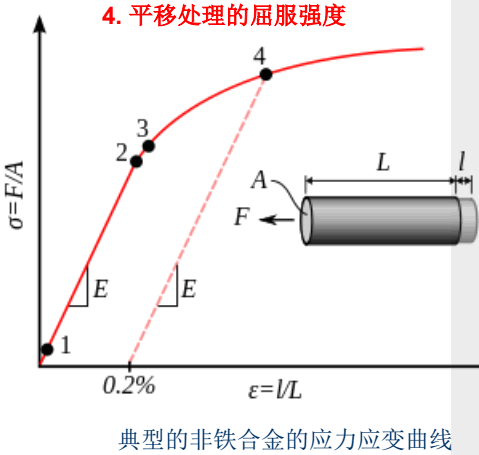
影响材料屈服强度因素

 

 

 

工程应变和真应变

　　工程应力和应变就时我们平时所说的应力和应变。而真实应力没有什么变化，但是真实应变的定义是ln的关系，如下所示：

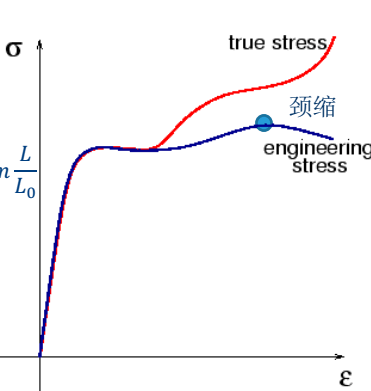
它的特点是：　在小应变条件下，　工程应力应变曲线的差别不大。如下所示：

但是真的应变可以正确的反应应变的变化趋势，且真应变是可以叠加的。

 

应变硬化（加工硬化）

　　是指材料的流变应力随着应变的增加而增加的现象。　也就是在屈服点之后上升的那一段曲线。

 

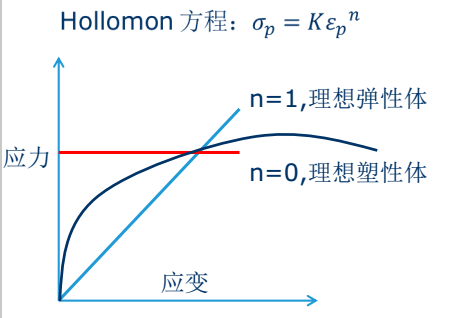
加工硬化指数在工程上的意义

 

加工硬化指数n反映了材料开始屈服后，继续变形时材料的应变硬化能力。 通常n越大，那么他抵抗局部变形的能力就越强，材料就越容易发生均匀变形。 

显然变现在应力应变曲线上时， n越大，那么加工硬化那一段的曲线就会越陡峭，说明抵抗变形的能力越大。

 

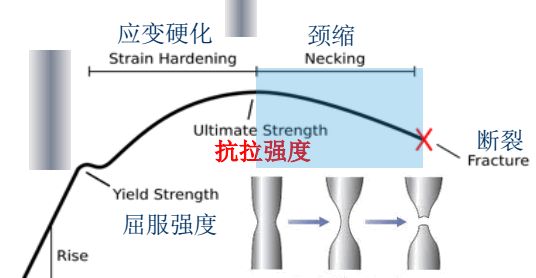
抗拉强度

　材料在拉伸条件下均匀变形时所能经受的最大应力，是材料在静拉伸条件下的最大承载力。 　

如上图所示： 拉伸强度即拉伸条件下能承受的最大应力（即曲线的最高点处对应的应力值）。

如果材料不发生颈缩，那么抗拉强度就等于断裂应力。

出现颈缩后，材料的局部受力状态从单向拉伸变成了三向拉伸。

 

 

断面收缩率与延伸率

　　

 

注意： 标距大小和延伸率是有关系的， 对于同一试样，标距越短， 那么颈缩对于总应变的贡献就越大。

 

材料拉压的不对称性

　　塑性材料在断裂时有明显的塑性变形； 而脆性材料在断裂时的变形很小。

　　脆性材料的抗压强度远远高于拉伸强度。 因此，通常情况下，脆性材料常用来制造受压零件。

 

 

包辛格效应

　　材料经过预变形之后，反向加载使得屈服强度降低甚至到零的现象。

 

 

第三章 硬度

需要重点掌握的内容： 了解5类经典的压入硬度大致测试特征，压头的形状，各自的优点和缺点，适用范围。给出特定的受试材料可以选出适宜的硬度测试方法。

首先谈一下这五种硬度是什么：

1. 布氏
2. 洛氏
3. 显微
4. 维氏
5. 纳米

硬度

　　它是物理学专业术语，材料局部抵抗硬物压入其表面的能力称为硬度。 固体是对外界物体入侵的局部抵抗能力，是比较各种材料软硬的指标。

 

谈到硬度时，我们只是谈了压入硬度，那么什么是压入硬度呢？

　　压入硬度，主要用于金属材料，方法是用一定的载荷将规定的压头压入被测材料， 以材料表面局部塑性变形的大小比较被测材料的软硬。 由于压头、载荷以及载荷持续时间的不同，压入硬度分为之前介绍的几种。

　　简单的说： 压入硬度时将压头压入金属材料，比较变形程度来规定硬度。

 

 

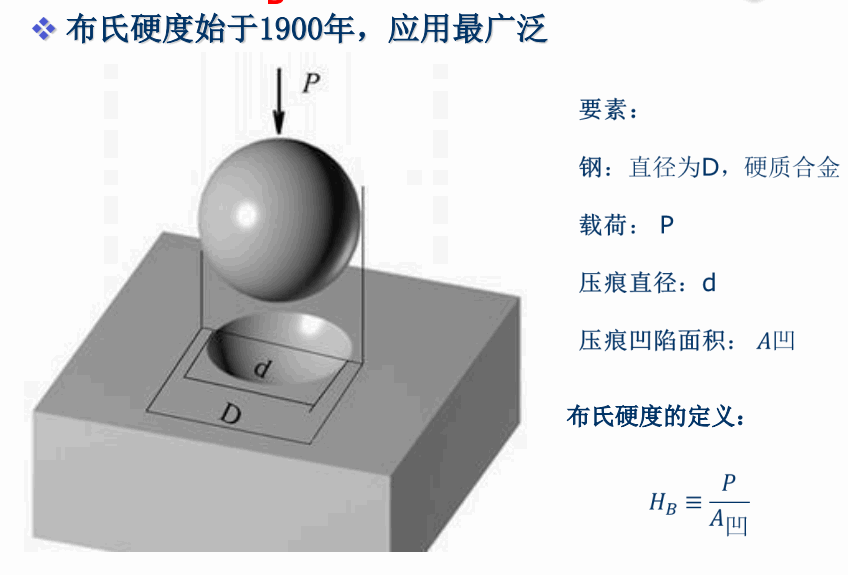
布氏硬度（H_B）

　　什么是布氏硬度? — 是用来测量硬度，第一个测量硬度的方法。

　　为什么要学习布氏硬度？ — 因为它有优点啊，所以得学，可以帮助我们衡量材料的硬度。 

　　

即布氏硬度使用钢球压入，直径为D， 载荷为P， 压入面积为A。 在生产中，我们直接规定好P和D，那么d就是唯一的变量，查表可得。

记忆： B即布氏硬度， 其中B上下有两个球，上面的就是压入的球，下面的就是压出来的球。

注意：为了使得同一材料的HB相同，我们规定 P/D2 是一个常数。

 

布氏硬度测试时，需要一定的载荷保持时间。

布氏硬度的表示方法：

即把表示硬度的标识写在前面，把值写在后面， 而一般不写单位。

 

布氏硬度的使用范围：

可以看出：优点是因为使用的压头面积比较大， 缺点是因为压力较大，损害较大。 

 

 

 

 

 

洛氏硬度

　　什么是洛氏硬度？  即一种测试硬度的方法。

　　为什么要使用洛氏硬度？ 因为布氏硬度存在缺点，洛氏硬度对之进行了改进。 　　

　　记忆： 洛氏硬度HR，R有Reform（改革）之意，即洛氏硬度是对布氏硬度的改革。

　　洛氏硬度即HR，一般又分了等级，分为HRA、HRB和HRC。 

　　显然，如果材料比较软，那么压痕就深，硬度就小；如果材料硬，那么压痕就浅，硬度就大。 

　　之前使用布氏硬度的时候，对于软的材料是不适用的，所以洛氏硬度对此必定是由改善的。

　　

 

 

维氏硬度（HV）

　　显然，前两者已经存在了，那么维氏硬度的出现一定是为了改善前两者的缺点的。在原理上，洛氏硬度已经做得不错了，所以维氏硬度沿用了相同的原理。 只是将压头修改为了136度的四方角椎体金刚石。

 

 　　所以维氏硬度相对于洛氏硬度的改进在于压头的改进。

 　　注意： 维氏硬度实验时， 实验力维持10~15s。

　　 于是可以看到维氏硬度的优点是：

• 不存在布氏硬度实验那种载荷和压头直径比例的约束。
• 不存在变形问题。
• 由于角锥压痕轮廓清晰，采用对角线长度计量， 精确可靠。
• 不存在洛氏硬度的硬度级无法统一的缺点，而且较洛氏硬度能够更好的测量极薄试样的硬度。 

 　　当然， 他也是存在缺点的：

• 硬度值需要使用对角线来测量，然后查表获得，所以生产效率不如洛氏硬度，不适合大批量的常规检验。　　

 

 

显微硬度

　　既然维氏硬度已经很好的解决大部分问题了，那么显微硬度的出现是为了什么呢？ 为了小、薄样品或组织而生。

　　因为前面几种测量硬度的方法都是适合于宏观上的金属的硬度测量，但是对于其中的组织等的测量却非常不准确。

　　显微硬度的原理类似于维氏硬度。 它的主要特征是载荷小并且使用了小型化的维氏压头和努氏压头。

 

 

努氏硬度

　　

 

 

 

几种硬度方法的比较

 

 

 

第四章 材料的断裂及端口分析

断裂

　　断裂是指材料在外力的作用下分裂成两片或更多片的行为，它是机械和工程构件发生实效的主要形式之一。

　　研究断裂的主要目的是防止断裂，以保证构件在服役过程中的安全。

　

脆性断裂的宏观特征

• 断裂前不发生塑性变形。
• 裂纹的扩展速度往往很快，接近音速。
• 断裂前没有明显的征兆可寻，且断裂时突然发生的， 因而往往引起严重的后果。

　　所以： 要特别注意防止脆断。

 

韧断端口特征

 

脆断端口特征

　　

 

 

穿晶断裂和沿晶断裂

　　

可以看出，穿晶断裂时穿过晶体的内部，而沿晶断裂时沿着晶体的边缘发生的断裂。

注意：微量元素可以剧烈的影响材料的塑性与变形机制。

 

 

解理断裂

　　解理断裂是在正应力作用产生的一种穿晶断裂，即断裂面沿一定的晶面（即解理面）分离。解理断裂常见于体心立方和密排六方金属及合金，低温、冲击载荷和应力集中常促使解理断裂的发生。面心立方金属很少发生解理断裂。解理断裂通常是宏观脆性断裂，它的裂纹发展十分迅速，常常造成零件或构件灾难性的总崩溃。解理断裂的电子图象，具有河流花样，河流花样变化处为小角度倾斜晶界。

　　

 

 

四大强度理论

　　

 

 

传统安全设计准则

 

裂纹体力学的诞生

　　有时虽然工作应力远低于材料屈服强度时也会发生所谓的低应力脆断的现象。 因为传统力学把材料看成是均匀的，没有缺陷的， 没有裂纹的理想固体，但是实际的工程材料， 在制备。。。过程中， 都会产生各种宏观缺陷乃至宏观裂纹。

 

于是实际断裂强度<<理论断裂强度的原因是： 材料内部存在有裂纹。

• 玻璃： 结晶后，由于热应力产生固有的裂纹。 
• 陶瓷： 粉末在压制烧结时也不可避免的残存裂纹。
• 金属： 没有裂纹？

当金属在塑性变形不均匀，当变形受到阻碍（如晶界、第二相等）产生了很大的应力集中，当应力集中达到了理论断裂强度，而材料又不能通过塑性变形使得应力松弛时， 这样就开始萌生裂纹。

 

格里菲斯断裂理论

　　

 

 

 

 

 

 

缺口

　　缺口会造成应力集中。 

 

应力集中系数

　　

热疲劳

　　由于温度周期变化而引起零件或构件的膨胀和收缩，而又因为这种膨胀和收缩受到约束，产生了交变热应力， 由这种交变热应力引起的材料性能的改变就是热疲劳。

 

热疲劳破坏

　　由于热疲劳而引起的材料或工件的失效或者断裂，称为热疲劳破坏。

 

 

提高疲劳强度的途径

　　使材料或工件表面产生很高的压应力， 表面处理： 滚压，喷丸和渗氮。

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

　　

 

 

 

 

　　

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

over

今天的文章材料力学性能分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。