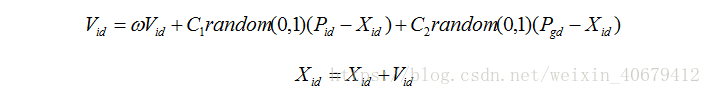粒子群优化算法pso_pso粒子群算法

1、粒子群优化算法（Partical Swarm Optimization PSO），粒子群中的每一个粒子都代表一个问题的可能解，

通过粒子个体的简单行为，群体内的信息交互实现问题求解的智能性。

2、粒子群算法最早是由Eberhart和Kennedy于1995年提出，它的基本概念源于对鸟群觅食行为的研究。设想这样一个场景：一群鸟在随机搜寻食物，在这个区域里只有一块食物，所有的鸟都不知道食物在哪里，但是它们知道当前的位置离食物还有多远。最简单有效的策略？寻找鸟群中离食物最近的个体来进行搜素。PSO算法就从这种生物种群行为特性中得到启发并用于求解优化问题。

用一种粒子来模拟上述的鸟类个体，每个粒子可视为N维搜索空间中的一个搜索个体，粒子的当前位置即为对应优化问题的一个候选解，粒子的飞行过程即为该个体的搜索过程．粒子的飞行速度可根据粒子历史最优位置和种群历史最优位置进行动态调整．粒子仅具有两个属性：速度和位置，速度代表移动的快慢，位置代表移动的方向。每个粒子单独搜寻的最优解叫做个体极值，粒子群中最优的个体极值作为当前全局最优解。不断迭代，更新速度和位置。最终得到满足终止条件的最优解。

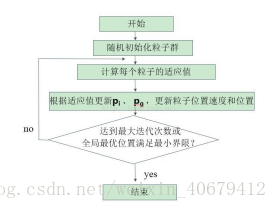
3、算法流程如下：

  1、初始化

首先，我们设置最大迭代次数，目标函数的自变量个数，粒子的最大速度，位置信息为整个搜索空间，我们在速度区间和搜索空间上随机初始化速度和位置，设置粒子群规模为M，每个粒子随机初始化一个飞翔速度。

 2、 个体极值与全局最优解

定义适应度函数，个体极值为每个粒子找到的最优解，从这些最优解找到一个全局值，叫做本次全局最优解。与历史全局最优比较，进行更新。

 3、 更新速度和位置的公式

 4、 终止条件

（1）达到设定迭代次数；（2）代数之间的差值满足最小界限

以上就是最基本的一个标准PSO算法流程。和其它群智能算法一样，PSO算法在优化过程中，种群的多样性和算法的收敛速度之间始终存在着矛盾．对标准PSO算法的改进，无论是参数的选取、小生境技术的采用或是其他技术与PSO的融合，其目的都是希望在加强算法局部搜索能力的同时，保持种群的多样性，防止算法在快速收敛的同时出现早熟收敛。

4、

首先总结一下PSO算法的一些优点：（1）它是一类不确定算法。不确定性体现了自然界生物的生物机制，并且在求解某些特定问题方面优于确定性算法。（2）是一类概率型的全局优化算法。非确定算法的优点在于算法能有更多机会求解全局最优解。（3）不依赖于优化问题本身的严格数学性质。（4）是一种基于多个智能体的仿生优化算法。粒子群算法中的各个智能体之间通过相互协作来更好的适应环境，表现出与环境交互的能力.（5）具有本质并行性。包括内在并行性和内含并行性。（6）具有突出性。粒子群算法总目标的完成是在多个智能体个体行为的运动过程中突现出来的。（7）具有自组织和进化性以及记忆功能，所有粒子都保存优解的相关知识。（8）都具有稳健性。稳健性是指在不同条件和环境下算法的实用性和有效性，但是现在粒子群算法的数学理论基础还不够牢固，算法的收敛性还需要讨论。

从中可以看出PSO具有很大的发展价值和发展空间，算法能够用于多个领域并创造价值，在群智能算法中具有重要的地位，同时也能够在相关产业创造价值，发挥作用。下面结合相关产业具体分析一下。

计算智能的算法，往往结合大数据平台，包括GPU运算，并行计算，HPC，多模式结合等手段，来完成更加复杂多变的业务需求。

下面具体分析在产业中的作用（1）模式识别和图像处理。PSO算法已在图像分割、图像配准、图像融合、图像识别、图像压缩和图像合成等方面发挥作用。（2）神经网络训练。PSO算法可完成人工神经网络中的连接权值的训练、结构设计、学习规则调整、特征选择、连接权值的初始化和规则提取等。但是速度没有梯度下降优化的好，需要较大的计算资源。一般都算不动。（3）电力系统设计，例如：日本的Fuji电力公司的研究人员将电力企业某个著名的RPVC(Reactive Power and Voltage Control)问题简化为函数的最小值问题，并使用改进的PSO算法进行优化求解。（4）半导体器件综合，半导体器件综合是在给定的搜索空间内根据期望得到的器件特性来得到相应的设计参数。（5）还有其他的一些相关产业。包括自动目标检测、生物信号识别、决策调度、系统识别以及游戏训练等方面也取得了一定的研究成果。

5、

clc
clear 
close all
E=0.000001;
maxnum=800;%最大迭代次数
narvs=2;%目标函数的自变量个数
particlesize=50;%粒子群规模
c1=2;%每个粒子的个体学习因子，加速度常数
c2=2;%每个粒子的社会学习因子，加速度常数
w=0.6;%惯性因子
vmax=5;%粒子的最大飞翔速度
v=2*rand(particlesize,narvs);%粒子飞翔速度
x=-300+600*rand(particlesize,narvs);%粒子所在位置
%定义适应度函数
fitness=inline('(x(1)^2+x(2)^2)/10000','x');
for i=1:particlesize
    f(i)=fitness(x(i,:));    
end
personalbest_x=x;
personalbest_faval=f;
[globalbest_faval,i]=min(personalbest_faval);
globalbest_x=personalbest_x(i,:); 
k=1;
while (k<=maxnum)
    for i=1:particlesize
            f(i)=fitness(x(i,:));
        if f(i)<personalbest_faval(i)
            personalbest_faval(i)=f(i);
            personalbest_x(i,:)=x(i,:);
        end
    end
    [globalbest_faval,i]=min(personalbest_faval);
    globalbest_x=personalbest_x(i,:);
    for i=1:particlesize
        v(i,:)=w*v(i,:)+c1*rand*(personalbest_x(i,:)-x(i,:))...
            +c2*rand*(globalbest_x-x(i,:));
        for j=1:narvs
            if v(i,j)>vmax
                v(i,j)=vmax;
            elseif v(i,j)<-vmax
                v(i,j)=-vmax;
            end
        end
        x(i,:)=x(i,:)+v(i,:);
    end
    ff(k)=globalbest_faval;
    if globalbest_faval<E
        break
    end
%       figure(1)
%       for i= 1:particlesize
%       plot(x(i,1),x(i,2),'*')
%       end
    k=k+1;
end
xbest=globalbest_x;
figure(2)
set(gcf,'color','white');
plot(1:length(ff),ff)

原文：https://blog.csdn.net/weixin_40679412/article/details/80571854

今天的文章粒子群优化算法pso_pso粒子群算法分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。