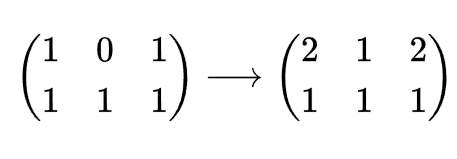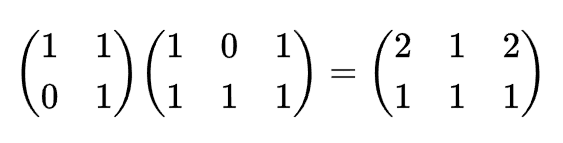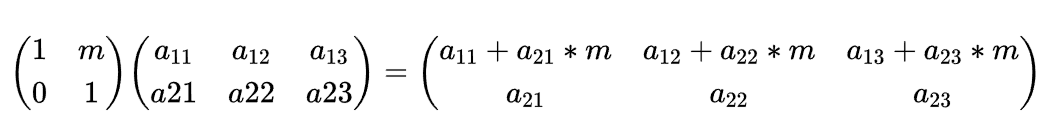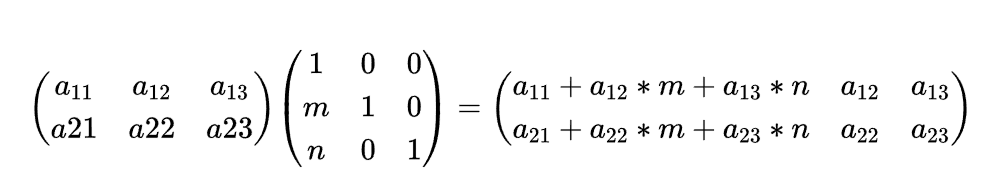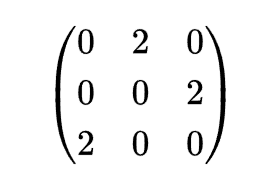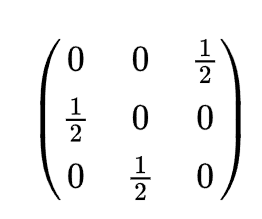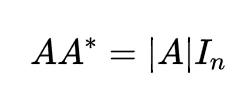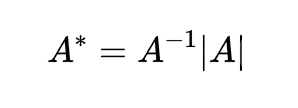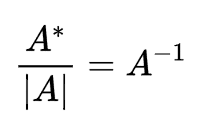一.初等矩阵

　　将单位阵E经过一次变换得到的矩阵称为初等矩阵。初等矩阵都是方阵。这种初等变换有某一行（列）的n倍加到另一行（列）上、互换行列位置、某一行（列）全部乘以某实数三种基本情况。

　　每一个初等矩阵都可以写作单位阵左乘或右乘一个矩阵的形式。初等行变换是左乘，初等列变换时右乘，下面以2×3矩阵为例说明行变换对应左乘，列变换对应右乘：

　　这个变换是将第二行乘以1加到第一行上，相当于左乘一个矩阵，这个矩阵是由单位阵变换而来，同样是将单位阵的第二行乘以1加到第一行上得到。我们可以将这个过程一般化表示：

　　这是将第二行乘以m加到第一行上的行变换的一般化表示。对于初等列变换同样地（只是变成了右乘相应的方阵），如将第二列和第三列都加到第一列上：

　　结合矩阵的意义可以知道，矩阵的乘法对应了空间变换的复合，因此对矩阵应用初等行列变换相当于矩阵的对应空间也在变换。一般地，我们将矩阵视作列向量的组合，相应的计算矩阵对应空间的变换的复合时使用的是左乘，自然对应的矩阵变换就是行变换。

　　对于两个矩阵A和B，如果A能经过初等变换得到B，那么就称为A和B等价。怎么理解这种等价关系呢？我们初等变换有3种方式：交换两行（列）、某一行（列）乘以实数n、将一行（列）乘以实数m然后加到另一行（列）上，而我们会发现行列式中也有这三种运算，而且行列式中这三种变换也只会将行列式的值改变为原来的n倍，如交换两行（列），行列式的值变为原来的-1倍，所以行列式的值如果不为0的话，那么经过这些变换后行列式值仍然不为0。因此我们可以大胆估计，初等变换并不会改变矩阵的秩（方阵对应行列式不为0，方阵的秩等于阶数），实际上也正是如此（不做证明）。

　　单位阵都是满秩的，因此单位阵经过初等变换后得到的初等矩阵也是满秩的。所以这里我们可以这样理解等价关系：矩阵A和B等价意味着这两个矩阵行列数相同以及秩相等。其实这里说的等价只是一种弱等价关系，这种只有秩相等的两个矩阵的关系可以称为相抵关系。

二.初等矩阵用于求逆矩阵

　　1.逆矩阵

　　　　什么是逆矩阵？我们知道矩阵对应着相应的空间变换，这种空间变换有旋转、拉伸和投影三种形式，那么我们以下面两个矩阵为例说明逆矩阵：

　　　　可以看到，第一个矩阵对应的变换是绕着向量（1，1，1）所在直线旋转90度并拉伸三个坐标的长度为原来的两倍，第二个矩阵同样是绕着向量（1，1，1）所在直线旋转90度，只是旋转方向和第一个矩阵相反，同时三个坐标的长度压缩为原来的一半。很容易发现，这两个矩阵对应的变换是完全相反的，这样的两个矩阵就互为逆矩阵（指对应空间变换完全相反）。既然对应的空间变换完全相反，那么复合这两种空间变换得到的新的空间就和原来空间相同，也就是这两个矩阵的乘积（不论谁在左谁在右）为单位阵（这里不再验证了）。

　　2.用初等变换求逆矩阵

　　　　初等行变换对应着空间变换，因此我们可以用初等行变换记录空间变换的过程。既然逆矩阵是和原矩阵变换方向完全相反的矩阵，那么我们将原矩阵对应的空间还原回去，并使用初等行变换记录还原的过程得到的矩阵不就是相应的逆矩阵吗？因此便有了以下求逆矩阵的方法：

　　　　将要求逆矩阵的矩阵右边增广一个方阵，然后对左边矩阵应用初等行变换使它变换为方阵，右边的方阵跟随左边矩阵应用相同变换。左边矩阵变换为方阵的过程就是将这个矩阵对应的空间反向变换为原始的空间，而右边的方阵的跟随变换相当于记录了这个逆向变换的过程，这个记录的结果就是原来矩阵的逆矩阵。

　　3.利用伴随阵求逆矩阵

　　　　伴随矩阵是用于求逆矩阵的一种构造矩阵。它的结构如下图（图片来源于百度）：

　　　　为什么这么构造呢？根据行列式性质，行列式可以按照某一行（列）展开，展开后的结果就是这一行（列）的每个元素乘以其对应的代数余子式的总和。所以我们的构造方法是将原来方阵写成对应的行列式，然后求所有元素的代数余子式按照原来方式排列后再转置。经过转置后，根据矩阵左行乘右列的性质，如果A右乘A*，那么结果矩阵的元素就等于A的行乘上A*的列，以A的第一行乘以A*的列为例，根据行列式的规则，只有乘上A*的第一列的结果就是A的行列式值，而乘以其他列的结果都为0。同理，A的其他行乘上A*的列的结果就如下所示：

　　　　显然这个行列式等于单位阵乘以|A|。也就有了以下的公式：

　　　　其中I_n是n阶单位阵。由于A和A^-1的结果为单位阵，因此公式两边同时左乘A^-1，就得到了如下公式：

　　　　当|A|不为0时也就有：

　　　　这就是使用伴随矩阵求逆矩阵的公式。

　　4.方阵可逆

　　　　根据上一小节中根据矩阵的伴随阵求逆矩阵的公式推导过程可知，当方阵对应行列式值不为0时矩阵有逆矩阵。这也很容易理解，当方阵对应行列式值为0时，方阵的秩小于阶数，这意味着经过方阵对应的空间变换后，空间的维度会减小，从高维变为低维，但是当从低维反向变换回高维时就会出现问题，因为高维空间投影到低维空间的变换是n对一，也就是说高维空间中有无数条向量映射到低维空间中是同一条向量，因此从低维空间反向投影到高维空间是不可行的，所以像这样不满秩的方阵也就没有逆矩阵，也称为不可逆。

今天的文章线性代数总结记录五：逆矩阵分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。