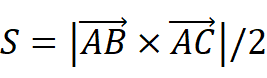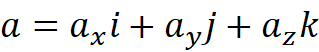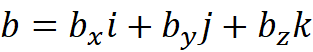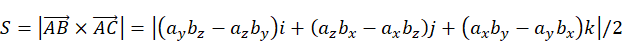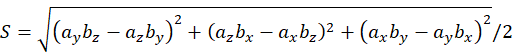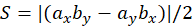向量积计算三角形面积

向量积：数学中又称外积、叉积，物理中称矢积、叉乘，是一种在向量空间中向量的二元运算。

向量积可以被定义为：

模长：（在这里θ表示两向量之间的夹角（共起点的前提下）（0°≤θ≤180°），它位于这两个矢量所定义的平面上。）

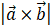
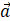
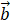
向量积的模（长度）在数值上等于，，及其夹角θ组成的平行四边形的面积。所以求三角形ABC的面积，根据向量积的意义，可得三角形ABC的面积S：

a×b=(aybz-azby)i+(azbx-axbz)j+(axby-aybx)k,为了帮助记忆，利用三阶行列式，写成：

其中i，j，k是三个相互垂直的单位向量。它们刚好可以构成一个坐标系。

这三个向量的特例就是i=（1，0，0），j=（0，1，0），k=（0，0，1）。

即：

tips：空间向量(x,y,z)，其中x,y,z分别是三轴上的坐标，模长是

即：

因为是二维三角形，所以az，bz=0，所以：

今天的文章向量积计算三角形面积分享到此就结束了，感谢您的阅读。