首先介绍一下ode45的格式:
[t,y] = ode45(odefun,tspan,y0)[t,y] = ode45(odefun,tspan,y0,options)[t,y,te,ye,ie] = ode45(odefun,tspan,y0,options)sol = ode45(___)
这里介绍一阶微分方程:
[自变量,因变量] = ode45(方程,范围,初值);
举个栗子:
首先创建一个func2.m函数存放方程表达式
function Biubiu = func2(h, t) g = 9.8; Biubiu = (10000*pi/sqrt(2*g))*(h.^(3/2) - 2*(h.^(1/2))); end
接着在MATLAB命令窗口输入:
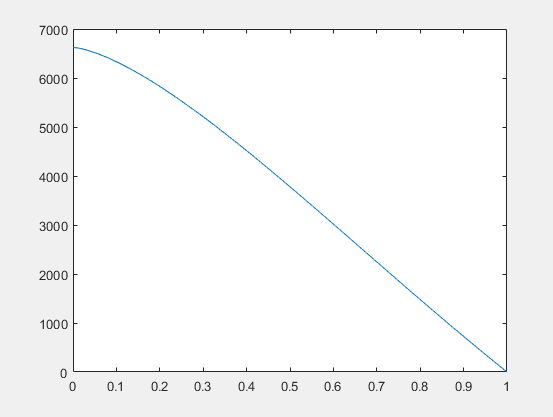
tspan = [1 0];%函数范围 t_1 = 0;%初值 [h,t] = ode45(@func2, hspan, t_1); plot(h,t);%绘图
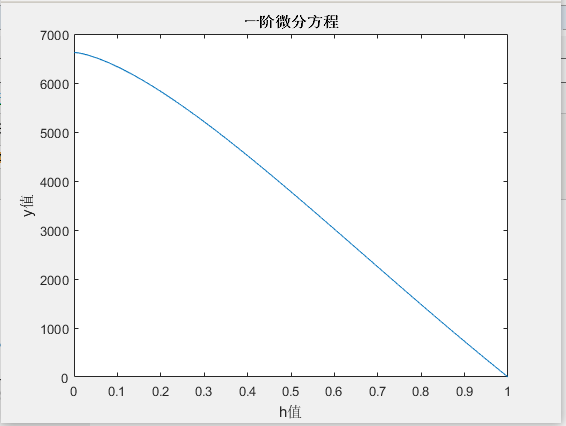
可以丰富一下图像,增加横坐标名,纵坐标名和标题
xlabel('h值')
ylabel('y值')
title('一阶微分方程')
相关资料访问:https://ww2.mathworks.cn/help/matlab/ref/ode45.html?s_tid=doc_ta
今天的文章ode45求解微分方程(MATLAB)分享到此就结束了,感谢您的阅读,如果确实帮到您,您可以动动手指转发给其他人。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/55515.html