频域分析相关概念

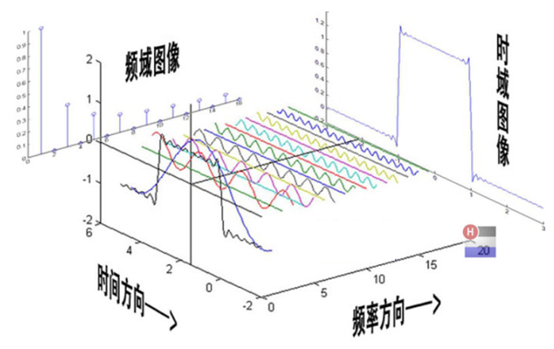
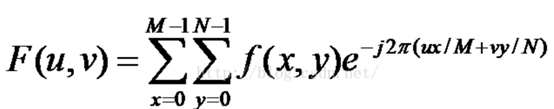时域，频域，空间域

时域：时域是描述数学函数或物理信号对时间的关系。例如一个信号的时域波形可以表达信号随着时间的变化。(以时间作为变量所进行的研究)

频域（频率域）：横轴是频率,纵轴是该频率信号的幅度,也就是通常说的频谱图。频谱图描述了信号的频率结构及频率与该频率信号幅度的关系。(以频率作为变量所进行的研究)

空间域：空间域又称图像空间。由图像像元组成的空间。在图像空间中以长度(距离)为自变量直接对像元值进行处理称为空间域处理。(以空间坐标作为变量所进行的研究)

将图像变换到另一种域中，可能会有利于进行处理和计算——频域分析的作用，换个更容易看清楚的角度看信号。

傅里叶变换：

傅里叶变换的作用：傅立叶变换是将图像从空间域转换到频率域，其逆变换是将图像从频率域转换到空间域。换句话说，傅立叶变换的物理意义是将图像的灰度分布函数变换为图像的频率分布函数，傅立叶逆变换是将图像的频率分布函数变换为灰度分布函数。

离散傅里叶变换（DFT）：

傅里叶变换后图像的形成：

图像的傅立叶变换将图像分解，频率空间具有二维，对于x和y维中的波的频率 h和k。因此，它不是以一系列尖峰的形式绘制的，而是以与原始图像（大约）相同的像素尺寸绘制的图像。傅立叶变换中的每个像素都有一个坐标（h，k）表示在傅立叶变换中具有x频率h和 y频率k的正弦波的贡献。

图像也可以看成正弦波的总和：

将图像视为二维函数，在灰度值图像中，像素值的范围是0到255，代表该点的明暗程度。

二维中，将图像的明暗程度视为水平和垂直坐标的函数，给出了该像素点的位置。所以，可以将图像视为起伏的景观，而高度由像素值确定。

图像高频低频含义

图像的频率是表征图像中灰度变化剧烈程度的指标，是灰度在平面空间上的梯度。

简短概括：

图像的高频，意味着灰度变化剧烈

图像的低频，意味着灰度变化平坦

不同频率信息在图像结构中有不同的作用：

图像的主要成分是低频信息，它形成了图像的基本灰度等级，对图像结构的决定作用较小；

中频信息决定了图像的基本结构，形成了图像的主要边缘结构；

高频信息形成了图像的边缘和细节，是在中频信息上对图像内容的进一步强化。

今天的文章频域分析相关概念分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。